1911 Encyclopædia Britannica/Steam Engine

←

Steam

1911 Encyclopædia Britannica, Volume 25

Steam Engine by James Alfred Ewing

Steamship Lines

→

sister projects: Wikipedia article, quotes, travel guide, Wikidata item

See also Steam engine on Wikipedia; and our 1911 Encyclopædia Britannica disclaimer.

24509781911 Encyclopædia Britannica, Volume 25 — Steam EngineJames Alfred Ewing

STEAM ENGINE, 1. A steam engine is a machine for the conversion of heat into mechanical work, in which the working substance is water and water vapour. The working substance may be regarded from two points of view. Thermodynamically it is the vehicle by which heat is conveyed to and through the engine from the hot source (the furnace and boiler). Part of this heat suffers a transformation into work as it passes through, and the remainder is rejected, still in the form of heat. Mechanically the working substance is a medium capable of exerting pressure, which effects this transformation in doing work by means of the changes of volume which it undergoes in the operation of the machine. Regarded as a thermodynamic device, the function of the engine is to get as much work as possible from a given quantity of heat or, to go a step further back, from the combustion of a given quantity of fuel. Accordingly, a question of primary importance is what is called the efficiency of the engine, which is the ratio of the work done to the heat supplied. Before, however, proceeding to discuss the steam engine in this aspect, or treating of the mechanics of its modern forms, it may be useful to give a brief historical sketch of its early development as an industrial appliance. In any such sketch the chief share of attention must necessarily be given to the work of James Watt. But a process of evolution had been going on before the time of Watt which prepared the steam engine for the immense improvements it received at his hands. His labours stand in natural sequence to those of Thomas Newcomen, and Newcomen’s to those of Denis Papin and Thomas Savery. Savery’s engine in its turn was the reduction to practical form of a contrivance which had long before been known as a scientific toy. The most modern type of all, the steam turbine of C. A. Parsons, is a new departure which has but little to connect it directly with the past; but even the steam turbine not only profits by the inventions of Watt, but in its characteristic feature finds crude prototypes in apparatus which employed the kinetic energy of jets of steam.

Fig. 1.—Hero’s Apparatus, 130 B.C.

2. One of these, indeed, is mentioned amongst the earliest notices we have of any heat engine. In the Pneumatica of Hero of Alexandria (c. 130 B.C.) there is described the aeolipile, which is a Hero, 130
B.C. primitive steam reaction turbine, consisting of a spherical vessel pivoted on a central axis and supplied with steam through one of the pivots. The steam escapes by bent pipes facing tangentially in opposite directions, at opposite ends of a diameter perpendicular to the axis. The globe revolves by reaction from the escaping steam just as a Barker’s mill is driven by escaping water. Another apparatus described by Hero (fig. 1)^[1] is interesting as the prototype of a class of engines which long afterwards became practically important. A hollow altar containing air is heated by a fire kindled on it; the air in expanding drives some of the water contained in a spherical vessel beneath the altar into a bucket, which descends and opens the temple doors above by pulling round a pair of vertical posts to which the doors are fixed. When the fire is extinguished the air cools, the water leaves the bucket, and the doors close. In another device a jet of water driven out by expanding air is turned to account as a fountain.

3. From the time of Hero to the 17th century there is no progress to record, though here and there we find evidence that appliances like those described by Hero were used for trivial purposes, such as organ-blowing and the Della Porta, 1601 turning of spits. The next distinct step was the publication in 1601 of a treatise on pneumatics by Giovanni Battista della Porta, in which he shows an apparatus similar to Herb’s fountain, but with steam instead of air as the displacing fluid. Steam generated in a separate vessel passes into a closed chamber containing water, from which a pipe (open under the water) leads out. He also points out that the condensation of steam in the closed chamber may be used to produce a vacuum and suck up water from a lower level. In fact, his suggestions anticipate very fully the engine which a century later became in the hands of Savery the earliest commercially successful steam engine. In 1615 Solomon de Caus gives a plan of forcing up water by a steam fountain which differs from Della Porta’s only in having one vessel serve both as boiler and as displacement-chamber, the hot water being itself raised.

4. Another line of invention was taken by Giovanni Branca (1629), who designed an engine shaped like a water-wheel, to be driven by the impact of a jet of steam on its vanes, and in its turn to drive other mechanism for various useful purposes. But Branca’s suggestion was for the time unproductive, and we find the course of invention reverting to the line followed by Della Porta and De Caus.

5. The next contributor is one whose place is not easily assigned. To Edward Somerset, second marquis of Worcester, appears to be due the credit of proposing, if not making, the first useful steam engine. Its object Marquis of Worcester, 1663. was to raise water, and it worked probably like Della Porta’s model, but with a pair of displacement-chambers, from each of which alternately water was forced by steam from an independent boiler, or perhaps by applying heat to the chamber itself, while the other vessel was allowed to refill. Lord Worcester’s description of the engine in art. 68 of his Century of Inventions (1663) is obscure, and no drawings are extant. It is, therefore, difficult to say whether there were any distinctly novel features except the double action; in particular, it is not clear whether the suction of a vacuum was used to raise water as well as the direct pressure of steam.

6. The steam engine first became commercially successful in the hands of Thomas Savery,^[2] who, in 1698, obtained a patent for a water-raising engine, shown in fig. 2. Steam is admitted to one of the oval vessels A, displacing Savery,
1698. water, which it drives up through the check-valve B. When the vessel A is emptied of water the supply of steam is stopped, and the steam already there is condensed by allowing a jet of cold water from a cistern above to stream over the outer surface of the vessel. This produces a vacuum and causes water to be sucked up through the pipe C and the valve D. Meanwhile steam has been displacing water
Fig. 2.—Savery’s Pumping Engine, 1698.

from the other vessel, and is ready to be condensed there. The valves B and D open only upwards. The supplementary boiler and furnace E are for feeding water to the main boiler; E is filled while cold and a fire is lighted under it; it then acts like the vessel of De Gaus in forcing a supply of feed-water into the main boiler F. The gauge cocks G, G are an interesting feature in detail. Another form of Savery’s engine had only one displacement-chamber and worked intermittently. In the use of artificial means to condense the steam, and in the application of the vacuum so formed to raise water by suction from a level lower than that of the engine, Savery’s engine was probably an improvement on Worcester’s; in any case it found what Worcester’s engine had failed to find—considerable employment in pumping mines and in raising water to supply houses and towns, and even to drive water-wheels. A serious difficulty which prevented its general use in mines was the fact that the height through which it would lift water was limited by the pressure the boiler and vessels could bear. Pressures as high as 8 or 10 atmospheres were employed—and that, too, without a safety-valve—but Savery found it no easy matter to deal with high-pressure steam; he complains that it melted his common solder, and forced him, as Desaguliers tells us, “to be at the pains and charge to have all his joints soldered with spelter.” Apart from this drawback, the waste of fuel was enormous, from the condensation of steam which took place on the surface of the water and on the sides of the displacement-chamber at each stroke; the consumption of coal was, in proportion to the work done, some twenty times greater than in a good modern steam engine. In a tract called The Miner’s Friend Savery alludes thus to the alternate heating and cooling of the water-vessel: “On the outside of the vessel you may see how the water goes out as well as if the vessel were transparent, for so far as the steam continues within the vessel so far is the vessel dry without and so very hot as scarce to endure the least touch of the hand. But as far as the water is, the said vessel will be cold and wet where any water has fallen on it; which cold and moisture vanishes as fast as the steam in its descent takes the place of the water.” Before Savery’s engine was entirely displaced by its successor, Newcomen’s, it was improved by J. T. Desaguliers, who applied to it the safety valve (invented by Papin), and substituted condensation by a jet of cold water within the vessel for the surface condensation used by Savery. To Savery is ascribed the first use of the term “horse power” as a measure of the performance of an engine.

7. So early as 1678 the use of a piston and cylinder (long before known as applied to pumps) in a heat-engine had been suggested by Jean de Hautefeuille, who proposed and to use the explosion of gun-powder either to raise a piston or to force up water, or to produce, by the subsequent cooling of the gases, a partial vacuum into Cylinder
and Piston Engine. which water might be sucked up. Two years later Christian Huygens described an engine in which the explosion of gunpowder in a cylinder expelled part of the gaseous contents, after which the cooling of the remainder caused a piston to descend under atmospheric pressure, and the piston in descending did work by raising a weight.

8. In 1690 Denis Papin, who ten years before had invented the safety-valve as an adjunct to his “digester,” suggested that the condensation of steam should be employed to make a vacuum under a piston previously raised by the expansion of the steam. Papin’s was the earliest cylinder and piston steam engine, and his plan of using steam Papin. was that which afterwards took practical shape in the atmospheric engine of Newcomen. But his scheme was made unworkable by the fact that he proposed to use but one vessel as both boiler and cylinder. A small quantity of water was placed at the bottom of a cylinder and heat was applied. When the piston had risen the fire was removed, the steam was allowed to cool, and the piston did work in its down-stroke under the pressure of the atmosphere. After hearing of Savery’s engine in 1705 Papin turned his attention to improving it, and devised a modified form, shown in fig. 3, in which the displacement-chamber A was a cylinder, with a floating diaphragm or piston on the top of the water to keep the water and steam from direct contact with one another. The water was delivered into a closed air-vessel B, from which it issued in a continuous stream, against the vanes of a water-wheel. After the steam had done its work in the displacement-chamber it was allowed to escape by the stop-cock C instead of being condensed. Papin's engine was, in fact, a non-condensing single-acting steam pump, with steam cylinder and pump cylinder in one. A curious feature of it was the heater D, a hot mass of metal placed in the diaphragm for the purpose of keeping the steam dry. Among the many inventions of Papin was a boiler with an internal fire-box—the earliest example of a construction that is now almost universal.^[3]

Fig. 3.—Papin, 1705.

9. While Papin was thus going back from his first notion of a piston engine to Savery’s cruder type, a new inventor had appeared who made the piston engine a practical success by separating the boiler from the cylinder and by using (as Savery had done) artificial means to condense the steam. This was Thomas Newcomen, Newcomen’s Atmospheric Engine, 1705.
Fig. 4.—Newcomen’s Atmospheric Engine, 1705. who in 1705, with his assistant, John Cawley, gave the steam engine the form shown in fig. 4. Steam admitted from the boiler to the cylinder allowed the piston to be raised by a heavy counterpoise on the other side of the beam. Then the steam valve was shut and a jet of cold water entered the cylinder and condensed the steam. The piston was consequently forced down by the pressure of the atmosphere and did work on the pump. The next entry of steam expelled the condensed water from the cylinder through an escape valve. The piston was kept tight by a layer of water on its upper surface. Condensation was at first effected by cooling the outside of the cylinder, but the accidental leakage of the packing water past the piston showed the advantage of condensing by a jet of injection water, and this plan took the place of surface condensation. The engine used steam whose pressure was little if at all greater than that of the atmosphere; sometimes, indeed, it was worked with the manhole lid off the boiler.

10. About 1711 Newcomen’s engine began to be introduced for pumping mines. It is doubtful whether the action was originally automatic, or depended on the periodical turning of taps by an attendant. The common story is that in 1713 a boy named Humphrey Potter, whose duty it was to open and shut the valves of an engine Self-acting Valve-gear. he attended, made the engine self-acting by causing the beam itself to open and close the valves by suitable cords and catches. This device was simplified in 1718 by Henry Beighton, who suspended from the beam a rod called the plug-tree, which worked the valves by means of tappets. By 1725 the engine was in common use in collieries, and it held its place without material change for about three-quarters of a century in all. Near the close of its career the atmospheric engine was much improved in its mechanical details by John Smeaton, who built many large engines of this type about the year 1770, just after the great step which was to make Newcomen’s engine obsolete had been taken by James Watt.

Compared with Savery’s engine, Newcomen’s had (as a pumping engine) the great advantage that the intensity of pressure in the pumps was not in any way limited by the pressure of the steam. It shared with Savery’s, in a scarcely less degree, the defect already pointed out, that steam was wasted by the alternate heating and cooling of the vessel into which it was led. Though obviously capable of more extended uses, it was in fact almost exclusively employed to raise water—in some instances for the purpose of turning water-wheels to drive other machinery. Even contemporary writers complain of its vast “consumption of fuel,” which appears to have been scarcely smaller than that of the engine of Savery.

11. In 1763 James Watt, an instrument maker in Glasgow, while engaged by the university in repairing a model of Newcomen’s engine, was struck with the waste of steam to which the alternate chilling and heating of the cylinder gave rise. He saw that the remedy, in his own words, would lie in keeping the cylinder as hot as the steam Watt,
1763. that entered it. With this view he added to the engine a new organ—an empty vessel separate from the cylinder, into which the steam should be allowed to escape from the cylinder, to be condensed there by the application of cold water either outside or as a jet. To preserve the vacuum in his condenser he added
Fig. 5.—Watt’s Experimental Apparatus. a pump called the air-pump, whose function was to pump from it the condensed steam and water of condensation, as well as the air which would otherwise accumulate by leakage or by being brought in with the steam or with the injection water. Then, as the cylinder was no longer used as a condenser, he was able to keep it hot by clothing it with non-conducting bodies, and in particular by the use of a steam jacket, or layer of hot steam between the cylinder and an external casing. Further, and still with the same object, he covered in the top of the cylinder, taking the piston-rod out through a steam-tight stuffing-box, and allowed steam instead of air to press upon the piston’s upper surface. The idea of using a separate condenser had no sooner occurred to Watt than he put it to the test by constructing the apparatus shown in fig. 5. There A is the cylinder, B a surface condenser, and C the air-pump. The cylinder was filled with steam above the piston, and a vacuum was formed in the surface condenser B. On opening the stop-cock D the steam rushed over from the cylinder and was condensed, while the piston rose and lifted a weight. After several trials Watt patented his improvements in 1769; they are described in his specification in the following words, which, apart from their immense historical interest, deserve careful study as a statement of principles which to this day guide the scientific development of the steam engine:—

“My method of lessening the consumption of steam, and consequently fuel, in fire-engines, consists of the following principles:—

“First, That vessel in which the powers of steam are to be employed to work the engine, which is called the cylinder in common fire-engines, and which I call the steam-vessel, must, during the whole time the engine is at work, be kept as hot as the steam that enters it; first by enclosing it in a case of wood, or any other materials that transmit heat slowly; secondly, by surrounding it with steam or other heated bodies; and, thirdly, by suffering neither water nor any other substance colder than the steam to enter or touch it during that time.

“Secondly, In engines that are to be worked wholly or partially by condensation of steam, the steam is to be condensed in vessels distinct from the steam-vessels or cylinders, although occasionally communicating with them; these vessels I call condensers; and, whilst the engines are working, these condensers ought at least to be kept as cold as the air in the neighbourhood of the engines, by application of water or other cold bodies.

“Thirdly, Whatever air or other elastic vapour is not condensed by the cold of the condenser, and may impede the working of the engine, is to be drawn out of the steam-vessels or condensers by means of pumps, wrought by the engines themselves, or otherwise.

“Fourthly, I intend in many cases to employ the expansive force of steam to press on the pistons, or whatever may be used instead of them, in the same manner in which the pressure of the atmosphere is now employed in common fire-engines. In cases where cold water cannot be had in plenty, the engines may be wrought by this force of steam only, by discharging the steam into the air after it has done its office. . . .

“Sixthly, I intend in some cases to apply a degree of cold not capable of reducing the steam to water, but of contracting it considerably, so that the engines shall be worked by the alternate expansion and contraction of the steam.

“Lastly, Instead of using water to render the pistons and other parts of the engine air and steam tight, I employ oils, wax, resinous bodies, fat of animals, quicksilver and other metals in their fluid state.”

The fifth claim was for a rotary engine, and need not be quoted here.

The “common fire engine” alluded to was the steam engine, or, as it was more generally called, the “atmospheric” engine of Newcomen. Enormously important as Watt’s first patent was, it resulted for a time in the production of nothing more than a greatly improved engine of the Newcomen type, much less wasteful of fuel, able to make faster strokes, but still only suitable for pumping, still single-acting, with steam admitted during the whole stroke, the piston, as before, pulling the beam by a chain working on a circular arc. The condenser was generally worked by injection, but Watt has left a model of a surface condenser made up of small tubes, in every essential respect like the condensers now used in marine engines.^[4]

12. Fig. 6 is an example of the Watt pumping engine of this period. It should be noticed that, although the top of the cylinder is closed and steam has access to the upper side of the piston, this is done only to keep the cylinder and piston warm. The engine is still single-acting; the steam in the upper side merely plays the part which was played in Newcomen’s engine by the atmosphere; and it is Watt’s Pumping Engine, 1769. the lower end of the cylinder alone that is ever put in communication with the condenser. There are three valves: the “steam” valve 𝑎, the “equilibrium” valve 𝑏, and the “exhaust” valve 𝑐. At the beginning of the down-stroke 𝑐 is opened to produce a vacuum below the piston and 𝑎 is opened to admit steam above it. At the end of the down-stroke 𝑎 and 𝑐 are shut and 𝑏 is opened. This puts the two sides in equilibrium and allows the piston to be pulled up by the pump-rod P, which is heavy enough to serve as a counterpoise. C is the condenser, and A the air-pump, which discharges into the hot well H, whence the supply of the feed-pump F is drawn.

13. In a second patent (1781) Watt describes the “sun-and-planet” wheels and other methods of making the engine give continuous revolving motion to a shaft provided with a flywheel. He had invented the crank and connecting-rod for this purpose, but it had meanwhile been patented by one Pickard, and Watt, rather than make terms with Pickard, whom he regarded as a plagiarist of Rotative Engine. his own ideas, made use of his sun-and-planet motion until the patent on the crank expired. The reciprocating motion of earlier forms had served only for pumping; by this invention Watt opened up for the steam engine a thousand other channels of usefulness. The engine was still single-acting; the connecting-rod was attached to the far end of the beam, and that carried a counterpoise which served to raise the piston when steam was admitted below it.

Fig. 6.—Watt’s Single- Acting Engine, 1769.

14. In 1782 Watt patented two further improvements of the first importance, both of which he had invented some years before. One was the use of double action, that is to say, the application of steam and vacuum to each side of the piston alternately. The other (invented as early as 1769) was the use of steam expansively, Other Inventions
of Watt. in other words the plan (now used in all engines that aim at economy of fuel) of stopping the admission of steam
Fig. 7.—Watt’s Double-Acting
Engine, 1782. when the piston had made only a part of its stroke, and allowing the rest of the stroke to be performed by the expansion of the steam already in the cylinder. To let the piston push as well as pull the end of the beam Watt devised his so-called parallel motion, an arrangement of links connecting the piston-rod head with the beam in such a way as to guide the rod to move in a very nearly straight line. He further added the throttle valve, for regulating the rate of admission of steam, and the centrifugal governor, a double conical pendulum, which controlled the speed by acting on the throttle-valve. The stage of development reached at this time is illustrated by the engine of fig. 7 (from Stuart’s History of the Steam Engine), which shows the parallel motion 𝑝𝑝, the governor 𝑔, the throttle-valve 𝑡, and a pair of steam and exhaust valves at each end of the cylinder. Among other inventions of Watt were the “indicator,” by which diagrams showing the relation of the steam pressure in the cylinder to the movement of the piston are automatically drawn; a steam tilt-hammer; and also a steam locomotive for ordinary roads—but this invention was not prosecuted.

In partnership with Matthew Boulton, Watt carried on in Birmingham the manufacture and sale of his engines with the utmost success, and held the field against all rivals in spite of severe assaults on the validity of his patents. Notwithstanding his accurate knowledge of the advantage to be gained by using steam expansively, he continued to employ only low pressures—seldom more than 7 ℔ per sq. in. over that of the atmosphere. His boilers were fed, as Newcomen’s had been, through an open pipe which rose high enough to let the column of water in it balance the pressure of the steam. He gave a definite numerical significance to the term “horse-power” (q.v.) as a mode of rating engines, defining it as the rate at which work is done when 33,000 ℔ are raised one foot in one minute.

15. In the fourth claim in Watt’s first patent the second sentence describes a non-condensing engine, which would have required steam of a higher pressure. This, however, was a line of invention which Watt did not follow up, perhaps because so early as 1725 a non-condensing engine had been described by Jacob Leupold Non-condensing Engine. in his Theatrum machinarum. Leupold’s proposed engine
Fig. 8.—Leupold’s Non-Condensing Engine, 1725. is shown in fig. 8, which makes its action sufficiently clear. Watt’s aversion to high-pressure steam was strong, and its influence on steam engine practice long survived the expiry of his patents. So much indeed was this the case that the terms “high-pressure” and “non-condensing” were for many years synonymous in contradistinction to the “low-pressure” or condensing engines of Watt. This nomenclature no longer holds; in modern practice many condensing engines use as high pressures as non-condensing engines, and by doing so are able to take advantage of Watt’s great invention of expansive working to a degree which was impossible in his own practice.

16. The introduction of the non-condensing and, at that time, relatively high-pressure engine was effected in England by Richard Trevithick and in America by Oliver Evans about 1800. Both Evans and Trevithick applied their engines to propel carriages on roads, and both used for boiler a cylindrical vessel with a cylindrical High-pressure Steam. flue inside—the construction now known as the Cornish boiler. In partnership with William Bull, Trevithick had previously made direct acting pumping-engines, with an inverted cylinder set over and in line with the pump-rod, thus dispensing with the beam that had been a feature in all earlier forms. But in these “Bull” engines, as they were called, a condenser was used, or, rather, the steam was condensed by a jet of cold water in the exhaust-pipe, and Boulton and Watt successfully opposed them as infringing Watt’s patents. To Trevithick belongs the distinguished honour of being the first to use a steam carriage on a railway; in 1804 he built a locomotive in the modern sense, to run on what had formerly been a horse-tramway, in Wales, and it is noteworthy that the exhaust steam was discharged into the funnel to force the furnace draught, a device which, twenty-five years later, in the hands of George Stephenson, went far to make the locomotive what it is to-day. In this connexion it may be added that as early as 1769 a steam carriage for roads had been built in France by Nicolas Joseph Cugnot, who used a pair of single-acting high-pressure cylinders to turn a driving axle step by step by means of pawls and ratchet-wheels. To the initiative of Evans may be ascribed the early general use of high-pressure steam in the United States, a feature which for many years distinguished American from English practice.

17. Amongst the contemporaries of Watt one name deserves special mention. In 1781 Jonathan Carter Hornblower constructed and patented what would now be called a compound engine, with two cylinders of different sizes. Steam was first admitted into the smaller cylinder, and then passed over into the larger, doing work Compound Engine. against a piston in each. In Hornblower’s engine the two cylinders were placed side by side, and both pistons worked on the same end of a beam overhead. This Was an instance of the use of steam expansively, and as such was earlier than the patent, though not earlier than the invention, of expansive working by Watt. Hornblower was crushed by the Birmingham firm for infringing their patent in the use of a separate condenser and air-pump. The compound engine was revived in 1804 by Arthur Woolf, with whose name it is often associated. Using steam of fairly high pressure, and cutting off the supply before the end of the stroke in the small cylinder, Woolf expanded the steam to several times its original volume. Mechanically the double-cylinder compound engine has this advantage over an engine in which the same amount of expansion is performed in a single cylinder, that the sum of the forces exerted by the two pistons in the compound engine Varies less throughout the action than the force exerted by the piston of the single-cylinder engine. This advantage may have been clear to Hornblower and Woolf and to other early users of compound expansion. But another and probably a more important merit of the system lies in a fact of which neither they nor for many years their followers in the use of compound engines were aware—the fact that by dividing the whole range of expansion into two parts the cylinders in which these are separately performed are subject to a reduced range of fluctuation in their temperature. This, as will be seen later, limits to a great extent a source of waste which is present in all steam engines, the waste which results from the heating and cooling of the metal by its alternate contact with hot and cooler steam. The system of compound expansion is now used in nearly all large engines that pretend to economy. Its introduction forms the most outstanding improvement which steam engines of the piston and cylinder type have undergone since the time of Watt; and we are able to recognize it as a very important step in the direction set forth in his “first principle” that the cylinder should be kept as hot as the steam that enters it.

18. Woolf introduced the compound engine somewhat widely about 1814 as a pumping engine in the mines of Cornwall. But here it met a strong competitor in the high-pressure single-cylinder engine of Trevithick, which had the advantage of greater simplicity in construction. Woolf’s engine fell into comparative disuse, and the Cornish Engine. single-cylinder type took a form which, under the name of the Cornish pumping engine, was for many years famous for its great economy of fuel. In this engine the cylinder was set under one end of a beam, from the other end of which hung a heavy rod which operated a pump at the foot of the shaft. Steam was admitted above the piston for a short portion of the stroke, thereby raising the pump-rod, and was allowed to expand for the remainder. Then an equilibrium valve, connecting the space above and below the piston, as in fig. 6, was opened, and the pump-rod descended, doing work in the pump and raising the engine piston. The large mass which had to be started and stopped at each stroke served by its inertia to counterbalance the unequal pressure of the steam, for the ascending rods stored up energy of motion in the early part of the stroke, when the steam pressure was greatest, and gave out energy in the later part, when expansion had greatly lowered the pressure. The frequency of the stroke was controlled by a device called a cataract, consisting of a small plunger pump, in which the plunger, raised at each stroke by the engine, was allowed to descend more or less slowly by the escape of fluid below it through an adjustable orifice, and in its descent liberated catches which held the steam and exhaust valves from opening. A similar device controlled the equilibrium valve, and could be set to give a pause at the end of the piston’s down-stroke, so that the pump-cylinder might have time to become completely filled. The Cornish engine is interesting as the earliest form which achieved an efficiency comparable with that of good modern engines. For many years monthly reports were published of the “duty” of these engines, the “duty” being the number of foot-pounds of work done per bushel or (in some cases) per cwt. of coal. The average duty of engines in the Cornwall district rose from about 18 millions of foot-pounds per cwt. of coal in 1813 to 68 millions in 1844; after which less effort seems to have been made to maintain a high efficiency (Proc. Inst. C.E., 1863, vol. 23). In individual cases much higher results were reported, as in the Fowey Consols engine, which in 1835 was stated to have a duty of 125 millions. This (to use a more modern mode of reckoning) is equivalent to the consumption of only a little more than 1 3/4 ℔ of coal per horse-power per hour—a result surpassed by very few engines in even the best recent practice. It is difficult to credit figures which, even in exceptional instances, place the Cornish engine of that period on a level with the most efficient modern engines—in which compound expansion and higher pressure combine to make a much more perfect thermodynamic machine; and apart from this there is room to question the accuracy of the Cornish reports. They played, however, a useful part in the process of steam engine development by directing attention to the question of efficiency, and by demonstrating the advantage to be gained by high pressure and expansive working, at a time when the theory of the steam engine had not yet taken shape.

19. The final revival of the compound engine did not occur until about the middle of the 19th century, and then several agencies combined to effect it. In 1845 M‘Naught introduced a plan of improving beam engines of the original Watt type, by adding a high-pressure cylinder whose piston acted on the beam between the centre Compound Engine. and the flywheel end. Steam of higher pressure than had formerly been used, after doing work in the new cylinder, passed into the old or low-pressure cylinder, where it was further expanded. Many engines whose power was proving insufficient for the extended machinery they had to drive were “M‘Naughted” in this way, and after conversion were found not only to yield more power but to show a marked economy of fuel. The compound form was selected by William Pole for the pumping engines of Lambeth and other waterworks about 1850; in 1854 John Elder began to use it in marine engines; in 1857 E. A. Cowper added a steam-jacketed intermediate reservoir for steam between the high and low pressure Cylinders, which made it unnecessary for the low-pressure piston to be just beginning when the other piston was just ending its stroke. As facilities increased for the use of high-pressure steam, compound expansion came into more, general use, its advantage becoming more conspicuous with every increase in boiler pressure—until now there are few large land engines and scarcely any marine engines that do not employ it. In marine practice, where economy of fuel is a much more important factor in determining the design than it is on land, the principle of compound expansion has been greatly extended by the introduction of triple and even quadruple expansion engines, in which the steam is made to expand successively in three or in four cylinders. In locomotive engines, where other considerations are of more moment than the saving of coal, compound expansion has found some application, but its use there is comparatively rare.

20. The adaptation of the steam engine to railways, begun by Trevithick, became a success in the hands of George Stephenson, whose engine, the “Rocket,” when tried along with others, in 1829, not only distanced its competitors but settled once and for all the question whether horse traction or steam traction was to be used Application to Locomotives. on railways. The principal features of the “Rocket” were an improved steam-blast for urging "the combustion of coal and a boiler (suggested by Booth) in which a large heating surface was given by the use of many small tubes through which the hot gases passed. Further, the cylinders, instead of being vertical as in earlier locomotives, were set in at a slope, which was afterwards altered to a position more nearly horizontal. To these features there was added later the “link motion,” a contrivance which enabled the engine to be easily reversed and the amount of expansion to be readily varied. In the hands of George Stephenson and his son Robert the locomotive took a form which has been in all essentials maintained by the far heavier locomotives of to-day.

21. The first practical steamboat was the tug “Charlotte Dundas,” built by William Symington, and tried in the Forth and Clyde Canal in 1802. A Watt double-acting condensing engine, placed horizontally, acted directly a connecting-rod on the crank of a shaft at the stern, which carried a revolving paddle-wheel. The trial Application to Steamboats. was successful, but steam towing was abandoned for fear of injuring the banks of the canal. Ten years later Henry Bell built the “Comet,” with side paddle-wheels, which ran as a passenger steamer on the Clyde; but an earlier inventor to follow up Symington’s success was the American, Robert Fulton, who, after unsuccessful experiments on the Seine, fitted a steamer on the Hudson in 1807 with engines made to his designs by Boulton and Watt, and brought steam navigation for the first time to commercial success.

22. With improvements in the details of design and construction it gradually became practicable to use higher steam pressures and higher piston speeds, and consequently to obtain not only greater efficiency, but also a greater amount of power from engines of given bulk. In 1872 Sir F. J. Bramwell, describing the typical Rise in Steam Pressure and in Piston Speed. marine practice of that time, gave a list of engines, all compound, in which the boiler pressure ranged from 45 to 60 ℔, the mean piston speed was 350 ft. per minute, and the consumption of coal 2 to 2 1/2 ℔ per hour per indicated horse-power. In 1881 F. C. Marshall gave a similar list, in which the boiler pressure was 77 ℔, the speed 460 ft. per minute, and the consumption a trifle under 2 ℔. These were compound engines with expansion in two stages. The triple expansion engine, introduced by Dr A. C. Kirk in 1874, did not come into general use until after 1881. It became the normal type of marine engine, with pressures ranging, as a rule, from 150 to 200 ℔, piston speeds generally of 500 or 600 ft. per minute, but sometimes as high as 900 or 1000, and coal consumption of about 1 1/2 ℔ per hour per indicated horse-power. In some Triple and Quadruple Expansion. instances quadruple expansion has been preferred, with somewhat higher pressures, but it can scarcely be said to be established that the advantage of adding a fourth stage clearly compensates for the extra complication. Some particulars of the dimensions reached in modern practice will be given later. Several of the vessels engaged in the Transatlantic passenger service, and also a few armoured cruisers, have engines in which the twin sets together have an indicated horse-power exceeding 30,000. But even these figures are eclipsed in ships which are driven by turbine engines. The cruisers of the “Invincible” class have turbine engines of 41,000 horse-power, and the turbines of the great Cunarders “Lusitania” and “Mauretania” (1907) develop about 70,000 h.p. in propelling these ships at a speed of 25 knots. It may be questioned whether such gigantic concentrations of power for the propulsion of a ship would have been practicable had it not been for the new possibilities which the introduction of the steam turbine has opened up.

23. The invention of the steam turbine has in fact revolutionized marine engine practice, so far as fast vessels are concerned, and has supplied a formidable rival to the reciprocating engine for use on land. The steam turbine has been brought to a degree of efficiency which places it, in respect of economy in steam Introduction of the Steam Turbine. than the best engines of the older type in cases where a large amount of power is to be generated. Its greater simplicity, compactness and freedom from vibration are merits which have already gone far to secure for it a preference, notwithstanding the short time that has passed since it became known as a practicable engine. The largest demands for power occur in fast passenger vessels, in war-ships and in stations from which electric energy is distributed for traction or other uses; in all these cases the steam turbine is now taking the leading place. It is to the inventive genius of the Hon. C. A. Parsons that we owe not only the main idea of the modern steam turbine, but also the working out of many novel mechanical details which have been essential to success, as well as the adaptation of the turbine to marine propulsion.

24. In the steam turbine, as in the water turbine (for which see Hydraulics), the force directly operative to do useful work is derived from the kinetic energy of the operative fluid, either by the impulse of a jet or jets sliding over movable blades, or by the reaction of orifices or guides from which the jets issue. The pressure, instead of being exerted on a piston, is employed in the first instance to set the fluid itself in motion. There is a conversion of pressure-energy into velocity-energy as a preliminary step towards obtaining the effective work of the machine. But in a steam turbine this implies velocities which are immensely greater than those with which water turbines have to deal, in consequence of the much smaller density of steam as the moving fluid. Attempts to design a steam turbine were made by numerous inventors, but fell short of practical success mainly because of the difficulty of arranging for a sufficiently high velocity in the working parts to utilize a reasonably large fraction of the kinetic energy of the steam, the principle involved being that for good efficiency the velocity of the blades should approximate to half the velocity of the jets which strike them. There is a further difficulty in getting the energy of the steam into a suitable kinetic form, namely, to get the stream of issuing particles to take a single direction, without undue dispersion, when steam is allowed to expand through an orifice from a chamber at high pressure into a space where the pressure is greatly less.

In 1889 Dr Gustaf de Laval introduced a form of steam turbine in which both of these difficulties were to a great extent overcome, partly by the special form of the nozzle used to produce the steam jet and partly by features of design which allowed an exceptionally high speed to be reached in the wheel carrying the vanes against which the steam impinged. This simple type of turbine, which will be described in a later section of this article, has met with considerable success, especially in comparatively small sizes, as an engine for driving electric generators. Its efficiency is fairly good, but it is not well adapted for work on a large scale, and it has not been applied to the propulsion of ships.

Parsons attacked the problem at an earlier date, in an entirely different way in the invention of his “compound” turbine. By dividing the whole expansion of the steam into a great number of successive and separate steps he limited the velocity acquired at each step to such an extent as to make it comparatively easy to extract the greater part of the kinetic energy, as work done upon the moving blades, without making the velocity of these blades inconveniently high. Moreover, in Parsons’s compound turbine the range of pressure through which the steam expands in each separate step is too small to give rise to any difficulty in the formation of the jets. The guide blades, which form the jets, are distributed round the whole circumference of the revolving wheel, and all the revolving blades are consequently in action at once. The steam streams from end to end through an annular space between a revolving drum and the casing which surrounds it. Parallel rings of fixed guide blades project inwards from the casing at suitable distances, and between these are rings of moving blades which project outwards from the drum and revolve with it. At each step in the expansion the steam streams through a ring of fixed guide blades, and the streams so formed impinge on the next ring of moving blades, and so on. The construction, which is of great simplicity, will be described later; it lends itself well to the generation of power on a large scale, especially in cases where a fairly high speed of rotation is wanted. The more powerful the turbine the less important do various inevitable sources of loss become; and hence, though the small turbines which were first built were less economical than reciprocating engines, the advantage is the other way where large powers are concerned.

25. Parsons introduced his compound steam turbine in 1884. For some years it was made in small sizes only, and the steam was discharged to the atmosphere without condensation. So long, however, as this was done the steam turbine was sacrificing one of its most important advantages, namely, its exceptional capacity for utilizing the energy of low-pressure steam down to the lowest vacuum obtainable in a condenser. In 1891 it was first fitted with a condenser, and it then began to be used in electric supply stations. Its efficiency at that date was found, in tests made by the present writer, to be comparable with that of good reciprocating compound engines, but the figures then obtained were much improved on later in turbines of larger size and modified design. The first application to marine propulsion was in the “Turbinia,” in 1897. The success of this little experimental vessel of 100 tons, which with its horse-power of 2100 made a record in speed for a ship of any size, was soon followed by the application of the turbine to various war-ships and other steamers. In war-ships the use of steam turbines has a special advantage in enabling the machinery to be kept at a low level, beneath the protective deck, in addition to the general advantages of reduced bulk, reduced vibration, reduced liability to break-down, and reduced consumption of coal and of oil which are common to vessels of all classes. The successful trials of the cruiser “Amethyst” in 1904 demonstrated these advantages so conclusively that all new war-ships for the British navy, from battleships to torpedo-boats are being fitted with steam turbines. It is also used in many cross-channel packets, as well as in the largest ocean-going passenger vessels. The turbine-driven steamers “Lusitania” and “Mauretania” (1907) are the most powerful and the fastest ocean-going vessels afloat. The rapid development of the marine steam turbine makes it probable that it will displace the reciprocating engine in all large and fast ships. For slow-going cargo-boats it is at a disadvantage, unless gearing is resorted to, on account of the difficulty of securing a sufficiently high peripheral velocity in the turbine drums without making the turbines unduly bulky, and the leakage losses (due to steam passing through the clearance spaces over the tips of the blades) unduly large. Experiments by Parsons (Trans. Inst. Nav. Arch., 1910) on a ship in which a slow-running propeller is driven through reducing-gear from a high-speed turbine, have given highly promising results.

Enough has been said to show that the invention of the steam turbine is the most important step in steam engineering since the time of Watt. It is the first solution of the problem of using steam efficiently in an engine without reciprocating parts. The object in most steam engines is to deliver power to revolving machinery, and much ingenuity has been expended in attempts to devise engines which will produce rotation directly, instead of by conversion of reciprocating motion. No rotary engine, however, was permanently successful until the steam turbine took a practical form.

26. In the early development of the steam engine inventors had little in the way of theory to guide them. Watt had the advantage, which he acknowledges, of a knowledge of Joseph Black’s doctrine of latent heat; but there was no philosophy of the relation of work to heat until long after the inventions of Watt were complete. The theory of the steam engine as a heat engine dates from 1824, when N. L. Sadi Carnot published his Réflexions sur Theory of Steam Engine. la puissance motrice du feu, and showed that heat does work only by being let down from a higher to a lower temperature. But Carnot had no idea that any of the heat disappears in the process, and it was not until the doctrine of the conservation of energy was established in 1843 by the experiments of J. P. Joule that the theory of heat engines began a vigorous growth. From 1849 onwards the science of thermodynamics was developed with extraordinary rapidity by R. J. M. Clausius, W. J. Macquorn Rankine and William Thomson (Lord Kelvin) and was applied, especially by Rankine, to practical problems in the use of steam. The publication in 1859 of Rankine’s Manual of the Steam Engine formed an epoch in the history of the subject by giving inventors a new basis, outside of mere empiricism, from which they could push on the development of the steam engine. Unfortunately, however, it was assumed that the cylinder and piston might be treated as behaving to the steam like non-conducting bodies—that the transfer of heat between the steam and the metal was negligibly small. Rankine’s calculations of steam consumption, work and thermodynamic efficiency involve this assumption, except in the case of steam-jacketed cylinders, where he estimates that the steam in its passage through the cylinder takes just enough heat from the jacket to prevent a small amount of condensation which would otherwise occur as the process of expansion goes on. If the transfer of heat from steam to metal could be overlooked, the steam which enters the cylinder would remain during admission as dry as it was before it entered, and the volume of steam consumed per stroke would correspond with the volume of the cylinder up to the point of cut-off. It is here that the actual behaviour of steam in the cylinder diverges most widely from the behaviour which the theory assumes. When steam enters the cylinder it finds the metal chilled by the previous exhaust, and a portion of it is at once condensed. This has the effect of increasing, often very largely, the volume of boiler steam required per stroke. As expansion goes on the water that was condensed during admission begins to be re-evaporated from the sides of the cylinder, and this action is often prolonged into the exhaust. It is now recognized that any theory which fails to take account of these exchanges of heat between the steam and its metal envelope fails also to yield even comparatively correct results in calculating the relative efficiency of various steam pressures or various ranges of expansion. But the exchanges of heat are so complex that there seems little prospect of submitting them to any comprehensive theoretical treatment, and information is rather to be sought from the scientific analysis of experiments with actual machines.

27. Formation of Steam under Constant Pressure.—In attempting a brief sketch of steam engine theory it is necessary to begin by giving some account of the properties of steam, so far as they are relevant. The properties of steam are most conveniently stated by referring in the first instance to what happens when steam is formed under constant pressure. This is substantially the process which occurs in the boiler of a steam engine when the engine is at work. To fix the ideas we may suppose that the vessel in which steam is to be formed is a long upright cylinder fitted with a piston which may be loaded so that it exerts a constant pressure on the fluid below. Let there be, to begin with, at the foot of the cylinder a quantity of water (which for convenience of numerical statement we shall take as 1 ℔), at any temperature 𝑡₀; and let the piston press on the surface of the water with a force of 𝑝 ℔ per square foot. Let heat now be applied to the bottom of the cylinder. As it enters the water it will produce the following effects in three stages:—

1. The temperature of the water rises until a certain temperature 𝑡 is reached, at which steam begins to be formed. The value of 𝑡 depends on the particular pressure 𝑝 which the piston exerts. Until the temperature 𝑡 is reached there is nothing but water below the piston.

2. Steam is formed, more heat being taken in. The piston (which is supposed to exert a constant pressure) rises. No further increase of temperature occurs during this stage, which continues until all the water is converted into steam. During this stage the steam which is formed is said to be saturated. The volume which the piston encloses at the end of this stage—the volume, namely, of 1 ℔ of saturated steam at pressure 𝑝 (and temperature 𝑡)—will be denoted by 𝑣 in cubic feet.

3. If after all the water is converted into steam more heat be allowed to enter, the volume will increase and the temperature will rise. The steam is then said to be superheated.

The difference between saturated and superheated steam may be expressed by saying that if water (at the temperature of the steam) be mixed with steam some of the water will be evaporated if the steam is superheated, but none if the steam is saturated. Any vapour in contact with its liquid and in thermal equilibrium is necessarily saturated. When saturated its properties differ considerably, as a rule, from those of a perfect gas, especially at high pressures, but when superheated they approach those of a perfect gas more and more closely the further the process of superheating is carried, that is to say, the more the temperature is raised above 𝑡, the temperature of saturation corresponding to the given pressure 𝑝.

28. Relation of Pressure and Temperature in Saturated Steam.—The temperature 𝑡 at which steam is formed depends on the value of 𝑝. Their relation was determined with great care by Regnault (Mem. Inst. France, vol. xxi.). The pressure of saturated steam rises with the temperature at a rate which increases rapidly in the upper regions of the scale. This will be apparent from the first and second columns of the following table. The first column gives the temperature on the Centigrade scale; the second gives the corresponding pressure in pounds per square inch.

29. Relation of Volume and Temperature.—The same table shows the volume 𝑣 in cubic feet occupied by 1 ℔ of saturated steam at each temperature. This is based on the investigations of H. L. Callendar who has shown (see Thermodynamics and Vaporization) that an equation of the form

𝑣＝Rτ/𝑝 + 𝑏 − 𝑐

is applicable to water vapour, whether saturated or superheated, within the limits of experimental error throughout the range of pressure that is important in engineering practice. In this equation τ is the absolute temperature, R and 𝑏 are constants and 𝑐 is a term varying inversely as a certain power of the temperature. By aid of this equation, in conjunction with the results of various experiments on the latent heat and other properties of steam, Callendar has shown that it is possible to frame expressions from which numerical values of all the important properties of steam may be derived throughout a range of saturation temperatures extending from 0° C. to 200° C. or so. The values so obtained are thermodynamically consistent with one another, and are in good agreement with the most authoritative experimental results. They are accordingly to be accepted in lieu of those given in earlier steam tables which depended on measurements by Regnault, and are now known to be in some particulars erroneous. R. Mollier has applied Callendar’s method with great completeness to the calculation of steam tables, and the figures given here are adapted from his results.^[5] In addition to the relation of temperature, pressure and volume, the table shows other properties of steam which will be explained as we proceed.

30. Supply of Heat in Formation of Steam under Constant Pressure.—We have next to consider the supply of heat in the imaginary experiment of § 27. During the first stage, until the temperature rises from its initial value 𝑡₀ to 𝑡, the temperature at which steam begins to form under the given pressure, heat is required only to warm the water. Since the specific heat of water is nearly constant, the amount of heat taken in during the first stage is approximately 𝑡—𝑡₀ thermal units, or J (𝑡—𝑡₀) foot-pounds, J being Joule’s equivalent, and this expression for it will generally serve with sufficient accuracy in practical calculations. More exactly, however, the heat taken in is somewhat greater than this at high temperatures, for Regnault’s experiments show that the specific heat of water increases slightly as the temperature rises. In stating the amount of heat required for this first stage, to must be taken as a known temperature; for convenience in numerical statement the temperature 0° C. is usually chosen as an arbitrary starting-point from which the reception of heat is to be reckoned. We shall employ the symbol ℎ to designate the heat required to raise 1 ℔ of water from 0° C. to the temperature 𝑡 at which steam begins to form. During the first stage, sensibly all the heat supplied goes to increase the stock of internal energy which the fluid possesses, the amount of external work which is done by the expansion of the fluid being negligible.

The heat taken in during the second stage is what is called the latent heat of steam, and is denoted by L. Of it a part is spent in doing external work, namely, 𝑝 multiplied by the excess of the volume of the steam 𝑣 over the volume of the water 𝑤, and the remainder is the difference of internal energy between 1 ℔ of steam at 𝑡 and 1 ℔ of water at 𝑡.

31. Total Heat of Steam.—Adding together the heat taken in during the first and second stages, we have a quantity designated by H which may be called the heat of formation of 1 ℔ of saturated steam:—

H＝ℎ+L.

The heat of formation of 1 ℔ of steam, when formed under constant pressure from water at any temperature to, is H−ℎ₀, where ℎ₀ corresponds to 𝑡₀.

It has been pointed out by Mollier that for the purpose of calculations in technical thermodynamics it is convenient to add to the heat of formation the quantity 𝑝𝑤/J, which represents the thermal equivalent of the work spent in introducing the water under the piston, against the constant pressure 𝑝, before the operation of heating imagined in § 27 begins, 𝑤 being the volume of the water. We thus obtain a quantity which in its numerical values differs only very slightly from H, namely

I＝H+𝑝𝑤/J.

We shall call this the total heat of saturated steam. Values of I are stated in the table. Since the volume of 1 ℔ of water is only 0·016 cub. ft. the term 𝑝𝑤/J is numerically insignificant except at the highest pressures. Similarly, in reckoning the total heat of water I_𝑤 we add 𝑝𝑤/J to ℎ, and this quantity is also given in the table. The latent heat L is to be found from the table by subtracting I_𝑤, the total heat of water, from the total heat of steam. We shall use the centigrade scale of temperature throughout this article, and accordingly the total heats are expressed in terms of a unit involving the centigrade degree, namely, the quantity of heat required to raise the temperature of unit mass of water through 1° C. at 15° C. With this unit of heat the mechanical equivalent J is 1400 foot-pounds when the unit of mass is the ℔, and is 427 kilogram-metres when the unit of mass is the kilogramme.

*Properties of Saturated Steam.*
Tempera- ture. Centigrade.	Pressure ℔ per sq. in.	Volume cub. ft. per ℔.	Total Heat.		Entropy.
Tempera- ture. Centigrade.	Pressure ℔ per sq. in.	Volume cub. ft. per ℔.	Of Water.	Of Steam.	Of Water.	Of Steam.
0	0·089	3283.	0	594·7	0	2·178
5	0·127	2354.	5·0	597·1	0·018	2·148
10	0·178	1708.	10·0	599·4	0·036	2·119
15	0·246	1253.	15·0	601·8	0·054	2·091
20	0·336	931.	20·0	604·1	0·071	2·064
25	0·455	699·5	25·0	606·5	0·088	2·039
30	0·610	530·7	30·0	608·8	0·104	2·015
35	0·809	406·8	35·0	611·1	0·121	1·991
40	1·062	314·8	40·1	613·5	0·137	1·969
45	1·381	245·8	45·1	615·8	0·153	1·947
50	1·78	193·7	50·1	618·0	0·169	1·927
55	2·27	153·9	55·1	620·3	0·184	1·907
60	2·88	123·3	60 1	622·6	0·199	1·888
65	3·61	99·5	65·2	624·8	0·214	1·870
70	4·51	80·9	70·2	627·0	0·229	1·852
75	5·58	66·24	75·3	629·2	0·244	1·835
80	6·86	54·60	80·3	631·3	0·258	1·819
85	8·38	45·29	85·3	633·5	0·272	1·803
90	10·16	37·79	90·4	635·6	0·286	1·788
95	12·26	31·71	95·5	637·6	0·300	1·773
100	14·70	26·75	100·5	639·7	0·314	1·759
105	17·52	22·69	105·6	641·7	0·327	1·745
110	20·79	19·34	110·7	643·6	0·340	1·732
115	24·55	16·56	115·8	645·5	0·354	1·719
120	28·83	14·25	120·9	647·4	0·367	1·706
125	33·72	12·30	126·0	649·2	0·379	1·694
130	39·26	10·67	131·1	651·0	0·392	1·682
135	45·51	9·29	136·2	652·8	0·405	1·671
140	52·56	8·12	141·3	654·5	0·417	1·660
145	60·42	7·13	146·4	656·1	0·430	1·649
150	69·24	6·274	151·6	657·8	0·442	1·638
155	79·04	5·542	156·7	659·3	0·454	1·628
160	89·93	4·910	161·9	660·8	0·466	1·618
165	101·98	4·363	167·1	662·3	0·478	1·608
170	115·27	3·891	172·2	663·7	0·489	1·599
175	129·9	3·478	177·4	665·0	0·501	1·589
180	145·9	3·116	182·6	666·3	0·512	1·580
185	163·4	2·800	187·9	667·6	0·524	1·571
190	182·6	2·523	193·1	668·8	0·535	1·563
195	203·4	2·279	198·3	670·0	0·546	1·554
200	226·0	2·063	203·6	671·1	0·557	1·546
205	250·5	1·874	208·9	672·2	0·568	1·538
210	277·2	1·703	214·1	673·2	0·579	1·530
215	306·8	1·546	219·4	674·1	0·590	1·522

32. Internal Energy.—Of the heat of steam the part 𝑝𝑣/J is spent in doing external work. The remainder has gone to increase the stock of internal energy which the substance possesses.

In dealing with the heat required to produce steam we adopted the state of water at 0°C. as an arbitrary starting-point from which to reckon the reception of heat. In the same way it is convenient to use this arbitrary starting-point in reckoning what may be called the internal energy of the substance, which is the excess of the heat taken in over the external work done by the substance during its reception of heat. Thus the internal energy E of 1 ℔ of saturated steam at pressure 𝑝 is equal to the total heat I, less that part of the total heat which is spent in doing external work, or

E＝I−𝑝𝑣/J.

The notion of internal energy is useful in calculating the heat taken in or rejected by steam during any stage of its expansion or compression in an engine. When a working substance passes from one condition to another its gain or loss of heat is determined by the equation

Heat taken in＝increase of internal energy+external work.

Any of the terms of this equation may be negative; the last term is negative when work is done, not by but upon the substance.

33. Wet Steam.—In calculations which relate to the action of steam in engines we have often to deal, not with dry saturated steam, but with wet steam, or steam which either carries in suspension, or is otherwise mixed with, a greater or less proportion of water. In any such mixture, assuming it to be in equilibrium, the steam and water have the same temperature, and the steam is saturated. The dryness of wet steam is measured by the proportion 𝑞 of dry steam in each pound of the mixed substance. When that is known it is easy to determine the other physical constants: thus—

Latent heat of 1 ℔ of wet steam	＝𝑞L;
Total heat of 1 ℔ of wet steam	＝I_𝑤+𝑞L;
Volume of 1 ℔ of wet steam	＝𝑞𝑣+(1−𝑞)_𝑤
	＝𝑞𝑣 very nearly,

unless the steam is so wet as to consist mainly of water.

34. Superheated Steam.—Steam is superheated when its temperature is raised, in any manner, above the temperature corresponding to saturation at the actual pressure. When considerably superheated, steam approximates in behaviour to a perfect gas.

The specific heat during superheating is nearly constant at low pressures, its value being approximately 0·48; at high pressures it is higher, especially when the amount of superheating is slight. Callendar’s equations enable it to be calculated for any assigned conditions of temperature and pressure. They also allow a direct determination to be made of the total heat of superheated steam of given temperature and pressure, and from this, by comparison with the total heat of saturated steam at the same pressure, the mean specific heat over any stated range of superheating, may be found. Calling I_𝑠, the total heat of steam in the saturated condition, when the temperature is 𝑡, κ the mean specific heat in superheating at constant pressure to a higher temperature 𝑡′ and I′ the total heat in the superheated state, we have

I′＝I_𝑠, +κ(𝑡′−𝑡).

The following are values of κ:—

Temperature of Superheat 𝑡′ in °C.	Temperature of Saturation 𝑡 in °C.
Temperature of Superheat 𝑡′ in °C.	80°	120°	160°	180°	200°
100°	0·49
150°	0·49	0·51
200°	0·49	0·51	0·54	0·57
250°	0·48	0·50	0·53	0·56	0·59
300°	0·48	0·50	0·52	0·54	0·57
350°	0·48	0·49	0·51	0·53	0·56
400°	0·48	0·49	0·51	0·52	0·55
450°	0·48	0·49	0·51	0·52	0·54

35. Isothermal Expansion of Steam.—The expansion of volume which occurs during the conversion of water into steam under constant pressure is isothermal. From what has been already said it is obvious that steam, or any other saturated vapour, can be expanded or compressed isothermally only when wet, and that evaporation (in the one case) or condensation (in the other) must accompany the process. Isothermal lines for a working substance which consists of a liquid and its vapour are straight lines of uniform pressure.

36. Adiabatic Expansion of Steam.—If steam initially dry be allowed to expand adiabatically (namely, without taking in or giving out any heat) it becomes wet. A part of the steam is condensed by the process of adiabatic expansion, at first in the form of minute particles suspended throughout the mass. The temperature and pressure fall; and, as that part of the substance which remains uncondensed is saturated, the relation of pressure to temperature throughout the expansion is that which holds for saturated steam. Before expansion let the initial dryness of the steam be 𝑞₁ and its absolute temperature τ. Then, if it expand adiabatically until its temperature falls to τ, its dryness after expansion may be shown to be

𝑞＝τ/L (𝑞₁L₁/τ₁ + log_ετ₁/τ).

L₁, and L are the latent heats (in thermal units) of 1 ℔ of steam before and after expansion respectively. When the steam is dry to begin with, 𝑞₁＝1.

This formula is easily applied to the construction of the adiabatic curve when the initial pressure and the pressure after expansion are given, the corresponding values τ and L being found from the table.

37. Ideal Action of Heat Engine.—According to the principles of thermodynamics (q.v.), the action of a heat engine depends on its receiving heat at a temperature higher than that at which it is capable of rejecting heat to surrounding objects. The working substance in the engine must necessarily pass from an upper temperature, at which it takes in heat, to a lower temperature, at which it rejects heat, the difference, between the heat taken in and the heat rejected being the thermal equivalent of the work done. It may readily be shown that when the conditions are such as to make this difference as great as possible—in other words, to make the efficiency reach its ideal limit—the ratio of the heat taken in to the heat rejected depends only on the temperature at which reception and rejection of heat occur. Calling τ₁ and τ₂ the absolute temperatures at which heat is taken in and rejected respectively, and Q₁ and Q₂ the quantities of heat taken in and rejected, the limit of efficiency is reached when Q₁/Q₂＝τ₁/τ₂. The efficiency then has the value

(Q₁−Q₂)/Q₁＝(τ₁ − τ₂)/τ₁

and W, the work done, is Q₁(τ₁ − τ₂)/τ₁.

In the ideal engine imagined by Carnot the action is of this simple character. The working substance is brought by adiabatic compression from the lower to the upper extreme of temperature. It then takes in heat, without changing in temperature. Next, it expands adiabatically until its temperature falls to the lower extreme and finally at that temperature it rejects enough heat to restore it to its initial state, thereby completing a cycle of operations.

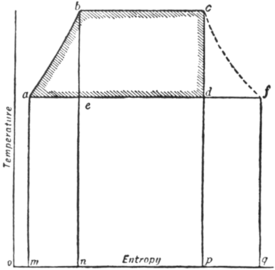
38. Carnot’s Cycle with Steam for Working Substance.—We are now in a position to study the action of a heat engine employing steam as the working substance. To simplify the first consideration as far as possible, let it be supposed that we have a long cylinder composed of non-conducting material except at the base, and fitted with a non-conducting piston; also a source of heat A at some temperature τ₁; a receiver of heat, or, as we may now call it, a condenser C, at a lower temperature τ₂; and a non-conducting cover B. Then We can perform as follows the ideal reversible cycle of operations first described by Carnot, which gives the highest possible efficiency attainable in any heat engine. To fix the ideas, suppose that there is 1 ℔ of water in the cylinder to begin with, at the temperature τ₁:—


	Fig. 9.—Carnot’s Cycle with water and steam for working substance.

1. Apply A, and allow the piston to rise. The water will take in heat and be converted into steam, expanding isothermally at constant pressure 𝑝₁. This part of the operation is shown by the line 𝑎𝑏 in fig. 9.

2. Remove A and apply B. Allow the expansion to continue adiabatically (𝑏𝑐), with falling pressure, until the temperature falls to τ₂. The pressure will then be 𝑝₂, namely, the pressure given in the table corresponding to τ₂.

3. Remove B, apply C, and compress. Steam is condensed by rejecting heat to C. The action is isothermal, and the pressure remains 𝑝₂. Let this be continued until a certain point 𝑑 is reached, after which adiabatic compression will complete the cycle.

4. Remove C and apply B. Continue the compression, which is now adiabatic. If the point 𝑑 has been rightly chosen, this will complete the cycle by restoring,the working fluid to the state of water at temperature τ₁.

The “indicator diagram” or diagram exhibiting the relation of pressure to volume for such a cycle is given in fig. 9. Since the process is reversible, and since heat is taken in only at τ₁ and rejected only at τ₂, the ideal conditions for perfect efficiency are satisfied, and accordingly the efficiency is (τ₁−τ₂)/τ₁. The heat taken in per ℔ of the fluid is L₁, and the work done is L₁(τ₁−τ₂)/τ₁, a result which may be used to check the calculation of the diagram.

39. Efficiency of a Perfect Steam Engine: Limits of Temperature.— If the action here described could be realized in practice, we should have a thermodynamically perfect steam engine using saturated steam. The fraction of the heat supplied to it which such an engine would convert into work would depend simply on the temperature, and therefore on the pressure, at which the steam was produced and condensed. The temperature of condensation is limited by the consideration that there must be an abundant supply of some substance to absorb the rejected heat; water is actually used for this purpose, so that τ₂ has for its lower limit the temperature of the available water-supply.

To the higher temperature τ₁ a practical limit is set by the mechanical difficulties, with regard to strength and to lubrication, which attend the use of high-pressure steam. In engines of ordinary construction the pressure is rarely so much as 250 ℔ per sq. in.

It must not be supposed that the efficiency (τ₁−τ₂)/τ₁ is actually attained, or is even attainable. Many causes conspire to prevent steam engines from being thermodynamically perfect, and some of the causes of imperfection cannot be removed.

Fig. 10.—Organs of a Steam Engine.

40. Engine with Separate Organs.—In the ideal engine represented in fig. 10 the functions of boiler, cylinder and condenser are combined in a single vessel; but, provided the working substance passes through the same cycle of operations, it is indifferent whether these are performed in several vessels or in one. To approach a little more closely the conditions that hold in practice, we may think of the engine as consisting of a boiler A (fig. 10) kept at τ₁, a non-conducting cylinder and piston B, a surface condenser C kept at τ₂, and a feed-pump D which restores the condensed water to the boiler. When the several organs of the engine are separated in this way we can still carry out the first three stages of the cyclic process described in § 38. The first stage of that cycle corresponds to the admission of steam from the boiler into the cylinder. Then the point known as the point of cut-off is reached, at which admission ceases, and the steam already in the cylinder is allowed to expand, exerting a diminishing pressure on the piston. This is the second stage, or the stage of expansion. The process of expansion may be carried on until the pressure falls to that of the condenser, in which case the expansion is said to be complete. At the end of the expansion release takes place, that is to say, communication is opened with the condenser. Then the return stroke begins, and a period termed the exhaust occurs, that is to say, steam passes out of the cylinder, into the condenser, where it is condensed at the pressure in the condenser, which is felt as a back pressure opposing the return of the piston. So far, all has been essentially reversible and identical with the corresponding parts of Carnot’s cycle.

But we cannot complete the cycle as Carnot’s cycle was completed. The existence of a separate condenser makes the fourth stage, that of adiabatic compression, impracticable, and the best we can do is to continue the exhaust until condensation is complete, and then return the condensed water to the boiler.

41. Rankine Cycle.—It follows that the ideal cycle of Carnot is not an appropriate standard with which to compare the action of a real steam engine. Instead of it we have, in the engine with separated organs, a cycle which is commonly called the Rankine cycle, which differs from the Carnot cycle only in this, that the stage of adiabatic compression, is wanting and its place is taken by a direct return of the condensed water to the boiler, a process which makes the water receive heat at various temperatures, ranging from the temperature of the condenser up to that of the boiler. The chief part of the heat which the working substance receives is still taken in at the upper limit of temperature, during the process of changing from water to steam. But a small part is taken in at lower temperatures, namely, in the heating of the feed water in its transfer to the boiler. Any heat so taken in has less availability for conversion into work than if it were taken in at the top of the range, and consequently the ideal efficiency of the cycle falls somewhat short of this ideal reached in the cycle of Carnot.

But the principle still applies that with respect to each portion of the heat that is taken in, the fraction convertible into work under ideally favourable conditions is measured by (τ−τ₂)/τ, where τ is the absolute temperature at which that portion of heat is received, and τ₂ is the temperature at which heat is rejected. Accordingly, we may investigate as follows the ideal performance of an engine following the Rankine cycle. Let δQ represent that portion of the whole heat which is taken in at any temperature τ. Then the greatest amount of work obtainable from that portion of heat is δQ(τ−τ₂)/τ, and the whole amount of work ideally obtainable in the complete process is found by calculating, ΣδQ(τ−τ₂)/τ where the summation includes all the heat that is taken in. In a steam engine using saturated steam the principal item in this sum is the latent heat L₁, which is taken in at constant temperature τ₁, during the change of state from water to steam. But there is, in addition, the heat taken in by the feed-water before it reaches the temperature at which steam is formed, and this may be represented as the sum of a series of elements σδτ taken in at varying temperatures τ, where σ is the specific heat of water. Thus if W represents the thermal equivalent of the work theoretically obtainable per ℔ of steam, under ideally favourable conditions,

W＝Σσδτ(τ−τ₂)/τ + L₁(τ₁−τ₂)/τ₁.

The experiments of Regnault show that σ, within the limits of temperature that obtain in boilers, is a nearly constant quantity, and no serious error will be introduced in this integration by treating it as a constant, with a value equal to the mean value, as determined by Regnault, between the limits of τ₁ and τ₂. On this basis

W＝σ(τ₁−τ₂)−στ₂ log_ετ₁/τ₂ + L₁(τ₁−τ₂)/τ₁.

It is usual to take σ as practically equal to 1, which makes

W＝(τ−τ₂)(1 + L₁/τ₁) − τ₂ log_ετ₁/τ₂.

This expresses the greatest amount of work which each pound of steam can yield when the temperature τ₁ at which it reaches the engine and the temperature τ₂ at which it leaves the engine are assigned. It consequently serves as a standard with which the actual performance may usefully be compared. The actual yield per ℔ of steam is always considerably less, chiefly because the ideal condition of adiabatic expansion from the higher to the lower extreme of temperature is never satisfied.

A more simple expression for the work theoretically obtainable per lb of steam when expanded adiabatically under the conditions of the Rankine cycle, is

I₁−I₂,

where I₁ is the total heat of the working substance in the initial state, before the adiabatic expansion, and I₂ is its total heat after that expansion. For it may readily be proved that, in an adiabatic process,

I₁−I₂＝1/J $\int _{p_{2}}^{p_{1}}$ 𝑣𝑑𝑝,

and this integral is the area of the indicator diagram when the substance is taken in at 𝑝₁, expanded to 𝑝₂ and discharged at 𝑝₂.

This expression applies whether the steam is initially superheated or not. I₂ will in general be the total heat of a wet mixture, and to calculate it we must know the condition as to wetness which results from the expansion. This is most easily found, especially when there has been initial superheat, by making use of the entropy-temperature diagram to be presently described, or by other graphic methods, for an account of which the reader should refer to the paper by Mollier already cited, or to J. A. Ewing’s The Steam Engine and other Heat Engines (3rd ed.).

42. Entropy.—The study of steam-engine problems is greatly assisted by introducing the idea of entropy and making use of diagrams in which the two co-ordinates are entropy and temperature. Entropy is a condition of the working substance defined by the statement that when any quantity of heat δQ is received by, or generated in, or rejected by the substance, when its absolute temperature is τ, the substance gains or loses entropy by the amount δQ/τ. Thus ΣδQ/τ measures the whole change of entropy in a process which involves the taking in or rejection of heat at more than one temperature. We shall denote entropy by φ, and consider it as reckoned per unit of mass of the substance. Since by definition of entropy δφ＝δQ/τ, τδφ＝δQ, and hence if a curve be drawn with τ and φ for ordinates to exhibit the action of a working substance, the area under the curve, or ∫τ𝑑φ, being equal to ΣδQ, measures the heat which the substance has received or rejected during the operation which the curve represents.

In a reversible cycle of operations Carnot’s principle shows that ΣδQ/τ＝0, and it is obvious in such a case that the entropy returns at the end of the cycle to its primitive value. The same result may be extended to a cycle which includes any non-reversible step, by taking account of the heat generated within the substance by such a step, as if it were heat communicated from outside, in the reckoning of entropy. Thus, for example, if at one stage in the cycle the substance passes through a throttle-valve, which lowers its pressure without letting it do work, the action is equivalent in effect to an adiabatic expansion, together with the communication to the substance, as heat, of the work which is lost in consequence of the irreversible expansion through the throttle-valve taking the place of adiabatic expansion against a piston. If this heat be included in the reckoning ΣδQ/τ＝0 for the complete cycle.

The entropy-temperature diagram for any complete cyclic process is a closed curve, and the area it encloses, being the excess of the heat received over the heat rejected, measures the work done. The entropy-temperature diagram shares this useful characteristic with the pressure-volume diagram, and in addition it shows directly the heat received and the heat rejected by the areas under the forward and backward limbs of the curve. To draw the entropy-temperature diagram for the ideal steam engine (namely, the engine following the Rankine cycle), we have to reckon first the entropy which water acquires in being heated, and next the entropy L₁/τ₁ which is acquired when the conversion into steam has taken place. Reckoning from any standard temperature τ₀, in the heating of the feed-water up to any temperature τ, the entropy acquired is

$\phi _{w}=\int _{\tau ^{0}}^{\tau }{\frac {\sigma d\tau }{\tau }},$

and taking σ as sensibly constant,

$\phi _{w}=\sigma (\log _{\epsilon }\tau -\log _{\epsilon }-\log _{\epsilon }\tau _{0}).$

During evaporation at τ₁ a quantity of heat L₁ is taken in at temperature τ₁, and hence the entropy of the steam

$\phi _{s}=\phi _{w}+{\text{L}}_{1}/\tau _{1}=\sigma (\log _{\epsilon }\tau _{1}-\log _{\epsilon }\tau _{0})+{\text{L}}_{1}/\tau _{1}.$

Values of the entropy of water and steam are given in the table. The entropy-temperature diagram for a Rankine cycle is illustrated in fig. 11, where 𝑎𝑏, a logarithmic curve, represents the process of heating the feed-water, and 𝑏𝑐 the passage from the state of water into that of steam. The diagram is drawn to scale for a case in which steam is formed at a pressure of 180 ℔ per sq. in., and condensed at a pressure of 1 ℔ per sq. in. After the formation of the steam, the next step in the ideal process is adiabatic expansion from the higher to the lower limit of temperature, which is represented by the vertical straight line 𝑐𝑑, an adiabatic process being also isentropic. Finally, the cycle is completed by 𝑑𝑎, which represents the condensation of the steam after its temperature has been reduced by adiabatic expansion to the lower limit of temperature. The area 𝑎𝑏𝑐𝑑 represents the work done, and its value per ℔ of steam is identical with W as reckoned above. The area 𝑚𝑎𝑏𝑐𝑝 is the whole heat taken in, and the area 𝑚𝑎𝑑𝑝 is the heat rejected.

Fig. 11

Let a curve 𝑐𝑓 be drawn to show the values of the entropy of steam for various temperatures of saturation: then if 𝑎𝑑 be produced to meet the curve in 𝑓, the ratio 𝑓𝑑/𝑓𝑎 represents the fraction of the steam which was condensed during adiabatic expansion. For the point 𝑓 represents the state of 1 ℔ of saturated steam, and in the condensation of 1 ℔ of saturated steam the heat given out would be the area under 𝑓𝑎, whereas the heat actually given out in the condensation from 𝑑 was the area under 𝑑𝑎. Thus the state at 𝑑 is that of a wet mixture in which 𝑑𝑎/𝑓𝑎 represents the fraction present as steam, and 𝑓𝑑/𝑓𝑎 the fraction present as water. It obviously follows that by drawing horizontal lines at intermediate temperatures the development of wetness in the expanding steam can be readily traced. Again, if the steam is not dry when expansion begins, its state may be represented by making the expansion line begin at a point in the line 𝑏𝑐, such that the segments into which the line is divided are proportional to the constituents of the wet mixture. In this way the ideal process may be exhibited for steam with any assumed degree of initial wetness. Further, the entropy-temperature diagram admits of ready application to the case of incomplete expansion. Suppose, for example, that after adiabatic expansion from 𝑐 to 𝑐′ (fig. 12) the steam is directly cooled to the lower-limit temperature by the application of cooling water instead of by continued expansion. This process is represented by the line 𝑐′𝑒𝑑, which is a curve of constant volume. Its form is determined by the consideration that at any point 𝑒 the proportion of steam still uncondensed, or 𝑙𝑒/𝑙𝑘, is such that the mixture fills the same volume as was filled at 𝑐′.

Fig. 12

43. Entropy-Temperature Diagrams extended to the Case of Superheated Steam.—In the diagrams which have been sketched, it has been assumed that the steam is supplied to the engine in a saturated state. To extend the same treatment to the case of superheated steam, we have to take account of the supplementary supply of heat which the steam receives after the point 𝑐 is reached, and before expansion begins. When superheating is resorted to, as is now often the case in practice, the superheat is given at constant pressure. If κ represent as before the mean specific heat of steam at constant pressure, the addition of entropy during the process of superheating from τ₁ to τ′ is κ(τ′ − τ₁). The value of κ may be treated as approximately constant, and the addition to the entropy may then be written as κ(log τ − log τ₁). This gives a line such as 𝑐𝑟 on the entropy diagram (fig. 13), and increases the value of W by the amount

$\int _{\tau _{1}}^{\tau '}{\frac {\kappa d\tau (\tau -\tau _{2})}{\tau }}$

which is represented on the diagram by the area 𝑑𝑐𝑟𝑠. During adiabatic expansion from 𝑟 the steam remains superheated until it reaches the state 𝑡, when it is just saturated, and further expansion results in the condition of wetness indicated by 𝑠. The extra work 𝑑𝑐𝑟𝑠 is done at the expense of the extra supply of heat 𝑝𝑐𝑟𝑢, and an inspection of the diagram suffices to show that the efficiency of the ideal cycle is only very slightly increased by even a large amount of superheating. In practice, however, superheating does much to promote efficiency, because it materially reduces the amount by which the actual performance of an engine falls short of the ideal performance by keeping the steam comparatively dry in its passage through the engine, and thereby reducing exchanges ot heat between the steam and the metal.

Fig. 13

44. Entropy of Wet Steam.—The entropy of wet steam is readily calculated by considering that the change of entropy in the conversion from water to steam will be 𝑞L/τ if the steam is wet, 𝑞 being the dryness Accordingly the entropy of wet steam at any temperature τ is σ(log_ετ − log_ετ₀)+𝑞L/τ. Further, since σ for water is practically equal to unity this expression may be written

φ＝log_ετ − log_ετ₀+𝑞L/τ.

We may apply this expression to trace the development of wetness in steam when it expands adiabatically. In adiabatic expansion φ＝constant. Using the suffix 1 to distinguish the initial state, we therefore have at any stage in the expansion

log_ετ − log_ετ₀＝log_ετ₁ − log_ετ₀ +𝑞₁L₁/τ₁,

from which the dryness at that stage is found, namely,

𝑞＝τ/L(𝑞₁L₁/τ₁ + log_ετ₁/τ₁).

The expression is not applicable to steam which is initially superheated. In either case the graphic method of tracing the change of condition during adiabatic expansion is available.

45. Actual Performance.—Trials of engines using saturated steam show that in the most favourable cases from 60 to 65% of the ideally possible amount of work is realized as “indicated” work One of the causes of loss is that the expansion is incomplete. In practice the steam is allowed to escape to the condenser, while its pressure is still considerably higher than the pressure at which condensation is to take place. When the pressure of steam in the cylinder has been so far reduced by expansion that it can only overcome the friction of the piston, there is no advantage in going on further; the indicated work due to any additional expansion would add nothing to the output of the engine, when allowance is made for the work spent on friction within the mechanism itself. Considerations of bulk often lead to an even earlier release of the expanding steam; and another consideration which points the same way is that when expansion is carried very far, the losses due to exchange of heat between the cylinder and the steam, referred to below, tend to increase. Again, since experience shows that the most efficient engines are those in which the process of expansion is divided into two, three or more stages by the use of compounded cylinders, a certain amount of loss is to be ascribed to the drops in pressure which are liable to occur through unresisted expansion in the transfer of steam from one vessel to another. But the chief cause of loss is to be found in the exchanges of heat which take place between the steam and the metal. In each cylinder there is a process of alternate condensation and re-evaporation—condensation during the period of admission, when the steam finds itself brought into contact with metal which has been chilled by evaporation during the preceding exhaust stroke, and then evaporation, when the pressure has fallen sufficiently, during the later stage of expansion, as well as during exhaust. The consequence is that the steam though supplied in a dry
Fig. 14 state, may contain some 20 or 30% of moisture when admission to the cylinder is complete, and the entropy diagram for the real process of expansion takes a form such as is indicated by the line 𝑐′𝑐″ in fig. 14. The heat supplied is still measured by the area under 𝑎𝑏𝑐. The condensation from 𝑐 to 𝑐′ occurs by contact with the walls of the cylinder; and though part of the heat thus abstracted is restored before release occurs at 𝑐″ , the general result is to make a large reduction in the area of the diagram.

46. Exchanges of Heat between the Steam and the Metal.—The exchanges of heat between steam and metal in the engine cylinder have been made the subject of an elaborate experimental examination by Professors Callendar and Nicolson (Proc. Inst. C.E. cxxxi. 147), who studied the cyclic variations of temperature throughout the metal by means of thermo-electric junctions set at various depths. They found that the range of temperature through which the surface of the metal fluctuates is much less than the range of temperature passed through by the steam; the processes of condensation and re-evaporation are slow, and the time is too short to bring the surface of the metal into anything like equilibrium with the steam. The amount of condensation up to the point of cut-off, as inferred from the heat which the metal takes up, may be much less than the “missing quantity” or difference between the steam supplied per stroke and the dry steam then present. According to their experiments, this discrepancy is accounted for by leakage of steam past the valve, direct from the steam chest to the exhaust, and they suggest that this source of error may have been present in many estimates of initial condensation based on determinations of the missing quantity. This may explain cases in which the initial condensation has apparently been excessive, but large amounts of initial condensation certainly do occur, and constitute the most potent factor in making the real performance of the engine fall short of the ideal standard.^[6]

In the alternate condensation and re-evaporation of steam in the cylinder more heat is given to the metal by each pound of steam that is condensed than is taken from the metal by each pound of steam that is re-evaporated, the temperature of condensation being higher than that of re-evaporation. The quantity H₁−H₂, namely, the difference in the heat of formation at the two temperatures, represents this excess of heat. Unless this is in some way abstracted from the metal, the process cannot occur. Hence the action of the cylinder walls in causing alternate condensation and re-evaporation to occur may be limited by imposing conditions which prevent or reduce the abstraction of heat. By the use of a steam jacket the metal may be prevented from losing heat externally, and may even be made to take up heat. Under these conditions the action depends on the fact that more water is re-evaporated than is condensed. To some extent this is a necessary result of the work done during expansion, which (in an adiabatic process) would make the steam become wetter as expansion proceeds, and would therefore leave more water to be evaporated than is initially condensed by the action of the cylinder walls. But it is important to notice that any water which is introduced into the cylinder along with the steam will be an important factor in supplying the means by which this thermal balance is maintained. With steam that is perfectly dry before admission the action of the walls takes its limit from the condensation which expansion brings about; with steam that is wet before admission no such limit applies. Hence the importance of having steam that is initially dry. To secure this, no method is so certain as to give some initial superheat to the steam, and hence arises the practical advantage which even a small amount of superheating is found to bring about.

47. Influence of the Slide-Valve.—To a considerable extent the slide-valve itself promotes initial condensation, for it requires that the hot steam shall enter the cylinder through a passage which, immediately before, was chilled by being used for the escape of exhaust steam. The use of entirely distinct admission and exhaust ports and valves tends towards economy of steam, partly for this reason and partly because it allows the clearance spaces to be reduced. Accordingly, we find that many of the best recorded results of tests relate to engines in which each cylinder has four separate valves of the Corliss or of the drop type. By using horizontal cylinders with admission valves on the top and exhaust valves below, the further advantage of drainage through the exhaust valves is secured. Water which is present at release has then the chance of escaping without being re-evaporated, a circumstance which contributes largely to reduce the exchange of heat between the working substance and the metal. Thus a horizontal triple-expansion engine with drop valves, by Messrs Sulzer, using saturated steam at an absolute pressure of 160 ℔ per sq. in., and indicating not much more than 200 h.p., is reported, in a test by Professor Stodola, to have used only 11·52 ℔ of steam per indicated horse-power-hour (see Engineer, July 1, 1898; also summary of trials by B. Donkin, ibid., Oct. 13, 1899). The performance in this test is equivalent to nearly 69% of the ideal, an exceptionally high figure. In one or two trials of larger engines even this performance has been surpassed, 11·2 and 11·3 ℔ per horse-power-hour having been recorded. In other particularly favourable records of trials the consumption of steam with triple-expansion engines has been found to lie between 12 and 13 ℔ per horse-power-hour. Some of the best results relate to slow-running pumping engines fitted with steam jackets on the barrels and on the covers of the cylinders, and may be taken as showing how influential, in a long-period engine, the jacket may prove in reducing the evils of initial condensation. In the mean of several apparently authoritative trials by different observers on different engines the consumption of steam was 12·2 ℔ per horse-power-hour, at an absolute pressure of about 140 ℔ per sq. in., which corresponds to 66% of the ideal performance. It should be added that these figures are exceptional. A consumption of 13 or 14 ℔ of steam per horse-power-hour is much more usual even in large and well-designed triple-expansion engines; and with two-cylinder compound engines, using steam with an absolute pressure of 100 or 120 ℔ per sq. in., anything from 14 to 15 ℔ may be reckoned a good performance.

48. Superheated Steam.—The advantage of superheated steam, which arises mainly from its influence in reducing the exchange of heat between the steam and cylinder walls, was demonstrated by the experiments of Hirn, and as early as 1860 it was not unusual to supply superheaters with marine engines. But the practice of superheating was soon abandoned, chiefly on account of difficulties in regard to lubrication. By the introduction of heavy mineral oils this objection has been removed, and a revival in the use of superheating has taken place, with striking effect on the thermodynamic economy of engines. Experiments made in 1892 by the Alsatian Society of Steam Users on a large number of engines showed that superheating effected an average saving in coal to the extent of about 20%, when the superheater was simply placed in the boiler flue, so that it utilized what would otherwise be waste heat, and about 12% when the superheater was separately fired. In those cases the steam was superheated only about 30° to 45° C. above the temperature of saturation, but in more recent practice much greater amounts of superheat have been successfully applied. Professor Schroter has tested a factory engine of 1000 h.p., using steam superheated by some 50° C., and has shown that this amount of superheat is not sufficient to prevent some of the steam from becoming condensed on the walls during admission to the cylinder (Zeitschrift des Vereins deutscher Ingenieure, vol. xl., 1896). It follows that still larger amounts of superheat will be thermodynamically advantageous. That this is the case has been demonstrated by the remarkable results which have been obtained with highly superheated steam by W. Schmidt in stationary engines and locomotives. Using a somewhat special design, Schmidt has shown that it is perfectly practicable to employ steam superheated to a temperature of 400° C., and that an efficiency not attainable from steam in any other way is thereby reached. In several authentic trials of Schmidt engines the consumption of steam has been considerably less than 10 ℔ per indicated horse-power-hour—a figure which, after allowance is made for the heat taken up during the process of superheating, represents a better performance than that of the best engines using saturated or slightly superheated steam. It has been found that the consumption of coal, in the boiler and superheater together, need not exceed 11/3 ℔ per indicated horse-power even with engines of small power. To attain this remarkable result it is of course necessary that, after the hot gases from the furnace have passed the superheater, a further extraction of heat from them should take place. This is done by an economizer or feed-water heater of peculiar form, consisting of a long coil of small pipes which maintain a circulation of hot distilled water through a closed system containing an external coil, which forms the heater of a tank through which the feed-water passes on its way to the boiler. Some of the Schmidt engines adopt the principle of single action, to escape the necessity of having a piston-rod and gland on the side which is exposed to contact with high-temperature steam; but it is found that this precaution is not essential, and that with glands of suitable design a double-acting piston may be used without inconvenience, and without risk of undue wear. In some instances Schmidt transfers to the partially expanded steam in the intermediate receiver a portion of the heat which is conveyed to the engine by the highly superheated steam; and when this is done, the steam may properly receive a still higher degree of initial superheat. Accordingly, though the initial temperature of the steam may be 400° C. or more, this is reduced to about 320 by transfer to steam in the superheater before the high-pressure steam is admitted to the cylinder. In tests by the present writer of a Schmidt plant indicating 180 h.p., in which this device was employed, the steam was superheated to 397° C. and 10·4 ℔ were used per horse-power-hour. In this trial the temperature of the chimney gases was reduced, by the use of Schmidt’s feed-water heater, to 175° C, and the consumption of coal was 1·31 ℔ per indicated horse-power-hour. In another trial, of a larger engine with steam superheated to 425° C, the consumption of steam per horse-power-hour was only 9·0 ℔.

49. The Indicator.—The actual behaviour of steam in the cylinder of a steam engine is studied by means of the indicator, which serves not only to measure the work done but to examine the operation of the valves and generally to give much useful information regarding the action of the engine. The indicator, which was invented by Watt, and improved by Richards, is a device for automatically drawing a diagram showing the pressure at all points of the piston’s stroke. In its most usual form it consists of a small steam cylinder fitted with a piston which slides easily within it and is pressed down by a spiral spring of steel wire. The cylinder of the indicator is connected by a pipe below this piston to one or other end of the cylinder of the engine, so that the piston of the indicator rises and falls in response to the fluctuations of pressure which occur in the engine cylinder. The indicator piston actuates a pencil, which rises and falls with it and traces the diagram on a sheet of paper fixed to a drum that is caused to rotate back and forth through a certain arc, in unison with the motion of the engine piston. In M‘Naught’s indicator the pencil is directly attached to the indicator piston, in Richards’s the pencil is moved by means of a system of links so that it copies the motion of the piston on a magnified scale. This has the advantage that an equally large diagram is drawn with much less movement of the piston, and errors which are caused by the piston’s inertia are consequently reduced. In high-speed engines especially it is important to minimize the inertia of the indicator piston and the parts connected with it. In Richards’s indicator the linkage employed to multiply the piston’s motion is an arrangement similar to the parallel motion introduced by Watt as a means of guiding the piston-rod in beam engines. In several recent forms of indicator lighter linkages are adopted, and other changes have been made with the object of fitting the instrument better for high-speed work. One of these modified forms of Richards’s indicator (the Crosby) is shown in fig. 15.

Fig. 15.—Crosby Indicator.

The pressure of steam in the engine cylinder raises the piston P, compressing the spring S and causing the pencil Q to rise in a nearly straight line through a distance proportional, on a magnified scale, to the compression of the spring and therefore to the pressure of the steam. At the same time the drum D, which carries the paper, receives motion through the cord C from the crosshead of the engine. Inside this drum there is a spiral spring which becomes wound up when the cord is pulled, and serves to turn the drum in the reverse direction during the back stroke. The cap of the indicator cylinder has holes in it which admit air freely to the top of the piston, and the piston has room to descend, extending the spring S, when the pressure of the steam is less than that of the atmosphere. The spring is easily taken out and replaced by a more or less stiff one when higher or lower pressures have to be dealt with.

50. Errors in Indicator Diagrams.—To register correctly, an indicator must satisfy two conditions: (1) the motion of the piston must be proportional to the change of steam pressure in the engine cylinder: and (2) the motion of the drum must be proportional to that of the engine piston.

The first of these requires that the pipe which connects the indicator with the cylinder should be short and of sufficient bore, and that it should open in the cylinder at a place where the pressure in it will not be affected by the kinetic action of the inrushing steam. Frequently pipes are led from both ends of the cylinder to a central position where the indicator is set, so that diagrams may be taken From either end without shifting the instrument; better results are obtained, especially when the cylinder is long, by using a pair of indicators, each fixed with the shortest possible connecting pipe. The general effect of an insufficiently free connexion between the indicator and the engine cylinder is to make the diagram too small. The first condition is also invalidated to some extent by the friction of the indicator piston, of the joints in the linkage, and of the pencil on the paper. The piston must slide very freely; nothing of the nature of packing is permissible, and any steam that leaks past it must have a free exit through the cover. The pencil pressure must not exceed the minimum which is necessary for clear marking. Another source of disturbance is the inertia of the moving parts, which tends to set them into oscillation whenever the indicator piston suffers a comparatively sudden displacement. These oscillations, superposed upon the legitimate motions of the piston, give a wavy outline to parts of the diagram, especially when the speed is great. When they appear on the diagram a continuous curve should be drawn midway between the crests and hollows of the undulations. To keep them within reasonable compass in high-speed work a stiff spring must be used and an indicator with light parts should be selected. Care must be taken that the spring is graduated to suit the temperature (about 100° C.) to which it is exposed when in use;. its stiffness at this temperature is about 3% less than when cold.

51. Measurement of Horse-Power.—To determine the indicated horse-power, the mean effective pressure is found by dividing the area of the diagram by the length of its base. This gives a mean height, which, interpreted on the scale of pressures, is the mean effective pressure in pounds per square inch., This has to be multiplied by the effective area of the piston in square inches and by the length of the piston stroke in feet to find the work done per stroke in foot-pounds on that side of the piston to which the diagram refers. Let A₁ be the area of the piston on one side and A₂ on the other; 𝑝₁ and 𝑝₂ the mean effective pressures on the two sides respectively; L the length of the stroke in feet; and 𝑛 the number of complete double strokes or revolutions per minute. Then the indicated horse-power

I.H.P.＝𝑛L(𝑝₁A₁+𝑝₂A₂)/33000.

In finding the mean pressure the area of the diagram may be conveniently measured by a planimeter. A less accurate plan, frequently followed, is to divide the diagram by lines drawn at the middle of strips of equal width and to take the mean pressure as the average height of these lines.

52. Tests of Efficiency.—In testing the actual efficiency of an engine the work done as determined by the indicator is compared with the supply of heat, which is calculated from the amount of steam passing through the engine. We may find the amount of steam passing through either by measuring the feed-water or, when a surface condenser is used, by collecting the condensed water from the air-pump discharge and measuring that, adding the water drained from jackets if any are used. In some trials both of these measurements have been made, and it has been found that in general the amount of feed-water exceeds the amount of steam discharged from air-pump and jackets by something like 3 or 4%, a discrepancy due to leakages in the boiler and the engine. The results of tests are generally stated by giving the number of pounds of steam used per horse-power-hour, or by giving the work done by each pound of steam, a quantity which is directly comparable with the amount of work ideally obtainable, if the engine followed the perfect Rankine cycle already discussed. To make a complete engine trial the engine is caused to work not only at full power, but at various fractions of its greatest load. The results are very conveniently represented (in a manner due to P. W. Willans) by drawing a curve, the co-ordinates of which are the horse-power and the total consumption of steam per hour. This “Willans Line,” as it is called, is in most cases straight or nearly straight. Another useful curve is drawn by plotting the steam used per horse-power-hour in relation to the horse-power.

53. Determination of the “Missing Quantity.”—When the amount of steam passing through the engine is known, the indicator diagram enables the degree of wetness of the steam to be estimated at various stages in the expansion from cut-off to release, provided there is no direct passage from steam-chest to exhaust, such as has been referred to above in connexion with Messrs Callendar and Nicolson’s researches. For this purpose we must first calculate the quantity of the working substance present in the cylinder. It is made up of two parts, namely, the amount supplied per stroke, plus the amount retained by being shut up in the clearance space. If we assume, as may generally be done without serious error, that at the beginning of compression the steam present in the cylinder is dry, it is an easy matter to deduce from the diagram, knowing the pressure and the volume, how much steam is shut up in the clearance. Adding that to the supply per stroke, we get the whole quantity that is present from cut-off to release. The volume which this would occupy at each pressure, if saturated, is found from the steam table. The volume actually occupied at each pressure is found from the diagram, and by comparing the two it is easy to infer how much of the substance exists as water and how much as steam. The ratio of the two volumes measures with sufficient accuracy the dryness of the steam. Any direct leakage from the steam side to the exhaust side of the valve will invalidate this calculation, which proceeds. On the basis that all the steam passing through the engine passes through the cylinder.

54. Compound Engines.—In the original form of compound engine, invented by Hornblower and revived by Woolf, steam passed directly from the first to the second cylinder; the exhaust from the first and admission to the second went on together throughout the whole of the back stroke. This arrangement is possible only when the high and low pressure pistons begin and end their strokes together, as in engines of the “tandem” type, whose high and low pressure cylinders are in one line, with one piston-rod common to both pistons. Engines in which the high and low pressure cylinders are placed side by side, and act either on the same crank or on cranks set at 180° apart, may also discharge steam directly from one to the other cylinder; the same remark applies to beam engines, whether of the class in which both pistons act on one end of the beam, or of the class introduced by M‘Naught, in which the high and low pressure cylinders stand on opposite sides of the centre. By a convenient usage which is now pretty general the name “Woolf engine” is restricted to those compound engines which discharge steam directly from the high to the low pressure cylinders without the use of an intermediate receiver.

55. Receiver Engine.—An intermediate receiver becomes necessary when the phases of the pistons in a compound engine do not agree With two cranks at right angles, for example, a portion of the discharge from the high-pressure cylinder occurs at a time when the low-pressure cylinder cannot properly receive steam. The receiver is in some cases an entirely independent vessel connected to the cylinders by pipes; very often, however, a sufficient amount of receiver volume is afforded by the valve casings and the steam pipe which connects the cylinders. The receiver, when it is a distinct vessel, is frequently jacketed.

A receiver is frequently applied with advantage to beam and tandem compound engines Communication need not then be maintained between the high and low pressure cylinders during the whole of the stroke, admission to the low-pressure cylinder is stopped before the stroke is completed; the steam already admitted is allowed to expand independently; and the remainder of the discharge from the high-pressure cylinder is compressed into the intermediate receiver. Each cylinder has then a definite point of cut-off, and by varying these points the distribution of work between the two cylinders may be adjusted at will. In general it is desirable to make both cylinders of a compound engine contribute equal quantities of work. If they act on separate cranks this has the effect of giving the same value to the mean twisting moment of both cranks.

56. Compound Diagrams.—Wherever a receiver is used, care should be taken that there should not be a wasteful amount of unresisted expansion into it; in other words, the pressure in the receiver should be not greatly less than that in the high-pressure cylinder at the moment of release. If the receiver pressure is less there will be what is termed “drop” in the steam pressure between the high-pressure cylinder and the receiver, which will show itself in an indicator diagram by a sudden fall at the end of the high-pressure expansion. This “drop” is, from the thermodynamic point of view, irreversible, and therefore wasteful. It can be avoided by selecting a proper point of cut-off in the low-pressure cylinder. When there is no “drop” the expansion that occurs in a compound engine has precisely the same effect in doing work as the same amount of expansion in a simple engine would have, provided the law of expansion be the same in both and the waste of energy which occurs by the friction of ports and passages in the transfer of steam from one to the other cylinder be negligible. The work done in either case depends merely on the relation of pressure to volume throughout the process; and so long as that relation is unchanged it is a matter of indifference whether the expansion be performed in one vessel or in more than one. In general a compound engine has a thermodynamic advantage over a simple engine using the same pressure and the same expansion, inasmuch as it reduces the exchange of heat between the working substance and the cylinder walls and so makes the process of expansion more nearly adiabatic. The compound engine has also a mechanical advantage which will be presently described. The ultimate ratio of expansion in any compound
Fig. 16.—Compound Diagrams:
Woolf type. engine is the ratio of the volume of the low-pressure cylinder to the volume of steam admitted to the high-pressure cylinder. Fig. 16 illustrates the combined action of the two cylinders in a hypothetical compound engine of the Woolf type, in which for simplicity the effect of clearance is neglected and also the loss of pressure which the steam undergoes in transfer from one to the other cylinder. ABCD is the indicator diagram of the high-pressure cylinder. The exhaust line CD shows a falling pressure in consequence of the increase of volume which the steam is then undergoing through the advance of the low-pressure piston. EFGH is the diagram of the low-pressure cylinder drawn alongside of the other for convenience in the construction which follows. It has no point of cut-off; its admission line is the continuous curve of expansion EF, which is the same as the high-pressure exhaust line CD, but drawn to a different scale of volumes. At any point K, the actual volume of the steam is KL + MN. By drawing OP equal to KL + MN, so that OP represents the whole volume, and repeating the same construction at other points of the diagram, we may set out the curve QPR, the upper part of which is identical with BC, and so complete a single diagram which exhibits the equivalent expansion in a single cylinder.

In a tandem compound engine of the receiver type the diagrams resemble those shown in fig. 17. During CD (which corresponds to FG) expansion is taking place into the large or low-pressure
Fig. 17.—Compound Diagrams: Receiver type. cylinder. D and G mark the point of cut-off in the large cylinder, after which GH shows the independent expansion of the steam now shut within the large cylinder, and DE shows the compression of steam by continued discharge from the small cylinder into the receiver. At the end of the stroke the receiver pressure is OE, and if there is to be no “drop,” this must be the same as the pressure at C. Diagrams of a similar kind may be sketched without difficulty for the case of a receiver engine with any assigned phase relation between the pistons.

57. Adjustment of Work and “Drop.”—By making the cut-off take place earlier in the large cylinder we increase the mean pressure in the receiver; the work done in the small cylinder is consequently diminished. The work done in the large cylinder is correspondingly increased, for the total work (depending as it does on the initial pressure and the total ratio of expansion) is unaffected by the change. The same adjustment serves, in case there is “drop,” to lessen it. By selecting a suitable ratio of cylinder volumes to one another and to the volume of the receiver, and also by choosing a proper point for the low-pressure cut-off, it is possible to divide the work suitably between the cylinders and at the same time prevent the amount of drop from being greater than is practically convenient.

58. Uniformity of Effort in a Compound Engine.—An important mechanical advantage belongs to the compound engine in the fact that it avoids the extreme thrust and pull which would have to be borne by the piston-rod of a single-cylinder engine working at the same power with the same initial pressure and the same ratio of expansion. If all the expansion took place in the low-pressure cylinder, the piston at the beginning of the stroke would be exposed to a thrust much greater than the sum of the thrusts on the two pistons of a compound engine in which a fair proportion of the expansion is performed in the small cylinder. The mean thrust throughout the stroke in a tandem engine is of course not affected by compounding; only the range of variation in the thrust is reduced. The effort on the crank-pin is consequently made more uniform, the strength of the parts may be reduced, and the friction at slides and journals is lessened. The advantage in this respect is obviously much greater when the cylinders are placed side by side, instead of tandem, and work on cranks at right angles. As a set-off to its advantage in giving a more uniform effort, the compound engine has the drawback of requiring more working parts than a simple engine with one cylinder. But in many instances—as in marine engines—two or more Cranks are almost indispensable to give a tolerably uniform effort' and to get over the dead points; and the comparison should then be made between a pair of simple cylinders and a pair of compounded cylinders. Another point in favour of the compound engine is that, although the whole ratio of expansion is great, there need not be a very early cut-off in either cylinder; hence the common slide-valve, which is unsuited to give an early cut-off, may be used in place of a more complex arrangement. The mechanical advantage of the compound engine has long been recognized, and had much to do with its adoption in the early days of high-pressure steam. Its subsequent development has been due in part to this, and in part to the thermodynamic advantage which has been discussed above.

59. Ratio of Cylinder Volumes.—In a two-cylinder compound engine, using steam at 80 to 100 ℔ pressure, the large cylinder has 3 or 4 times the volume of the small cylinder. In triple engines the pressure is rarely less than 150 ℔; the low-pressure cylinder has generally 6 or 7 times, and the intermediate cylinder 21/2 to 23/4 times the volume of the high-pressure cylinder. In naval practice the ratios are about 1 : 21/4 : 5 for a pressure of 160 ℔ and 1 : 2·6 : 7 for a pressure of 250 ℔. In the mercantile marine the engines are normally working at full power, whereas in the navy most of the working is at greatly reduced powers, the cruising speed requiring very much less than the full output. Consequently, for the same boiler pressure, the cylinder ratio is made less in war-ships to adapt the engines for economical working under cruising conditions.

Fig. 18.—Horizontal Section through Cylinder and Valve-chest:
showing Slide-valve.

60. The Distribution of Steam.—In early steam engines the distribution of steam was effected by means of conical valves, worked by tappets from a rod which hung from the beam. The slide-valve, the invention of which in the form now known as the long D-slide is credited to Murdock, an assistant of Watt, came into general use with the introduction of locomotives, and is now employed, in one or other of many forms, in the great majority of engines.

The common slide-valve is illustrated in fig. 18, which also shows the cylinder and the ports and passages leading to its ends. The seat, or surface on which the valve slides, is a plane surface formed on or fixed to the side of the cylinder, with three ports or openings which extend across the greater part of the cylinder’s width. The central opening is the exhaust port through which the steam escapes; the others, or steam ports, which are narrower, lead to the two ends of the cylinder respectively. The valve is a box-shaped cover which slides over the seat, and the whole is enclosed in a chamber called the valve-chest, to which steam from the boiler is admitted. When the valve moves a sufficient distance to either side of the central position, steam enters one end of the cylinder from the valve-chest and escapes from the other end of the cylinder through the cavity of the valve into the exhaust port. The valve is generally moved by an eccentric on the engine shaft, which is mechanically equivalent to a crank whose radius is equal to the
Fig. 19. eccentricity, or distance from the centre of the shaft to the centre of the eccentric sheave. The eccentric rod is generally so long that the motion of the valve is sensibly the same as that which it would receive were the rod infinitely long. Thus if a circle (fig. 19) be drawn to represent the path of the eccentric centre during a revolution of the engine, and a perpendicular PM be drawn from any point P on a diameter AB, the distance CM is the displacement of the valve from its middle position at the time when the eccentric centre is at P. AB is the whole travel of the valve.

61. Lap and Lead.—If the valve when in its middle position did not overlap the steam ports (fig. 20), any movement to the right or the left would admit steam, and the admission would continue until the valve had returned to its middle position, or, in other words, for half a revolution of the engine. Such a valve would not serve for expansive working, and as regards the relative position of the crank and eccentric it would have to be set so that its middle position coincided with the extreme position of the piston; in other words, the eccentric radius would make a right angle with the crank.


Fig. 20.—Slide-Valve without Lap.		Fig. 21.—Slide-Valve with Lap.

Expansive working, however, becomes possible when we give the valve what is called “lap,” by making it project over the edges of the steam ports, as in fig. 21, where is the “outside lap” and 𝑖 is the “inside lap.” Admission of steam (to either side) then begins only when the displacement of the valve from its middle position exceeds the amount of the outside lap, and continues only until the valve has returned to the same distance from its middle position. Further, exhaust begins only when the valve has moved past the middle by a distance equal to 𝑖, and continues until the valve has again returned to a distance 𝑖 from its middle position. Thus on the diagram of the eccentric’s travel (fig. 22) we find, by setting off 𝑜 and 𝑖
Fig. 22. on the two sides of the centre, the positions 𝑎, 𝑏, 𝑐 and 𝑑 of the eccentric radius at which the four events of admission, cut-off, release and compression occur for one side of the piston. As to the other side of the piston, it is only necessary to set off 𝑜 to the right and 𝑖 to the left of the centre, but for the sake of clearness we may confine our attention to one of the two sides. Of the whole revolution, the part from 𝑎 to 𝑏 is the arc of steam admission, from 𝑏 to 𝑐 is the arc of expansion, from 𝑐 to 𝑑 the arc of exhaust, and from 𝑑 to 𝑎 the arc of compression. The relation of these, however, to the piston’s motion is still undefined. If the eccentric were set in advance of the crank by an angle equal to AC𝑎, the opening of the valve would be coincident with the beginning of the piston’s stroke. It is, however, desirable, in order to allow the steam free entry, that the valve be already some way open when the piston stroke begins, and thus the eccentric may be set to have a position C𝑎′ at the beginning of the stroke. In that case the valve is open at the beginning of the stroke to the extent 𝑚𝑚′, which is called the “lead.” The amount by which the angle between C𝑎′ (the eccentric) and CA (the crank) exceeds a right angle is called the angular advance, this being the angle by which the eccentric is set in advance of the position it would occupy if the primitive arrangement without lap were adopted. The quantities lap, lead and angular advance (θ) are connected by the equation

outside lap＋lead＝half travel ✕ cos θ.

An effect of lead is to cause preadmission, that is to say, admission before the end of the back stroke, which, together with the compression of steam left in the cylinder when the exhaust port closes, produces the mechanical effect of “cushioning,” to which reference has already been made. To examine the distribution of steam throughout the piston’s stroke, we may now draw a circle to represent the path of the crank pin (fig. 23, where the dotted lines have been added to show the assumed configuration of piston, connecting-rod and crank) and transfer to it from the former diagram the angular positions 𝑎, 𝑏, 𝑐 and 𝑑 at which the four events occur.

Fig. 23.

To facilitate this transfer the diagrams of eccentric path and of crank-pin path may by a suitable choice of scales be drawn of the same actual size. Then by projecting these points on a diameter which represents the piston’s path, by circular arcs drawn with a radius equal to the length of the connecting-rod, we find 𝑝, the position of the piston at which admission occurs during the back stroke, also 𝑞 and 𝑟, the position at cut-off and release, during the stroke which takes place in the direction of the arrow, and 𝑠, the point at which compression begins. It is obviously unnecessary to draw the two circles of figs. 22 and 23 separately; the single diagram (fig. 24) contains the solution of the steam distribution with a slide-valve whose laps, travel and angular advance are known, the same circle serving, on two scales, to show the motion of the crank and of the eccentric.


Fig. 24.		Fig. 25.

Zeuner’s Diagram.—The graphic construction most usually employed in slide-valve investigations is the ingenious diagram published by Dr G. Zeuner in the Civilingenieur in 1856.^[7] On the line AB (fig. 25), which represents the travel of the valve, let a pair of circles (called valve-circles) be drawn, each with diameter equal to the half travel. A radius vector CP, drawn in the direction of the eccentric at any instant, is cut by one of the circles at Q, so that CQ represents the corresponding displacement of the valve from its middle position. That this is so will be seen by drawing PM (as in fig. 19) and joining QB, when it is obvious that CQ＝CM, which is the displacement of the valve. The line AB with the circle on it may now be turned back through an angle of 90°+θ (θ being the angular advance), so that the valve-circles take the position shown to a larger scale in fig. 26.

Fig. 26.—Zeuner’s Slide-Valve Diagram.

This makes the direction of CQ (the eccentric) coincide on the paper with the simultaneous direction of the crank, and hence to find the displacement of the valve at any position of the crank we have only to draw CQ in fig. 26 parallel to the crank, when CQ represents the
Fig. 27. displacement of the valve to the scale on which the diameter of each valve circle represents the half-travel of the valve. CQ₀ is the valve displacement at the beginning of the stroke shown by the arrow. Draw circular arcs 𝑎𝑏 and 𝑐𝑑 with C as centre and with radii equal to the outside lap and the inside lap 𝑖 respectively. C𝑎 is the position of the crank at which preadmission occurs. The lead is 𝑎₀Q₀. The greatest steam opening is 𝑎₁B. The cut-off occurs when the crank has the direction C𝑏. C𝑐 is the position of the crank at release, and C𝑑 marks the end of the exhaust.

63. In this diagram radii drawn from C mark the angular positions of the crank and their intercepts by the valve circles determine the corresponding displacement of the valve. It remains to find the corresponding displacement of the piston. For this Zeuner employs a supplementary graphic construction, shown in fig. 27. Here 𝑎𝑏 or 𝑎′𝑏′ represents the connecting rod, and 𝑏𝑐 or 𝑏′𝑐 the crank. With centre 𝑐 and radius 𝑎𝑐 a circle 𝑎𝑝 is drawn, and with centre 𝑏 and radius 𝑎𝑏 another circle 𝑎𝑞. Then for any position of the crank, as 𝑐𝑏′, the intercept 𝑝𝑞 between the circles is easily seen to be equal to 𝑎𝑎′, and is therefore the distance by which the piston has moved from its extreme position at the beginning of the stroke. In practice this diagram is combined with that of fig. 26, by drawing both about the same centre and using different scales for valve and piston travel A radius vector drawn from the centre parallel to the crank in any position then shows the valve’s displacement from the valve’s middle position by the intercept CQ of fig. 26, and the piston’s displacement from the beginning of the piston’s motion by the intercept 𝑝𝑞 of fig. 27.

64. In the figures which have been sketched the events refer to the front end of the cylinder, that is, the end nearest to the crank (see fig. 23). To determine the events of steam distribution at the back end, the lap circles shown by dotted lines in fig. 26 must also be drawn, C𝑎′ being the outside lap for the back end, and C𝑐′ the inside lap. These laps are not necessarily equal to those at the other end of the valve. From the diagrams it will be seen that, especially with a short connecting-rod, the cut-off and release occur earlier and the compression later at the front than at the back end if the laps are equal, and a more symmetrical steam distribution can be produced by making the inside lap greater and the outside lap less on the side which leads to the front end of the cylinder On the other hand, an unsymmetrical distribution may be desirable as in a vertical engine, where the weight of the piston assists the steam during the down-stroke and resists it during the up-stroke and this may be secured by a suitable inequality in the laps

65. By varying the ratio of the laps 𝑜 and 𝑖 to the travel of the valve, we produce effects on the steam distribution which are readily traced by means of the diagram. Reduction of travel (which is equivalent to increase of both 𝑜 and 𝑖) gives later preadmission, earlier cut-off, later release and earlier compression; the ratios of expansion and of compression are both increased. Increase of angular advance accelerates all the events and causes a slight increase in the ratio of expansion.

66. In designing a slide-valve the breadth of the steam ports in the direction of the valve’s motion is determined with reference to the volume of the exhaust steam to be discharged in a given time the area of the ports being generally such that the mean velocity of the steam during discharge is less than 100 ft. per second The travel is made great enough to keep the cylinder port fully open during the greater part of the exhaust; for this purpose it is 21/2 or 3 times the breadth of the steam port. To facilitate the exit of steam the inside lap is always small, and is often wanting or even negative. During admission the steam port is rarely quite uncovered, especially if the outside lap is large and the travel moderate. Large travel has the advantage of giving freer ingress and egress of steam, with more sharply-defined cut-off, compression and release but this advantage is secured at the cost of more work spent in moving the valve and more wear of the faces. To lessen the necessary travel without reducing the area of steam ports, double-ported valves are often used. An example is shown below in fig. 39.

67. Reversal of Motion with Slide-Valve.—The eccentric must stand in advance of the crank by the angle 90° + θ, as in fig. 28, where CK is the crank, and CE the corresponding position of the eccentric when the engine is running in the direction of the arrow 𝑎. To set the engine
Fig. 28. in gear to run in the opposite direction (𝑏) it is only necessary to shift the eccentric into the position CE′ when it will still be 90° + θ in advance of the crank. In the older engines this reversal was effected by temporarily disengaging the eccentric-rod from the valve-rod, working the valve by hand until the crank turned back through an angle equal to ECE′, the eccentric meanwhile remaining at rest, and then re-engaging the gear. instead of being keyed to the shaft, fixed to the shaft, which abutted on shoulders projecting from the sheave. reversing gear means are provided for turning the eccentric round on the shaft, but the arrangement known as the link-motion is now the most usual gear in locomotive, marine, winding and other engines which require to be often and easily reversed.

68. Link-Motion.—In the link-motion two eccentrics are used, and the ends of their rods are connected by a link. In Stephenson’s link-motion—the earliest and still the most usual form—the link is a slotted bar or pair of bars curved to the same radius as the eccentric rods (fig. 29), and capable of being shifted up or down by a suspension rod. The valve-rod ends in a block which slides within the link, and when the link is placed so that this block is nearly in line with the forward eccentric rod (R. fig. 29) the valve moves in nearly the same way as if it were driven directly by a single eccentric.

Fig. 29.—Stephenson’s Link-Motion.

This is the position of “full forward gear.” In “full backward gear,” on the other hand, the link is pulled up until the block is in nearly a line with the backward eccentric rod R′. The link-motion thus gives a ready means of reversing the engine—but it does more than this. By setting the link in an intermediate position the valve receives a motion nearly the same as that which would be given by an eccentric of shorter radius and of greater angular advance, and the effect is to give a distribution of steam in which the cut-off is earlier than in full gear, and the expansion and compression are greater. In mid gear the steam distribution is such that scarcely any work is done in the cylinder. The movement of the link, is effected by a hand-lever, or by a screw, or (in large engines) by an auxiliary steam engine. A usual arrangement of hand-lever, sketched in fig. 29, has given rise to the phrase “notching up,” to describe the setting of the link to give a greater degree of expansion.

Fig. 30.—Gooch’s Link-Motion.

Fig. 31.—Allan’s Link-Motion.

In Gooch’s link-motion (fig. 30) the link is not moved up in shifting from forward to backward gear, but a radius rod between the valve-rod and the link (which is curved to suit this radius rod) is raised or lowered—a plan which has the advantage that the lead is the same in all gears. In Allan’s motion (fig. 31) the change of gear is effected partly by shifting the link and partly by shifting a radius rod, and the link is straight.

69. Graphic Solution of Link-Motion.—The movement of a valve driven by a link-motion may be very fully and exactly analysed by drawing with the aid of a template the positions of the centre line of the link corresponding to a number of successive positions of the crank. Thus, in fig. 32, two circular arcs passing through 𝑒 and 𝑒′ are drawn with E and E′ as centres and the eccentric rods are radii. These are loci of two known points of the link, and a third locus is the circle 𝑎 in which the point of suspension must lie. By placing on the paper a template of the link, with these three points marked

on it, the position of the link is readily found, and by repeating the process for other positions of the eccentrics a diagram of positions (fig. 32) is drawn for the assigned state of the gear. A line AB drawn across this diagram in the path of the valve’s travel determines the displacements of the valve, and enables the oval diagram to be drawn, which is shown to a larger scale in another part of fig. 32. The example refers to Stephenson’s link-motion in nearly full forward gear; with obvious modification the same method may be used in the analysis of Gooch’s or Allan’s motion.

Fig. 32.

The same diagram determines the amount of slotting or sliding motion of the block in the link. In a well-designed gear this sliding is reduced to a minimum for that position of the gear in which the engine runs most usually. In marine engines the suspension-rod is generally connected to the link at the end of the link next the forward eccentric, to reduce this sliding when the engine is in forward gear.

70.—Radial Gears.—Many forms of gear for reversing and for Varying expansion have been devised with the object of escaping the
Fig. 33.—Hackworth’s Valve-Gear. use of two eccentrics, and in some both eccentrics are dispensed with. Hackworth’s gear, the parent of several others, to which the general name of radial gears is applied, has a single eccentric E (fig. 33) opposite the crank, with an eccentric-rod EQ, whose mean position is perpendicular to the travel of the valve. The rod ends in a block Q, which slides on a fixed inclined guide-bar or link, and the valve-rod receives its motion through a connecting rod from an intermediate point P of the eccentric-rod, the locus of which is an ellipse. To reverse the gear the guide-bar is tilted over to the position shown by the dotted lines, and intermediate inclinations give various degrees of expansion without altering the lead. The steam distribution is quite satisfactory, but an objection to the gear is the wear of the sliding-block and guide. In Bremme’s or Marshall’s form this objection is obviated with some loss of symmetry in the valve’s motion by constraining the motion of the point Q, not by a sliding-guide, but a suspension-link, which makes the path of Q a circular arc instead of a straight line; to reverse the gear the centre of suspension R of this link is thrown over to the position R′ (fig. 34). In the example sketched P is beyond Q, but P may be between Q and the crank (as in fig. 33), in which case the eccentric is set at 180° from the crank. This gear has been applied in a number of marine engines. In Joy’s gear, which is extensively used in locomotives, no eccentric is required; and the rod corresponding to the eccentric rod in Hackworth’s gear receives its motion from a point in the connecting rod by the linkage shown in fig. 35, and is either suspended, as in Marshall’s form, by a rod whose suspension centre R is thrown over to reverse the motion, or constrained, as in Hackworth’s, by a slot-guide whose inclination is reversed. Fig. 36 shows Joy’s gear as applied to a locomotive. A slot-guide E is used, and it is curved to allow for the obliquity of the valve connecting-rod AE. C is the crank-pin, B the piston path and D a fixed centre.

A form of radial gear very largely used in locomotives, especially on the continent of Europe, is the Walschaert or Heusinger-Waldegg gear, in which the valve receives its motion in part from the piston cross-head through a reducing lever, and in part from a single eccentric set at right angles to the crank, which actuates a rocking link. Reversing is effected by shifting a sliding block along this rocking link from one side to the other of the centre on which it rocks.

Fig. 34.—Bremme’s or Marshall’s Valve-Gear.

71. Separate Expansion-Valves.—When the distribution of steam is effected by the slide-valve alone the arc of the crank’s motion during which compression occurs is equal to the arc during which expansion occurs, and for this reason the slide-valve would give an excessive amount of compression if it were made to cut off the supply of steam earlier than about half-stroke.

Fig. 35.—Diagram of Joy’s Valve-Gear.

Hence, where an early cut-off is wanted it is necessary either to use an entirely different means of regulating the distribution of steam, or to supplement the slide-valve by another valve—called an expansion-valve, usually driven by a separate eccentric—whose function is to effect the cut-off, the other events being determined as usual by the slide-valve.

Fig. 36.—Joy’s Gear as applied to a Locomotive.

Such expansion-valves belong generally to one or other of two types. In one the expansion-valve cuts off the supply of steam to the chest In which the main valve works.

Fig. 37.—Expansion-Valve on back of Main Slide-Valve.

In the other the expansion-valve slides on the back of the main
Fig. 38. slide-valve, which is provided with through ports which the expansion-valve opens and closes. Fig. 37 shows one form of this type. Here the resultant relative motion of the expansion-valve and main-valve has to be considered. If 𝑟_𝑎 and 𝑟 (fig. 38) are the eccentrics working the main and expansion valves respectively, then CR drawn equal and parallel to ME is the resultant eccentric which determines the motion of the expansion-valve relatively to the main-valve. Cut-off occurs at Q, when the shaft has turned through an angle φ, which brings the resultant eccentric into the direction CQ and makes the relative displacement of the two valves equal to the distance 𝑙.

Expansion-valves furnish a convenient means of varying the expansion, which may be done by altering their lap, travel or angular advance. Alteration of lap, or rather of the distance 𝑙 in the figures, is often effected by having the expansion-valve in two parts (as in fig. 37) and holding them on one rod by right- and left-handed screws respectively; by turning the valve-rod the parts are made to approach or recede from each other. In large valves the adjustment is more conveniently made by varying the travel of the valve, which is done by connecting it to its eccentric through a link which serves as a lever of variable length.

Fig. 39.

72. Relief Rings.—To relieve the pressure of the valve on the seat, large slide-valves are generally fitted with a steam-tight ring, which excludes steam from the greater part of the back of the valve. The ring fits steam-tight into a recess in the cover of the steam-chest, and is pressed by springs against the back of the valve, which is planed smooth to slide under the ring. Fig. 39 shows a relief ring of this kind fitted on the back of a large double-ported slide-valve for a marine engine. Another plan is to fit the ring into a recess on the back of the valve, and let it slide on the inside of the steam-chest cover. Steam is thus excluded from the space within the ring, any steam that leaks in being allowed to escape to the condenser (or to the intermediate receiver when the arrangement is fitted to the high-pressure cylinder of a compound engine). A flexible diaphragm has also been used, instead of a recess, to hold the ring.

73. Piston Slide-Valve.—The pressure of valves on cylinder faces is still more completely obviated by making the back of the valve similar to its face, and causing the back to slide in contact with the valve-chest cover, which has recesses corresponding to the cylinder ports. This arrangement is most perfectly carried out in the slide-valves now very largely used in the high-pressure cylinders of marine engines. The piston slide-valve may be described as a slide-valve in which the valve face is curved to form a complete cylinder, round whose whole circumference the ports extend. The pistons are packed like ordinary cylinder pistons by metallic rings, and the ports are crossed here and there by diagonal bars to keep the rings from springing out as the valve moves over them. Fig. 40 shows a form of piston valve for the supply of high-pressure steam to a large marine engine. P, P are the cylinder ports.

Fig. 40.—Piston
Slide-Valve.

74. Balance Piston.—Fig. 39 illustrates an arrangement common in all heavy slide-valves whose travel is vertical—the balance piston, which Is pressed up by steam on its lower side and so equilibrates the weight of the valve, valve-rod and connected parts of the mechanism.

The valve sometimes takes the form of a rocking cylinder. This last kind of sliding motion is very usual in stationary engines fitted with Corliss gear, in which case four distinct rocking slides are commonly employed to effect the steam distribution, one giving admission and one giving exhaust at each end of the cylinder.

75. Double-Beat Valve.—In many stationary engines, especially on the continent of Europe, lift or mushroom valves are used, worked by tappets, cams or eccentrics. Lift-valves are generally of the Cornish or double-beat type (fig. 41), in which equilibrium is secured by the use of two conical faces which open or close together. In Cornish pumping engines, which retain the single action of Watt’s early engine, three double-beat valves are used, as steam-valve, equilibrium-valve and exhaust-valve respectively. These are closed by tappets on a rod moving with the beam, but are opened by means of a device called a cataract, which acts as follows: The cataract is a small pump with a weighted plunger, discharging fluid through a stop-cock which can be adjusted by hand when it is desired to alter the speed of the engine. The weighted plunger is raised by a rod from the beam, but is free in its descent, so that it comes down at a rate depending on the extent to which the stop-cock is opened. When it comes down a certain way it opens the steam and exhaust valves, by liberating catches which hold them closed; the “out-door” stroke then begins and admission continues until the steam-valve is closed: this is done directly by the motion of the beam, which also, at a later point in the stroke, closes the exhaust. Then the equilibrium-valve is opened, and the “in-door” stroke takes place, during which the plunger of the cataract is raised. When it is completed, the piston pauses until the cataract causes the steam-valve to open and the next “out-door” stroke begins. By applying a cataract to the equilibrium-valve also, a pause is introduced at the end of the “out-door” stroke. Pauses have the advantage of giving the pump time to fill and of allowing the pump-valves to settle in their seats without shock.

Fig. 41.—Double-Beat Lift Valve.

76. Methods of Regulating.—To make an engine run steadily an almost continuous process of adjustment must go on, by which the amount of work done by the steam in the cylinder is adapted to the amount of external work demanded of the engine. Even in cases where the demand for work is sensibly uniform, fluctuations in boiler-pressure still make regulation necessary. Generally the process of government aims at regularity of speed; occasionally, however, it is some other condition of running that is maintained constant, as when an engine driving a dynamo-electric machine is governed by an electric regulator to give a constant difference of potential between the brushes.

The ordinary methods of regulating are either (𝑎) to alter the pressure at which steam is admitted by opening ot closing more or less a throttle-valve between the boiler and the engine, or (𝑏) to alter the volume of steam admitted to the cylinder by varying the point of cut-off. The former plan, was introduced by Watt and is still common, especially in small engines. The second plan of regulating is generally preferred, especially when the engine is subject to large variations of load. Within certain limits regulation by either plan can be effected by hand, but for the finer adjustment of speed some form of automatic governor is necessary. Speed governors are commonly of the centrifugal type: a pair of masses revolving about a spindle which is driven by the engine are kept from flying out by a certain controlling force. When an increase of speed occurs this controlling force is no longer able to keep the masses revolving in their former path; they move out until the controlling force is sufficiently increased, and in moving out they act on the regulator of the engine, which may be a throttle-valve or some form of automatic expansion gear. In the conical pendulum governor of Watt (fig. 42) the revolving masses are balls attached to a vertical spindle by links, and the controlling force is furnished by the weight of the balls, which, in receding from the spindle, are obliged to rise. When the speed exceeds or falls short of its normal value they move out or in, and so raise or lower a collar 𝑐 which is in connexion by a lever with the throttle-valve.


Fig. 42.—Watt’s Governor.		Fig. 43.—Loaded Governor.

77. Loaded Governor.—In a modified form, known as the loaded governor, a supplementary controlling force is given by placing a weight on the sliding collar (fig. 43). This is equivalent to increasing the weight of the balls without altering their mass. In other governors the controlling force is wholly or partly produced by springs. The use of springs to provide controlling force allows the axis of rotation to be horizontal, and governors of this class are frequently attached directly to the horizontal shaft in high-speed engines.

78. Equilibrium of Governor.—In whatever way the revolving masses are controlled, the controlling force may be treated as a force F acting on each ball in the direction of the radius towards the axis of revolution. Then, if M be the mass of the ball, 𝑛 the number of revolutions per second and 𝑟 the radius of the ball’s path, the governor will revolve in equilibrium when F＝4π²𝑛²𝑟M (in absolute units), or

𝑛＝1/2π√F/M𝑟.

In order that the configuration of the governor should be stable, F must increase more rapidly than 𝑟, as the balls move outwards. It is obvious that no stable governor maintains a strictly constant speed in the engine which it controls. If the boiler pressure or the demand for work is changed, a certain amount of permanent displacement of the balls is necessary to alter the steam-supply, and the balls can retain their displaced position only by virtue of a permanent change in the speed. The maximum range of speed depends on that amount of change of 𝑛 which suffices to alter the configuration of the governor from the position which gives no steam-supply to the position which gives full steam-supply, and the governor is said to be sensitive if this range is a small fraction of 𝑛.

To find the configuration which the governor will assume at any particular speed, or the speed corresponding to a particular configuration, it is only necessary to determine the whole controlling force F per ball acting along the radius towards the axis for various values of 𝑟. Let a curve 𝑎𝑏 (fig. 44) be drawn
Fig. 44. showing the relation of F to 𝑟. At any assigned value of 𝑟 set up an ordinate QC = 4π²𝑛²𝑟M. Join OC. The point 𝑐, in which OC cuts the curve, determines the value of 𝑟 at which the balls will revolve at the assigned speed 𝑛. Or, if that is given, and the value of 𝑛 is to be found, the line O𝑐 produced will determine C, and then 𝑛² = 4π²𝑛²𝑟M. The sensibility of the governor is determined by taking points 𝑎 and 𝑏 corresponding to full steam and no steam respectively, and drawing lines through them to determine the corresponding values of QA and QB. When the frictional resistance 𝑓 is known, an additional pair of curves drawn above and below ab, with ordinates F + 𝑓 and F − 𝑓 respectively, serve to show the additional variations in speed which are caused by friction. The governor is stable throughout its whole range when the curve 𝑎𝑏 has a steeper gradient than any line drawn from O to meet it.

79. Isochronism.—If, when the balls are displaced, the controlling force F changes proportionally to the radius 𝑟, the speed is constant. In other words, the equilibrium of the governor is then neutral; it can revolve in equilibrium at one, and only at one, speed. At this speed it assumes, indifferently, any one of its possible configurations. The slightest variation of speed drives it to the extremity of its range; hence its sensibility is indefinitely great. Such a governor is called isochronous. Where springs furnish the controlling force, an approach to isochronism can be secured by adjusting the initial tension of the springs, and this forms a convenient means of regulating the sensibility.

But in practice no governor can be absolutely isochronous. It is indispensable to leave a small margin of stability for the sake of preventing violent change in the supply of steam, especially when there is much frictional resistance to be overcome by the governor, or where the influence of the governor takes much time to be felt by the engine. An over-sensitive governor is liable to fall into a state of oscillation called hunting. When an alteration of speed begins to be felt, however readily the governor alters its form, the engine’s response is more or less delayed. If the governor acts by closing a throttle-valve, the engine has still a capacious valve-chest on which to draw for steam. If it acts by changing the cut-off, its opportunity is passed if the cut-off has already occurred, and the control only begins with the next stroke.

When the demand for power suddenly falls, the speed rises so much as to force the governor into a position of over-control, such that the supply of steam is no longer adequate to meet even the reduced demand for power. Then the speed slackens, and the same kind of excessive regulation is repeated in the opposite direction. A state of forced oscillation is consequently set up. The effect is aggravated by the momentum which the governor balls acquire in being displaced. Hunting is to be avoided by giving the governor a fair degree of stability, by reducing as far as possible the static frictional resistances, and by introducing a viscous resistance to the displacement of the governor, which prevents the displacement from occurring too suddenly, without affecting the ultimate position of equilibrium. For this purpose many governors are furnished with a dash-pot, which is a hydraulic or pneumatic brake, consisting of a piston connected to the governor, working loosely in a cylinder which is filled with oil or with air.

80. Regulation by the Governor of the Steam-Supply: Throttle-Valve.—The throttle-valve, as introduced by Watt, was originally a disk turning on a transverse axis across the centre of the steam-pipe. It is now usually a double-beat valve or a piston-valve. When regulation is effected by varying the cut-off, and an expansion-valve of the slide-valve type is used, the governor generally acts by changing the travel of the valve. In other forms of automatic expansion-gear the lap of the valve is altered; in others the governor acts by shifting the expansion-valve eccentric round on its shaft, and so changing its angular advance.

Fig. 45.—Corliss Engine, with Spencer Inglis Trip-Gear.

81. Trip-Gear.—In large stationary engines the most usual plan of automatically regulating the expansion is to employ some form of trip-gear, the earliest type of which was introduced in 1849 by G. H. Corliss (1817–1888), of Providence, U.S.A. In the Corliss system the valves which admit steam are distinct from the exhaust-valves. The latter are opened and closed by a reciprocating piece which takes its motion from an eccentric. The former are opened by a reciprocating piece, but are closed by springing back when released by a trip- or trigger-action. The trip occurs earlier or later in the piston’s stroke according to the position of the governor. The admission-valve is opened by the reciprocating piece with equal rapidity whether the cut-off is going to be early or late. It remains wide open during the admission, and then, when the trip-action comes into play, it closes suddenly. The indicator diagram of a Corliss engine consequently has a nearly horizontal admission-line and a sharply defined cut-off. Generally the valves of Corliss engines are cylindrical plates turning in hollow cylindrical seats which extend across the width of the cylinder. Often, however, the admission-valves in trip-gear engines are of the disk or double-beat type, and spring into their seats when the trip-gear acts. Messrs Sulzer have developed, this type with much success. Many forms of trip-gear have been invented by Corliss himself and by others. One of these, the Spencer Inglis trip-gear, by Messrs Hick, Hargreaves & Co., is shown in figs. 45 and 46. A wrist-plate A, which turns on a pin on the outside of the cylinder, receives a motion of oscillation from an eccentric. It opens the cylindrical rocking-valve B by pulling the link C, which consists of two parts, connected to each other by a pair of spring clips 𝑎, 𝑎. Between the clips there is a rocking-cam 𝑏, and as the link is pulled down this cam places itself more and more athwart the link, until at a certain point it forces the clips open. Then the upper part of the link springs back and allows the valve B to close by the action of a spring in the dash-pot D. When the wrist-plate makes its return stroke the clips re-engage the upper portion of the link C, and things are ready for the next stroke. The rocking-cam 𝑏 has its position controlled by the governor through the link E in such a way that when the speed of the engine increases it stands more athwart the link C, and therefore causes the clips to be released at an earlier point in the stroke. A precisely similar arrangement governs the admission of steam to the other end of the cylinder. The exhaust-valves are situated at the bottom of the cylinder, and receive an oscillating motion from a separate wrist-plate, behind A.

Fig. 46.—Corliss Valve-Gear, Spencer Inglis form.

82. Use of Flywheel.—Besides those variations of speed which occur from stroke to stroke, which it is the business of the governor to check, there are variations within each single stroke due to the varying rate at which work is done on the crank-shaft during its revolution. To limit these is the function of the flywheel, which acts by forming a reservoir of energy to be drawn upon during those parts of the revolution in which the work done on the shaft is less than the work done by the shaft, and to take up the surplus in those parts of the revolution in which the work done on the shaft is greater than the work done by it. This alternate storing and restoring of energy is accomplished by slight fluctuations of speed, whose range depends on the ratio which the alternate excess and defect of energy bears to the whole stock the flywheel holds in virtue of its motion. The effect of the flywheel may be studied by drawing a diagram of crank-effort, which shows the work done on the crank in the same way that the indicator diagram shows the work done on the piston. The same diagram serves another useful purpose in determining the twisting and bending stress in the crank.

The diagram of crank-effort is drawn by representing, in rectangular co-ordinates, the relation between the moment which the connecting-rod exerts to turn the crank and the angle turned through by the crank. The moment exerted to turn the crank is readily found when the direction and magnitude of the thrust exerted by the connecting-rod on the crank-pin is known for successive points in the revolution.

83. Influence of the Inertia of the Reciprocating Masses.—This thrust depends not only, on the resultant pressure of the steam on the piston but also on the inertia of the reciprocating masses. The mass of the piston, piston-rod, cross-head, and to some extent that of the connecting-rod also, has to be started and stopped in each half revolution, and in high-speed engines the forces concerned in this action are so large as to affect most materially not only the distribution of crank-effort but also the stresses which the various parts have to be proportioned to bear. The calculation of the stresses due to inertia in high-speed engines consequently forms an essential part of engine design. Taking M to represent the whole reciprocating mass, and 𝑎 its acceleration at any instant in the direction of the piston’s motion, the force required to produce this acceleration is M𝑎/𝑔, and this quantity has to be deducted from the resultant pressure of the steam in finding the effective thrust. The effect is to reduce the effective thrust at the beginning of the stroke and to increase it at the end. The greatest acceleration 𝑎 occurs in the extreme position of the piston, most distant from the crank-shaft centre, and its value there is 4π²𝑛²𝑟(1 + 𝑟/𝑙) where 𝑟 is the radius of the crank, 𝑙 the length of the connecting-rod and 𝑛 the number of turns per second. When the piston is in the other extreme position, nearest to the shaft, the value of 𝑎 is 4π²𝑛²𝑟(1 − 𝑟/𝑙). The exact calculation of inertia effects for the connecting-rod is complicated, but its influence on the thrust is approximately found by treating the mass of the rod as divided into two parts, one of which moves with the cross-head and is therefore an addition to the reciprocating system, while the other moves with the crank-pin and is therefore an addition to the revolving system. The mass may be divided for this purpose into parts which are inversely proportional to the distances of the centre of gravity from the cross-head and crank-pin respectively. By combining diagrams of the steam thrust and of the forces due to inertia a diagram is obtained showing the true thrust throughout the stroke. Fig. 47 gives an
Fig 47. example: there the line 𝑎𝑏 is drawn to show the inertia forces for an engine in which the connecting-rod has 31/2 times the length of the crank. The straight line 𝑐𝑑 shows what the inertia force would be if the connecting-rod were treated as being so long that the deviation from simple-harmonic motion might be neglected.

The inertia of the reciprocating parts imposes a limit on the lightness of engines of the piston and cylinder type. The proportion of weight to power is reduced by increasing mean piston speeds, but this process cannot be carried beyond a point at which the forces due to inertia become so great as to produce unsafely high alternating stresses in the piston-rods and other parts. In some torpedo-boat destroyers, where the reduction of weight has been carried as far as is practicable, the mean piston speed approaches 1200 ft. per minute with nearly 400 revolutions per minute and an 18-in. stroke. These engines develop 6000 h.p., and the weight of engines and boiler together is only 50 ℔ per indicated h.p. Such a figure is, however, to be regarded as exceptional; weights of 150 to 200 ℔ per h.p. are more usual even in conditions like those of high-speed cruisers where saving of weight is specially desirable.

84. Balancing.—Another aspect in which the inertia of the reciprocating parts is important is in regard to the balancing of the engine as a whole. Any forces required to accelerate the piston and its attached parts produce reaction on the frame and bed-plate of the engine, which will set up vibrational disturbances in the foundations and ground or the supporting structure. The object of balancing is to group the masses in such a manner that their inertia effects more or less neutralize one another. This is especially important in marine engines, where massive foundations are absent and where it may happen that the periodic impulses due to want of balance find some portion of the hull free to respond synchronously with vibrations so violent as to be inconvenient and even dangerous. Even in land engines a want of balance causes enough vibration to constitute a serious nuisance in the neighbourhood.

85. In considering the question of balance, the system of eccentrically revolving masses and the system of reciprocating masses have to be considered separately. A reciprocating mass such as a piston cannot be balanced by the use of revolving masses, for the forces which are due to the inertia of the piston necessarily act along the line of its stroke, while those due to revolving masses are continually changing their direction. The inertia of each connecting-rod may be approximately treated by resolving its mass into two constituents, one of which moves with the crank-pin, and is therefore an addition to the revolving system, while the other moves with the cross-head, and is therefore an addition to the reciprocating system. The mass of the rod may be divided for this purpose into parts which are inversely proportional to the distances of its centre of gravity from the crank-pin and the cross-head respectively. Let M₁, M₂, M₃, &c., represent the various revolving masses 𝑟₁, 𝑟₁, 𝑟₁, &c, their effective radii of rotation, and 𝑎₁, 𝑎₂, 𝑎₃, &c, their distances from any assumed plane of reference taken perpendicular to the shaft. Then the conditions necessary for balance amongst them are that the vector sum of M 𝑎 𝑟 shall vanish, and also that the vector sum of M 𝑟 shall vanish, this latter quantity being the resultant of the moments of the centrifugal forces with respect to the plane of reference. In a four-crank engine there is no serious difficulty in arranging the revolving masses in such a manner that these conditions shall be satisfied, so far as those masses are concerned. The problem, as Professor W. E. Dalby has shown, lends itself readily to graphical treatment (see his treatise on Balancing of Engines). With respect to the reciprocating masses, a first approximation towards balance is attained by satisfying the conditions which would secure balance if the motions were simply harmonic. These conditions are identical with those which have just been stated for the revolving masses, when 𝑟 is interpreted as the semi-amplitude of the harmonic motion. When the conditions in question are satisfied, the only remaining source of disturbance is that which comes from the fact that the reciprocating masses are connected to the cranks by rods of finite length; in other words, that the motions are not simply harmonic. For this reason the force required to accelerate each piston is greater when the piston is at the end of the stroke farthest from the shaft than when it is at the other end, and consequently the balance, which would be perfect if the connecting-rods were indefinitely long, is disturbed by the presence of forces which vary periodically with a frequency twice that of the rotation. When three cranks, 120° apart, are employed, it will be found that the effect of the shortness of the connecting-rods in causing forces to act in the line of the stroke is reduced to a couple tending to tilt the engine in a fore and aft direction, which may in its turn be balanced by using a second set of three cranks on the same shaft, the second set being so arranged that the couple to which it gives rise neutralizes the couple due to the first set. A six-crank engine may be arranged in this way to secure an extremely close approximation to perfect balance, and the same state of balance can be secured when the number of cranks is reduced to five.

86. The most usual arrangement adopted in marine engines, when questions of balance are taken into account, is to have four cranks, and consequently four sets of reciprocating masses. In the “Yarrow-Schlick-Tweedy” system of balancing engines four cranks are employed, and by adjusting the relative weights of the four pistons, as well as their distances apart, and by selecting suitable angles for the relative positions of the cranks (differing somewhat from 90°), a close approximation to complete balance is obtained. In triple expansion this arrangement is readily applied when two low-pressure cylinders are used instead of one, the steam from the intermediate cylinder being divided between them, and it is also of course applicable to quadruple expansion engines.

87. In this connexion mention may be made of a type of engine which has been used in various electric power stations, especially in America, in which a revolving mass might be employed to balance completely the inertia effects of two pistons. This is a compound engine in which the cylinders stand at right angles to one another, one being horizontal and the other vertical. If the piston masses were made equal it is clear that the inertia effect of a revolving mass could be resolved into two components which would balance both. It does not appear, however, that advantage has been taken of this property in the design of actual engines of this type. In the London County Council power station at Greenwich, where the engines are of this class, the unbalanced effects of inertia are so considerable as to affect the instruments at the Observatory half a mile away. One of the conspicuous merits of the steam turbine is that it avoids the use of reciprocating parts and so escapes the inconveniences and limitations to which the inertia of reciprocating parts gives rise.

88. Types of Engine.—In classifying engines with regard to their general arrangement of parts and mode of working, account has to be taken of a considerable number of independent characteristics. We have first a general division into condensing and non-condensing engines, with a subdivision of the condensing class into those which act by surface condensation and those which use injection. Next there is the division into compound and non-compound, with a further classification of the former as double-, triple- or quadruple-expansion engines. Again, engines may be classed as single or double-acting, according as the steam acts on one or alternately on both sides of the piston. Again, a few engines—such as steam hammers and certain kinds of steam pumps—are non-rotative, that is to say, the reciprocating motion of the piston does work simply on a reciprocating piece; but generally an engine does work on a continuously revolving shaft, and is termed rotative. In most cases the crank-pin of the revolving shaft is connected directly with the piston-rod by a connecting-rod, and the engine is then said to be direct-acting; in other cases, of which the ordinary beam engine is the most important example, a lever is interposed between the piston and the connecting-rod. The same distinction applies to non-rotative pumping engines, in some of which the piston acts directly on the pump-rod, while in others it acts through a beam. The position of the cylinder is another element of classification, giving horizontal, vertical and inclined cylinder engines. Many vertical engines are further distinguished as belonging to the inverted cylinder class; that is to say, the cylinder is above the connecting-rod and crank. In oscillating cylinder engines the connecting-rod is dispensed with; the piston-rod works on the crank-pin, and the cylinder oscillates on trunnions to allow the piston-rod to follow the crank-pin round its circular path. In trunk engines the piston rod is dispensed with; the connecting-rod extends as far as the piston, to which it is jointed, and a trunk or tubular extension of the piston, through the cylinder cover, gives room for the rod to oscillate. In rotary engines there is no piston in the ordinary sense; the steam does work on a revolving piece, and the necessity is thus avoided of afterwards converting reciprocating into rotary, motion. Steam turbines may, in one sense, be regarded as an extreme development of the rotary type; but they are distinct from all other steam engines in this that their action depends on the kinetic energy of the steam.

89. Beam Engines.—In the single-acting atmospheric engine of Newcomen the beam was a necessary feature; the use of water-packing for the piston required that the piston should move down in the working stroke, and a beam was needed to let the counterpoise pull the piston up. Watt’s improvements made the beam no longer necessary; and in one of the forms he designed it was discarded—namely, in the form of pumping engine known as the Bull engine, in which a vertical inverted cylinder stands over and acts directly on the pump-rod. But the beam type was generally retained by Watt, and for many years it remained a favourite with builders of engines of the larger class. The beam formed a convenient driver for pump-rods and valve-rods; and the parallel motion (q.v.) invented by Watt as a means of guiding the piston-rod, which could easily be applied to a beam engine, was, in the early days of engine-building, an easier thing to construct than the plane surfaces which are the natural guides of the piston-rod in a direct-acting engine. In modern practice the direct-acting type has to a very great extent displaced the beam type. For mill-driving and the general purposes of a rotative engine the beam type is now rarely chosen. In pumping engines it is somewhat more common, but even there the direct-acting forms are generally preferred.

90. Direct-Acting Engines.—Of direct-acting engines the horizontal type has in general the advantage of greater accessibility, but the vertical economizes floor space. In small forms the engine is generally self-contained, that is to say, a single frame or bedplate carries all the parts including the main bearings in which the crank-shaft with its flywheel turns. The frame often takes what is called a girder shape, which brings a portion of it into a favourable position for taking the thrust between the cylinder and the crank-shaft bearings and allows two surfaces to be formed on the frame to serve as guides for the cross-head. When a condenser is used with a horizontal engine it is usually placed behind the cylinder, and the air-pump, which is within the condenser, has a horizontal plunger or piston on a “tail-rod” or continuation of the main piston-rod through the back cover of the cylinder. In large horizontal engines the condenser generally stands in a well below, and its pump, which is vertical, is driven by means of a bell-crank lever attached by a link to the engine cross-head.

91. Coupled Engines.—When uniformity of driving effort or the absence of dead points is important, two independent cylinders often work on the same shaft by cranks at right angles to each other. Such engines, which are called “coupled,” can start readily from any position; the ordinary locomotive engine is an example. Winding engines for mines and collieries, in which ease of starting, stopping and reversing is essential, are very generally made by coupling a pair of cylinders on opposite sides of the winding drum with link motions as the means of operating the valves.

92. Compound Engines, Coupled or Tandem.—Large direct-acting engines are usually compounded either by having a high- and a low-pressure cylinder side by side, with cranks at right angles, or by putting one cylinder behind the other with the axes of both in the same line. The latter is called the tandem arrangement. In a tandem engine, since the pistons agree in phase, the steam may expand directly from the small into the large cylinder. But the connecting-pipe and steam chest form a receiver of considerable size, and to avoid loss by “drop” the supply of steam to the large cylinder is cut off long before the end of the stroke. For mill engines the compound tandem and compound coupled types of engine are the most usual. The high-pressure cylinder is very generally fitted with Corliss or other trip-gear.

93. Jet and Surface Condensation.—In land engines using condensation the jet form of condenser is common, but surface condensation is resorted to when the available water-supply is unsuited for boiler feed. When there is no large supply of condensing water a very fair vacuum can be obtained by using an evaporative condenser, consisting of a stack of pipes into which the exhaust steam is admitted and over which a small amount of cooling water is allowed to drip. This water is evaporated by the heat which is extracted in condensing the steam within. Such a condenser is placed in the open, generally on a roof where the air has free access. The amount of water it uses need not exceed the amount of steam that is condensed, and is therefore a very small fraction of the amount required in a jet or surface condenser.

94. High-Speed Direct-Acting Engines.—Prior to the advent of the steam turbine the demand for engines suitable for driving electric generators without the intervention of a belt led to the introduction of various forms of direct-acting engine adapted to run at a high speed. Some of these were single acting, steam being admitted to one side of the piston only, generally the back, with the result that the rods could be kept in a state of thrust throughout the revolution, and alternations of stress in them and at the joints thereby avoided, together with the knocking and wear of the bearing brasses which it is apt to cause. To secure, however, that the connecting-rod should always push and never pull against the crank-pin there had to be much cushioning during the out stroke on account of the fact that from about the middle of that stroke to the end the reciprocating mass was being retarded. In engines designed by P. W. Willans, which were highly successful examples of this class, the cushioning was provided by means of a supplementary piston which compressed air during the out stroke; the energy which the reciprocating masses had to part with in losing their motion during the second half of the out stroke was stored in this air and was restored in the succeeding down stroke.

Willans obtained compound or triple expansion by mounting two or three cylinders in tandem in a vertical line, with the air-compressing piston below them in the form of a trunk which served also as a guide for the cross-head. The piston-rod was hollow and within it there was a valve rod carrying piston valves for the admission and release of the steam. The valve rod was worked by an eccentric on the crank-pin which gave it the proper relative motion with respect to the hollow piston within which it works. The engine was entirely enclosed in a casing the bottom of which formed an oil bath in which the cranks splashed to ensure ample lubrication. These engines for a time had much vogue and gave good results. Many of them are in use in electric light stations and elsewhere, but the tendency now is to use turbines for this class of work, and even in cases where reciprocating engines are preferred they are now more usually of the double-acting type, which has the advantage of giving a greater output of power for the same weight.

95. Double-Acting High-Speed Engines.—Of double-acting high-speed engines an interesting form is that of Messrs Belliss and Morcom, the chief distinctive feature of which is the use of forced lubrication at the pin joints and shaft bearings. In a double-acting engine, where the thrust acts alternately on one and the other side of the crank-pins and cross-head pins, high frequency of stroke tends to produce much knocking and wear unless the brasses are very closely adjusted, and in that case the pins are liable to get hot, and to “seize” by expanding sufficiently to fill the small clearance. This difficulty, which exists when lubrication is carried out in the ordinary way, is overcome in the Belliss engine by feeding the bearings with a continuous supply of oil, which is pumped in under a pressure of about 15 ℔ per sq. in. The presence of a film of oil is thereby continuously secured, and knocking is prevented although the brasses are not set very close. Notable examples in which double action is combined with a relatively high frequency of stroke are found in naval engineering practice, especially in the engines of high-speed cruisers and torpedo-boat destroyers. As a rule these engines employ triple expansion with four cranks and four cylinders, the third stage of the expansion being performed in two cylinders, which divide the steam between them. But in this field also the steam turbine is rapidly displacing the reciprocating type.

96. Pumping Engines.—In engines for pumping or for blowing air it is not essential to drive a revolving shaft, and in many forms the reciprocating motion of the steam piston is applied directly or through a beam to produce the reciprocating motion of the pump-piston or plunger. On the other hand, pumping engines are frequently made rotative for the sake of adding a flywheel.

Fig. 48 shows a compound inverted vertical pumping engine of the non-rotative class by Messrs Hathorn, Davey & Co. Steam is distributed through lift valves, and the distribution of steam is controlled by means of a cataract, which makes the pistons pause at the end of each stroke. The pistons are in line with two pump-rods, and are coupled by an inverted beam which gives guidance to the cross-heads by means of an approximate straight-line motion.

Fig. 48.—Vertical Non-Rotative Pumping Engine.

Engines of this kind, like the old Cornish pump, are able to work expansively against a uniform resistance without a flywheel in consequence of the great inertia of the reciprocating pieces which include long massive pump-rods. Notwithstanding the low frequency of the strokes, enough energy is stored in the moving rods to counterbalance the inequalities of steam thrust, and the rate of acceleration of the system adjusts itself to give, at the plunger end, the nearly uniform effort which the pump requires. In other words, the motion, instead of being almost simple harmonic as it is in rotative engines, is such that the form of the inertia curve when drawn as in fig. 47 is nearly the same as that of the steam curve, with the result that the distance between the two, which represents the net effort on the pump-plunger, is nearly constant. The massive pump-rods act in such a way as to form a reciprocating equivalent of a flywheel.

97. It is, however, only to deep well pumping that this applies, and a very numerous class of direct-acting steam pumps have too little mass in their reciprocating parts to allow such an adjustment to take place. A familiar example is the small donkey pump used for feeding boilers, in which the steam-piston and pump-plunger are on one and the same rod. In some of these pumps a rotative element is introduced, partly to secure steadiness of working and partly for convenience in working the valves. But many pumps of this class are entirely non-rotative, and in such cases the steam is generally admitted throughout the stroke without expansion. In some of them the valve is worked by tappets from the piston-rod. In the Blake steam pump a tappet worked by the piston as it reaches each end of its stroke throws over an auxiliary steam-valve, which admits steam to one or other side of an auxiliary piston carrying the main slide-valve.

98. Worthington Engines.—In the Worthington pumping engine two steam cylinders are placed side by side, each working its own pump-piston. The piston-rod of each is connected by a short link to a swinging bar, which actuates the slide-valve of the other steam cylinder. In this way one piston begins its stroke when the motion of the other is about to cease, and a smooth and continuous action is secured. These engines have been extensively applied, on a large scale, to raise water for the supply of towns and to force oil through “pipe-lines” in the United States. In the larger sizes they are made compound, each high-pressure cylinder having a low-pressure cylinder tandem with it on the same rod. To allow of expansive working
Fig. 49. a device is added which compensates for the inequality of effort resulting from an early cut-off. A cross-head A (fig. 40) fixed to each of the piston-rods is connected to the piston-rods of a pair of oscillating cylinders B, B, which contain water and communicate with a reservoir full of air compressed to a pressure of about 300 ℔ per square inch. When the stroke (which takes place in the direction of the arrow) begins the pistons are at first forced in, and work is at first done by the main piston-rod, through the compensating cylinders B, B, on the compressed air in the reservoir. This continues until the cross-head has advanced so that the cylinders stand at right angles to the line of stroke. Then for the remainder of the stroke the compensating cylinders assist in driving the main piston, and the compressed air gives out the energy which it stored in the earlier portion. The volume of the air reservoir is so much greater than the volume of the cylinders, B, B, that the air pressure remains nearly constant throughout the stroke. Any leakage from the cylinder or reservoir is made good by a small pump which the engine drives.

99. Pulsometer.—Hall’s “pulsometer” is a peculiar pumping engine without cylinder or piston, which may be regarded as the modern representative of the engine of Savery. The sectional view, fig. 50, shows its principal parts. There are two chambers A, A′, narrowing towards the top, where the steam-pipe B enters. A ball-valve C allows steam to
Fig. 50. Pulsometer. pass into one of the chambers and closes the other. Steam entering (say) the right-hand chamber forces water out of it past the clack-valve V into a delivery passage D, which is connected with an air-vessel. When the water level in A sinks so far that steam begins to blow through the delivery passage, the water and steam are disturbed and so brought into intimate contact, the steam in A is condensed, and a partial vacuum is formed. This causes the ball-valve C to rock over and close the top of A, while water rises from the suction-pipe E to fill that chamber. At the same time steam begins to enter the other chamber A′, discharging water from it, and the same series of actions is repeated in either chamber alternately. While the water is being driven out there is comparatively little condensation of steam, partly because the shape of the vessel does not promote the formation of eddies, and partly because there is a cushion of air between the steam and the water. Near the top of each chamber is a small air-valve opening inwards, which allows a little air to enter each time a vacuum is formed. When any steam is condensed, the air mixed with it remains on the cold surface and forms a non-conducting layer. The pulsometer is, of course, far from efficient as a thermodynamic engine, but its suitability for situations where other steam-pumps cannot be used, and the extreme simplicity of its working parts, make it valuable in certain cases.

100. Rotary Engines.—From the earliest days of the rotative engine attempts have been made to avoid the intermittent reciprocating motion which an ordinary piston engine first produces and then converts into motion of rotation. Murdoch, the contemporary of Watt, proposed an engine consisting of a pair of spur-wheels gearing with one another in a chamber through which steam passed by being carried round the outer sides of the wheels in the spaces between successive teeth.

In Dudgeon’s wheel engine the steam was admitted by ports in side-plates into the clearance space behind teeth in gear with one another, just after they had passed the line of centres. From that point to the end of the arc of contact the clearance space increased in volume; and it was therefore possible, by stopping the admission of steam at an intermediate point, to work expansively. The difficulty of maintaining steam-tight connexion between the teeth and the side-plates on which the faces of the wheels slide is obvious; and the same difficulty has prevented the success of many other forms of rotary engine. These have been devised in immense variety, in many cases, it would seem, with the idea that a distinct mechanical advantage was to be secured by avoiding the reciprocating motion of a piston. In point of fact, however, very few forms entirely escape having pieces with reciprocating motion. In all rotary engines, with the exception of steam turbines—where work is done not by pressure but by the kinetic impulse of steam—there are steam chambers which alternately expand and contract in volume, and this action usually takes place through a more or less veiled reciprocation of working parts. So long as engines work at a moderate speed there is little advantage in avoiding reciprocation; the alternate starting and stopping of piston and piston-rod does not affect materially the frictional efficiency, throws no deleterious strain on the joints, and need not disturb the equilibrium of the machine as a whole. The case is different when very high speeds are concerned; it is then desirable as far as possible to limit the amount of reciprocating motion and to reduce the masses that partake in it.

101. Types of Marine Engines.—The early steamers were fitted with paddle-wheels, and the engines used to drive them were for the most part modified beam engines. Bell’s “Comet” was driven by a species of inverted beam engine, and another form of inverted beam, known as the side-lever engine, was for long a favourite with marine engineers. In the side-lever engine the cylinder was vertical, and the piston-rod projected through the top. From a crosshead on the rod a pair of links, one on each side of the cylinder, led down to the ends of a pair of horizontal beams or levers below, which oscillated about a fixed gudgeon at or near the middle of their length. The two levers were joined at their other ends by a cross-tail, from which a connecting-rod was taken to the crank above. The side-lever engine is now obsolete. In American practice, engines of the beam type, with a braced-beam supported on A frames above the deck, are still common in river-steamers and coasters. An old form of direct-acting paddle-engine was the steeple engine, in which the cylinder was set vertically below the crank. Two piston-rods projected through the top of the cylinder, one on each side of the shaft and of the crank. They were united by a crosshead sliding in vertical guides, and from this a return-connecting-rod led to the crank. Modern paddle-wheel engines are usually of one of the following types. (1) In oscillating cylinder engines the cylinders are set under the crank-shaft, and the piston-rods are directly connected to the cranks. The cylinders are supported on trunnions which give them the necessary freedom of oscillation to follow the movement of the crank. Steam is admitted through the trunnions to slide-valves on the sides of the cylinders. In some instances the mean position of the cylinders is inclined instead of vertical; and oscillating engines have been arranged with one cylinder before and another behind the shaft, both pistons working on one crank. The oscillating cylinder type is best adapted for what would now be considered comparatively low pressures of steam. (2) Diagonal engines are direct-acting engines of the ordinary connecting-rod type, with the cylinders fixed on an inclined bed and the guides sloping up towards the shaft.

When the screw-propeller began to take the place of paddle-wheels in ocean steamers, the increased speed which it required was at first supplied by using spur-wheel gearing in conjunction with one of the forms of engines then usual in paddle steamers. After a time types of engine better suited to the screw were introduced, and were driven fast enough to be connected directly to the screw-shaft. The smallness of the horizontal space on either side of the shaft formed an obstacle to the use of horizontal engines,: but this difficulty was overcome in several ways. In Penn’s trunk engine, now obsolete, the engine was shortened by attaching the connecting-rod directly to the piston, and using a hollow piston-rod, called a trunk, large enough to allow the connecting-rod to oscillate inside it. The return-connecting-rod engine was another horizontal form at one time used in the British navy. It was a steeple engine placed horizontally, with two, and in some cases four, piston-rods in each cylinder. The piston-rods passed clear of the shaft and the crank, and were joined beyond it in a guided crosshead, from which a connecting-rod returned.

102. Inverted Vertical Engines.—Both in the navy and in merchant ocean steamers one general type of engine is universal, where the reciprocating engine has not yet been displaced by the steam turbine. This is the inverted vertical direct-acting engine, with two or more cylinders placed side by side directly over the shaft. Two, three and four cranks are employed, the arrangement with four cranks being specially suitable, as has already been pointed out, when the balance of the engine at high speeds has to be secured. As a rule naval engines are triple compound, and those of merchant vessels either triple or quadruple. In vessels of high speed and power the engines are arranged in twin sets, on two shafts with twin screw propellers.

The marine engine is always furnished with a surface condenser, consisting of a multitude of brass tubes about 3/4 in. in diameter cooled by sea-water which is caused to circulate through the condenser by means of a circulating pump. This pump and also the air pump are often driven independently of the main engine.

103. It is in marine practice that the largest examples of engines are to be found. The triple expansion engines of the “Campania” and “Lucania,” which develop 30,000 h.p., consist of twin sets, on two shafts, each set having three cranks and five cylinders, two of 37 in., one of 70 in. and two of 98 in. diameter, with a stroke of 69 in. In the “Kaiser Wilhelm der Grosse” engines of the same power are arranged in twin sets, each set consisting of four cylinders, one of 52 in. diameter, one of 89 and two of 96·4, the four giving triple expansion and working on four cranks. The “Deutschland” develops 36,000 h.p. with twin sets, each of which comprises two 36·6-in. cylinders, one 73·6-in., one 103·9-in. and two 106·3-in. with a stroke of 72·8 in. In the “Kaiser Wilhelm II.” each of the twin shafts is driven by two 3-crank 4-cylinder quadruple expansion engines, the diameters being 37·4, 49·2, 74·8 and 112·2 in. and a stroke of 70·9 in. With a working pressure of 225 ℔ per square inch these engines develop in all 40,000 h.p. These are examples of the most powerful reciprocating engines used in the propulsion of ships, but the successful application of the Parsons turbine to marine use has enabled even these powers to be greatly surpassed.

104. Locomotive Engines.—The ordinary locomotive consists of a pair of direct-acting horizontal or nearly horizontal engines, fixed in a rigid frame under the front end of the boiler, and coupled to the same shaft by cranks at right angles, each with a single slide-valve worked by a link-motion, or by a form of radial gear. The engine is non-condensing, except in a very few special cases, and the exhaust steam, delivered at the base of the funnel through a blast-pipe, serves to produce a draught of air through the furnace. In some instances a portion of the exhaust steam, amounting to about one-fifth of the whole, is diverted to heat the feed-water. In tank engines the feed-water is carried in tanks on the engine itself; in other engines it is carried behind in a tender.

On the shaft are a pair of driving-wheels, whose frictional adhesion to the rails furnishes the necessary tractive force. In some engines a single pair of driving-wheels are used; in many more a greater tractive force is secured by having two equal driving-wheels on each side, connected by a coupling-rod between pins on the outside of the wheels. In some engines a still greater proportion of the whole weight is utilized to give tractive force by coupling three or more wheels on each side.

It is now general to have under the front of the engine two or four smaller wheels which do not form part of the driving system. These are carried in a bogie, that is, a small truck upon which the front end of the boiler rests by a swivel-pin or plate which allows the bogie to turn, so as to adapt itself to curves in the line, and thus obviate the grinding of tyres and danger of derailment which would be caused by using a long rigid wheel base. The bogie appears to have been of English origin;^[8] it was brought into general use in America, and is now common in English as well as in American practice. Instead of a four-wheeled bogie, a single pair of leading wheels are also used, carried by a Bissel pony truck, which has a swing-bolster pivoted by a radius bar about a point some distance behind the axis of the wheels. This has the advantage of combining lateral with radial movement of the wheels, both being required if the wheel base is to be properly accommodated to the curve. Another method of getting lateral and radial freedom is the plan used by F. W. Webb of carrying the leading axle in a box curved to the arc of a circle, and free to slide laterally for a short distance, under the control of springs, in curved guides.^[9]

In inside-cylinder engines the cylinders are placed side by side within the frame of the engine, and their connecting-rods work on cranks in the driving shaft. In outside-cylinder engines the cylinders are spread apart far enough to lie outside the frame of the engine, and to work on crank-pins on the outsides of the driving wheels. This dispenses with the cranked axle, which is the weakest part of a locomotive engine. Owing to the frequent alternation of strain to which it is subject, a locomotive crank axle is peculiarly liable to rupture, and has to be removed after a certain amount of use.

The outside-cylinder type is adopted by several British makers; in America it is almost universal.
Fig. 51.—American Outside-Cylinder Locomotive. There the cylinders are in castings which are bolted together to form a saddle on which the bottom of the smoke-box sits. The slide-valves are on the tops of the cylinders, and are worked through rocking levers from an ordinary link-motion. Fig. 51, which is a half section through one cylinder of an American locomotive, by the Baldwin Company of Philadelphia, shows the position of the cylinders and valves.

In inside-cylinder engines the slide-valves are frequently placed back to back in a single valve-chest between the cylinders. The width of the engine within the frame leaves little room for them there, and they are reduced to the flattest possible form, in some cases with split ports, half above and half below a partition in a central horizontal plane. In some engines the valves are below the cylinders: in many others the valves work on horizontal planes above the cylinders; this position is specially suitable when some form of radial gear is used instead of the link-motion. Radial valve-gears have the advantage, which is of considerable moment in inside-cylinder engines, that a part of the shaft’s length which would otherwise be needed for eccentrics is available to increase the width of main bearings and crank-pins, and to strengthen the crank-cheeks.

The principle of compounding has often been applied to locomotive engines, but without much advantage. On this subject the reader should refer to the article Railway: § Locomotive Power. A more important modern departure is the use of highly superheated steam, which in many locomotives has been attended with conspicuous success.

105. Steam Turbines.—Steam turbines are distinguished from all other types of steam engine by the fact that their action involves a double transformation of energy. The heat energy present in the steam is first employed to set the steam itself in motion, giving it kinetic energy, and this in turn is employed to do work on the turbine blades. A brief account of the main principles involved will make the action of the various types of steam turbine more intelligible.

106. Theory of the Steam-jet.—Consider an element of steam, of unit mass, acquiring kinetic energy in the expansion of the steam through a nozzle or other channel, from a region of pressure 𝑝₁ to a region of lower pressure 𝑝₂ . Its volume changes from 𝑣₁ to 𝑣₂ in the process. The work done upon it by steam from behind is 𝑝₁𝑣₁. The work which it does on the steam in front is 𝑝₂𝑣₂. The net amount of work done upon it is therefore 𝑝₁𝑣₁−𝑝₂𝑣₂. Its velocity changes from V₁ to V₂; the kinetic energy which it gains is therefore (V₂²−V₁²)/2𝑔. The internal energy changes from E₁ to E₂. Hence by the conservation of energy

(V₂²−V₁²)/2𝑔＝J(E₁−E₂)+𝑝₁𝑣₁−𝑝₂𝑣₂

which may be written

(V₂²−V₁²)/2𝑔＝J(I₁−I₂),

where I is the total heat (§ 31), which is equal to E+𝑝𝑣/J. It is assumed here that the action is adiabatic in the sense that no heat is received by the steam or given up by it to other bodies as the process goes on.

It is usual to speak of the change of I as the “heat drop” which the steam undergoes in acquiring velocity. When the heat drop is known the gain in velocity is readily found, as above. In determining the best drop account must, of course, be taken of the wetness of the steam, or of its superheat if it has any. Thus, for superheated steam I＝I_𝑠+κ(𝑡′−𝑡) where I_𝑠 is the total heat of saturated steam at the same pressure and κ(𝑡′−𝑡) represents the heat taken up in the process of superheating to the actual temperature 𝑡′ from the temperature of saturation 𝑡. And for wet steam I＝I_𝑤+𝑞L where I_𝑤 is the total heat of water, L the latent heat, and 𝑞 is the dryness fraction.

During this process of expansion, which we assume to be adiabatic, the steam becomes wet, and the value of 𝑞 accordingly falls. As has been shown in § 36, the dryness may be found at any stage in adiabatic expansion from the formula—

𝑞＝τ/L(𝑞₁L₁/τ₁+log ετ₁/τ),

or it may be determined by measurement from the entropy-temperature diagram. A still more convenient diagram in which the heat drop can be directly measured is one introduced by Mollier, in which the co-ordinates are the entropy and the total heat (see Mollier, loc. cit., or Ewing’s Steam Engine).

The pressure-volume diagram gives a very useful alternative means of finding the heat drop
Fig. 52 or energy available for transformation. Consider steam or any other gas supplied at pressure 𝑝₁ and expanding to pressure 𝑝₂, at which pressure it is discharged. The work which it does is measured by the area ABCD of the pressure-volume diagram (fig. 52), namely,

$\int _{p_{1}}^{p_{2}}vdp$ .

If this work is wholly done upon this steam in giving it velocity, the kinetic energy acquired is equal to it, that is

V₂²−V₁²/2𝑔＝ $\int _{p_{1}}^{p_{2}}vdp$ .

We have already seen (§ 41) that in adiabatic expansion this integral measures the heat drop, being equal to I₁−I₂.

If the mode of expansion is such as to make 𝑝𝑣^𝑛＝constant, 𝑛 being any index, then

$\int _{p_{1}}^{p_{2}}vdp$	＝𝑛/𝑛−1(𝑝₁𝑣₁ − 𝑝₂𝑣₂)
	＝𝑛/𝑛−1(1 − D^{𝑛−1/𝑛})𝑝₁𝑣₁,

where D is the ratio in which the pressure falls, namely 𝑝₂/𝑝₁.

Now the adiabatic expansion of steam, starting from an initially dry saturated state, is very approximately represented by the formula 𝑝𝑣^1·135＝constant. Hence the area of the pressure-volume diagram, which under these conditions measures the work theoretically obtainable, is equal to 8·41(1—D^0·119)𝑝₁𝑣₁, a quantity which will be found on evaluation to agree closely with the value of I₁−I₂.

107. Form of the Jet in Adiabatic Expansion.—As expansion proceeds the volume of the steam, per pound, at any stage is found by multiplying the volume of 1 ℔ of saturated steam, at the pressure then reached, by the dryness fraction 𝑞. On comparing the velocity acquired at any intermediate stage of expansion—as calculated from the heat drop down to that stage—with the increase in volume, it will be found that in the earliest stages the gain in velocity is relatively great, but as expansion proceeds the increase in volume outstrips the increase in velocity. Hence the proper form for a nozzle to give adiabatic expansion is one in which the area of section at first contracts and afterwards becomes enlarged. The area of section to be provided for the discharge is found by dividing the volume 𝑣 at each stage of the velocity V acquired up to that stage, and the ratio 𝑣/V at first diminishes and afterwards increases as the expansion proceeds. Take, for instance, as a numerical example, a case in which dry saturated steam is admitted to a nozzle at an absolute pressure of 213 ℔ per sq. in., and expands adiabatically, giving itself velocity, until the, pressure falls to 1·7 per sq. in. It will be found on working out numerical values that until the pressure falls to about 123 ℔ per sq. in. the steam is gaining velocity so rapidly that though its volume is expanding the stream-lines are convergent. Below that pressure, however, the augmentation of volume is relatively so great that a larger and larger area of section has to be provided for the flow. Thus, when the pressure is 123 ℔ per sq. in. the dryness 𝑞 is 0·96, the volume per pound is 3·51 cub. ft., the heat drop is 251/4 thermal units, giving a velocity of 1510 ft. per second. Consequently, the area of the stream is 0·00233 sq. ft. per pound of flow, and this is the minimum value. When the pressure falls to 1·7 ℔ per sq. in. the dryness 𝑞 is 0·784, the volume per pound is 157·8 cub. ft., the heat drop is 175·7 thermal units, giving a velocity of 3980 ft. per second, and consequently the area of the stream is 0·0396 sq. ft. per pound of flow.

108. De Laval’s Divergent Nozzle.—It is on this basis that De Laval’s divergent nozzle is designed. The “throat” or smallest
Fig. 53 section is approached by a more or less rounded entrance, allowing the stream-lines to converge, and from the throat outwards the nozzle expands in any gradual manner, generally in fact as a simple cone (fig. 53). In the example just given the final area of section would be seventeen times that of the throat to provide for adiabatic expansion down to a pressure of 1·7 ℔ per sq. in. With any final area less than this the pressure at exit would be higher than 1·7 ℔; it would in fact adjust itself to give a value of 𝑣/V corresponding to the area, and the remainder of the pressure drop would be wasted. For expansion to atmospheric pressure (14·7 per sq. in.) the area at exit would be 3·14 times that of the throat.

The equation of velocity

V²/2𝑔 ＝𝑛/𝑛−1 (1 − D𝑛−1/𝑛)𝑝₁𝑣₁

may be applied to calculate generally the discharge per square foot of stream section, and hence to find at what point in the fall of pressure this discharge becomes a maximum—in other words, to determine the pressure at the throat. Since 𝑝𝑣^𝑛＝𝑝₁𝑣₁^𝑛

𝑣＝𝑣₁/D^1/𝑛 where D＝𝑝/𝑝₁.

The discharge per square foot when the volume is 𝑣 is

Q＝V/𝑣＝VD^1/𝑛/𝑣₁＝√ {2𝑔𝑛/𝑛 − 1 · 𝑝₁/𝑣₁ ( D^2/𝑛 − D^𝑛+1/𝑛) } .

Q will be a maximum when 𝑑Q/𝑑D is zero, which occurs when

D＝(2/𝑛 + 1 )^{𝑛/𝑛−1}.

This result is general for any gas. With saturated steam, 𝑛 being 1·135, Q is a maximum when D＝0·577, that is to say, the pressure at the throat is 57·7% of the initial pressure, a result which agrees with the figures quoted above for a particular case.

The maximum value of Q, namely the discharge in pounds per square foot at the throat, is

3·6√(𝑝₁/𝑣₁),

and the velocity there is 5·85√(𝑝₁𝑣₁). In these expressions 𝑝₁ is the initial pressure in pounds per square foot.

109. From these considerations it follows that, provided the final pressure is less than 0·577 times the initial pressure, the total discharge depends simply on the least area of section of the nozzle and on the initial pressure, and is independent of the final pressure. By continuing the expansion in a divergent nozzle, after the throat is passed, the amount of discharge is not increased, but the steam is caused to acquire a greater velocity of exit, namely the velocity corresponding to the augmented pressure range.

110. When the pressure drop is small (𝑝₂ greater than 0·577 𝑝₁) the full velocity due to the drop is obtained without the use of a divergent nozzle. This is the case, for instance, in the Parsons turbine, where the whole expansion is divided into many stages each of which involves only a small drop in pressure.

111. Influence of Friction.—We have dealt so far with the ideal case of no friction, and have taken the whole work of expansion as going to produce kinetic energy in the jet. But under real conditions there is a progressive dissipation of energy through friction; as expansion proceeds the steam loses part of its kinetic energy which is restored to it as heat. Thus, at every stage in the process the velocity acquired is less than it would be in frictionless adiabatic expansion, but the steam is drier and its volume is greater in consequence of the restored heat. Referring to the entropy-temperature diagram
Fig. 54. (fig. 54) the process of expansion under conditions involving friction is represented not by the adiabatic line 𝑐𝑑 but by some such line as 𝑐𝑔 lying between the adiabatic line and the saturation line 𝑐𝑓. The final condition of dryness is 𝑎𝑔/𝑎𝑓 instead of 𝑎𝑑/𝑎𝑓. During this expansion the effect of friction, as regards the entropy, is equivalent to the communication to the substance of a quantity of heat represented by the area 𝑝𝑐𝑔𝑟. Hence that area represents the work converted by friction into heat. The whole work done during expansion is the area 𝑎𝑏𝑐𝑔, which is more than before by the area 𝑑𝑐𝑔. The difference, namely 𝑎𝑏𝑐𝑔 minus 𝑝𝑐𝑔𝑟, represents what may be called the net heat drop when friction is allowed for: it represents what is effectively available for giving kinetic energy to the jet. This net area may also be expressed as equal to 𝑎𝑏𝑐𝑑 minus 𝑝𝑑𝑔𝑟. Compared with frictionless adiabatic expansion the net loss resulting from friction is the area 𝑝𝑑𝑔𝑟. The volume is increased in the ratio of 𝑎𝑔 to 𝑎𝑑, and this has to be taken account of in determining the proper dimensions of the divergent nozzle.

112. Turning now to the question of utilizing the kinetic energy of steam in a steam turbine, it will be clear from the figures that have been given that if the whole heat drop is allowed to give kinetic energy to the steam in one operation, as in the De Laval nozzle, a velocity of about 4000 ft. per second has to be dealt with. To take advantage of a jet in the most efficient manner in a turbine consisting of a single wheel the velocity of the buckets against which the steam impinges should be nearly one half the velocity of the stream. But a peripheral velocity approaching 2000 ft. per second is impracticable. Apart from the difficulties which it would involve as regards gearing down to such a speed as would serve for the driving of other machines, which are to employ the power, there are no materials of construction fitted to withstand the forces caused by rotation at such a speed.

Hence it is advantageous to divide the process into stages. This may be done by using more than one wheel to absorb the kinetic energy of the jet, as is done in the Curtis turbine, or by dividing the heat drop into many steps, making each of these so small that the steam never acquires an inconveniently great velocity, as is done in the Parsons turbine. Turbines which employ one or other of these two methods, or a combination of both, achieve a greater economy of steam than is practicable with a single wheel.

113. De Laval Turbine.—Thanks, however, to the inventions of De Laval, the single expansion single wheel type of turbine, with buckets in the rim, has been brought to a degree of efficiency which, while considerably less than is reached in compound turbines, is still remarkably good. This has been done by the use of the divergent nozzle and with the help of mechanical devices which enable the peripheral speed to be very high, though even with the help of these devices the speed of the buckets falls considerably short of that which would be suitable to the velocity of the jet. In De Laval’s turbine the steam expands at one step from the full pressure of the supply to the pressure of the exhaust by discharge in the form of a jet from a divergent nozzle. It then acts on a ring of buckets or blades in much the same way as the jet of water acts on the buckets of a Pelton wheel or other form of pure impulse turbine. To utilize a fair fraction of the kinetic energy of the jet the blades have to run at an enormous velocity, and the speed of the shaft which carries them is so great that gearing down is resorted to before the motion is applied to useful purposes. The general arrangement of the steam nozzle and turbine blades is illustrated in fig. 55. The blades project from the circumference of a disk-shaped wheel and
Fig. 55. form a complete ring round it, only a few of the blades being shown in the sketch. The increasing section of the nozzle is calculated with reference to the final pressure, according to the principles already explained. The jet impinges at one side of the wheel and escapes at the other after having had its direction of motion nearly reversed. The expansion in the nozzle is carried to atmospheric pressure, or near it, if the turbine is to be used without a condenser; but in many cases an ejector condenser is employed, and when that is done the nozzle is of a form which adapts it to expand the steam to a correspondingly lower pressure. It is only in the smaller sizes of these turbines that a single nozzle is used; in the larger steam turbines, as in large Pelton wheels, several nozzles are applied at intervals along the circumference of the disk. The peripheral velocity of the blades ranges from about 500 ft. per second in the smallest sizes (5 h.p.) up to nearly 1400 ft. per second in turbines of 300 h.p. In a 50 h.p. De Laval turbine the shaft which carries the turbine disk makes 16,000 revolutions per minute; in the 5 h.p. size it makes as many as 30,000 revolutions per minute. A turbine developing 300 h.p. uses a wheel 30 in. in diameter, running at over 10,000 revolutions per minute, with a peripheral speed of nearly 1400 ft. per second. These enormous speeds are made possible by the ingenious device of using a flexible shaft, which protects the bearings and foundations from the vibration which any want of balance would otherwise produce. The elasticity of the shaft is such that its period of transverse vibration is much longer than the time taken to complete a revolution. The high-speed shaft which carries the turbine disk is geared, by means of double helical wheels with teeth of specially fine pitch, to a second-motion shaft, which runs at one-tenth of the speed of the first; and from this the motion is taken, by direct coupling or otherwise, to the machine which the turbine is to drive. The wheel carrying the buckets is much thickened towards the axis to adapt it to withstand the high stresses arising from its rotation. Turbines of this class in sizes up to 300 or 400 h.p. are now in extensive use for driving dynamos, fans and centrifugal pumps. Compared with the Parsons turbine, De Laval’s lends itself well to work where small amounts of power are wanted, and there
Fig. 56. it achieves a higher efficiency, but in large sizes the Parsons turbine is much the more efficient of the two. Trials of a De Laval turbine used with a condenser, and developing about 63 h.p., have shown an average steam consumption at the rate of about 20 ℔ per brake-horse-power-hour, and even better results are reported in turbines of a larger size.

114. Action of the Jet in De Laval’s Turbine.—In entering the turbine the jet is inclined at an angle a to the plane of the wheel. Calling its initial velocity V₁ and the velocity of the buckets 𝑢 we have, as in fig. 56, V₂ for the velocity of the steam relatively to the wheel on admission. A line AB parallel to V₂ therefore determines the proper angle of the blade or bucket on the entrance side if the steam is to enter without shock. As the steam passes through the blade channel the magnitude of this relative velocity does not change, except that it is a little reduced on account of friction. The action is one of pure impulse; there is no change of pressure during the passage, and consequently no acceleration of the steam through drop in pressure after once it has left the nozzle. Hence V₃, the relative velocity at exit may (neglecting friction) be taken as equal to V₂ The direction of V₃ or BC is tangent to the exit side of the bucket. Compounding V₃ with 𝑢 we find V₄, which is the absolute velocity of the steam after exit, and this should be no greater than is required to get the steam clear of the wheel. The most favourable condition of running would be when the bucket velocity 𝑢 is such that V₄ is perpendicular to the plane of the wheel, for V₄ would then have its least possible value. Assuming the angle of discharge β′ to be equal to β, we should in that event have 𝑢＝1/2V₁cos α, which approximates more and more closely to 1/2V₁ the smaller α is made. The ideal efficiency would be (V₁²−V₄²)/V₁² or 1−sin²α in a turbine in which the jet enters the buckets Without shock and travels over them without friction. In practice α is about 20°. Owing to the impossibility of making the bucket speed so high as the above condition implies the steam enters the buckets of a De Laval turbine with some shock and leaves them with a velocity inclined to the plane of the wheel, with a backward component, and the turbine loses something in efficiency through this exit velocity being greater than the ideal minimum.

Taking a test of a De Laval turbine of 300 h.p. in which the steam consumed was 15·6 lb per horse-power-hour, Stodola estimates that the losses in the nozzle amount to about 15% of the available energy or total heat drop, the losses in the buckets (due to friction and to eddy currents set up by shock) to 21% and the losses due to the velocity retained by the steam at exit to nearly 5%. The losses due to friction in the mechanism consume about 5% more, leaving a net return of about 54% of the available energy.

115. Curtis Turbine.—The Curtis turbine, like that of De Laval, is a pure impulse turbine, but the velocity of the jet is extracted not by one ring of buckets but by a series of rings, each of which extracts a certain part. Between the first and second rings of buckets there are fixed guide blades which serve to turn the remaining motion of the steam into a direction proper for its action on the second ring, and so on. The jet, having acquired its velocity in a nozzle in the first place, often acts on three successive rings of moving buckets, with two sets of fixed guide blades between, the three co-operating to extract its kinetic energy. But the Curtis turbine is generally compound in the further sense that the total drop from admission to condenser pressure is itself divided into two, three or more stages, the steam acquiring velocity anew at each stage and then giving up that velocity in passing through a series of impulse turbine rings generally either two or three in number before undergoing the next drop in pressure.

116. Action of the Steam in the Curtis Turbine.—In this division of the heat drop or pressure drop into stages Curtis follows Parsons. The distinctive feature in Curtis is the multi-impulse action which occurs at each pressure stage. This is illustrated in the diagram (fig. 57), which shows the nozzle and blades of a two-stage Curtis turbine, with three rings of moving blades or buckets in each stage, arranged, of course, round the periphery of a wheel.

Fig. 57.—Diagram of Steam Nozzles and Blades, Curtis Steam Turbine.

The velocity acquired in the nozzles is extracted as the steam pursues its sinuous course between moving and fixed blades, and it leaves the third ring in each case with only a small residual velocity, the direction of which is approximately parallel to the axis of the wheel. The changes of velocity are illustrated in fig. 58, which, for the sake of simplification, is drawn for the ideal case of no friction. There 𝑢 is the velocity of the buckets, V₁ the initial velocity of the jet, and the initial relative velocity on entrance to the first moving ring. V₃ is the absolute velocity on entering the second moving ring, and V₄ the relative velocity. V₅ is the absolute velocity on entering the third moving ring and V₆ the relative velocity. Finally, V₇ is the absolute velocity on leaving the third moving ring, and this in the example here drawn is parallel to the axis of the turbine. The first moving blades have sides parallel to OB, BP; the first fixed blades have sides parallel to CP, PD. The second moving blades have sides parallel to PE, EQ; the second fixed blades to FQ, QG, and the third moving blades to QH, HR.

Fig. 58.

The steam then passes on to a second set of divergent nozzles in which it undergoes a second drop in pressure, acquiring velocity afresh, which it loses as before in passing through a set of three rings of moving buckets. In some Curtis turbines this is followed by a third and often a fourth similar process before the condenser is reached. In a four-stage Curtis turbine the speed of the buckets is usually about 400 ft. per second; the steam issues from each set of nozzles with a velocity of about 2000 ft. per second, and each set of moving rings reduces this by something like 400 ft. per second. The losses due to steam friction are somewhat serious, although the blade speed in each set is sufficient to let the steam enter without shock; on the other hand, the Curtis turbine escapes to a great extent losses due to leakage which are present in the Parsons type. The velocity diagram shown in fig. 58 may readily be modified to allow for effects of friction. Owing to the progressive reduction of velocity in passing from ring to ring a larger and larger area of blade opening is required, and this is provided for by making the height of the blades increase in the successive rings of each series.

117. Performance of Curtis Turbines.—Curtis turbines have been successfully applied in large sizes, especially in America, to drive electric generators, with outputs of as much as 9000 kilowatts, and in a few instances they have been adapted to marine propulsion. In large sizes, and using moderately superheated steam, the Curtis turbine has achieved a high degree of efficiency. The advantage of superheating, in any type of turbine, is to reduce the wetness which the steam develops as it expands during work. The prejudicial effect of wetness is chiefly that it increases friction, especially in the later stages of the expansion. Tests of Curtis turbines show that they maintain a very uniform efficiency throughout a wide range of loads, and are capable of being much overloaded without

material increase in the ratio of steam consumption to output. In tests of a 9000 kilowatt Curtis turbine using steam of about 200 ℔ pressure and 80° C. superheat, with a vacuum of 295 in. the consumption of steam is reported to have been only 13 ℔ per kilowatt-hour, and this figure remained almost constant for loads ranging from 8000 to 12,000 kilowatts. In a 5000 kilowatt turbine under very similar conditions the consumption is reported to have been 135 ℔ per kilowatt-hour. In the usual arrangement of the Curtis turbine the shaft is vertical and the wheels lie in horizontal planes, the weight of the revolving parts being taken by a footstep bearing with forced lubrication, and the electric generator is mounted on the top. There are usually in the large sizes four stages of expansion, each stage being separated from the one above it by a diaphragm plate containing the nozzles in which the next step in velocity is acquired. The expansion has been divided into as many as seven stages in a Curtis turbine for marine use, the shaft being then horizontal, and in all except the first stage in that example the pressure drop is so comparatively small as not to require divergent nozzles.

118. Parsons Turbines.—In the turbines of De Laval and Curtis the action on the moving blades or buckets is entirely one of impulse. No drop of pressure occurs while the steam is passing the moving blades, and its velocity relative to the blade surface undergoes no change except such as is brought about by friction.

Fig. 59.—Fixed and Moving Blades
of Parsons Turbine.

In the Parsons turbine, on the other hand, there is a reaction effect. The steam acquires relative velocity and loses pressure as it passes each ring of moving blades: in this respect the action in the moving blades is like the action in the fixed blades. Each pair of fixed and moving rings makes up what is called a “stage” and may be said to constitute a separate turbine: the whole is a series of many such stages. In each stage the drop in pressure and in heat is divided equally between the fixed and moving element, the exit and entrance angles and the form of the blades generally being alike in both. The number of stages depends on what peripheral speed it is convenient to use. Where comparatively high blade speeds are practicable, as in turbines for driving electric generators, the steam is allowed to acquire a fairly high velocity at each ring of blades, and in such cases so few as 45 stages may be suitable. In large marine turbines, on the other hand, where the number of revolutions per minute has to be kept low in the interests of propeller efficiency, the blade speeds cannot be kept high without making the diameters unduly great, and consequently more stages are required: in such turbines the number of stages may be from 100 to 200. The general relation of fixed to moving blades and the characteristic form of both will be seen from fig. 59.

Fig. 60 shows a complete Parsons turbine of 1000 kilowatts capacity in longitudinal section through the casing. The fixed blades are caulked with separating distance-pieces into grooves turned on the inner surface of the case and project inwards: the moving blades are similarly secured in grooves which are turned on the surface of the rotating drum. Between drum and case there is an annular space fitted in this way with successive rings of fixed and moving blades. There is considerable longitudinal clearance from ring to ring, but over the tips of the blades the clearance is reduced to the smallest possible amount consistent with safety against contact (generally from 15 to 30 thousandths of an inch in turbines of moderate size). Steam enters at A, expands through all the rings of blades in turn and escapes to the condenser at B. To provide for the increase in its volume the size of the blade passages enlarges progressively from the high to the low pressure end. In the example shown this is done partly by lengthening the blades and partly by increasing the circumference of the drum, which has the further effect of increasing the blade velocity, so that the expanded steam not only has a larger area of passage open to it but is also allowed to move faster, and consequently each unit of the area is more effective in giving it vent. Instead of attempting to make the change in passage area continuous from ring to ring, as the ideal turbine would require, it is done in a limited number of steps and the several rings in each step are kept of the same size. Thus in the example shown in the figure the first step consists of seven pairs of rings or stages, the next two also of seven each, the next three of four each, the next of two and so on. This is convenient for constructive reasons and gives a sufficiently good approximation to the ideal conditions as regards the relation of steam volume to blade-passage-area and velocity.

Fig. 60.—Parsons Turbine.

119. Balance of longitudinal Forces: Dummies.—Since the pressure of the steam falls progressively from left to right there is a resultant longitudinal thrust on the drum forcing it to the right, which is balanced by means of “dummy” rings C′ C″ C‴. These correspond in diameter with the several portions of the bladed drum and are connected with them by steam passages which secure that each dummy shall have the same pressure forcing it to the left as tends on the corresponding part of the drum to force it to the right. No steam-tight fit is practicable at the dummies, but leakage of the steam past them is minimized by the device of furnishing the circumference of each dummy with a series of rings which revolve between a corresponding series of fixed rings projecting inwards from the case. The dummy rings do not touch but the clearance spaces are made as fine as possible and the whole forms a labyrinth which offers great resistance to the escape of steam. Substantially the same device is employed to guard against leakage in the glands DD where the shaft leaves the turbine case. There is a “thrust block” E at one end of the shaft which maintains the exact longitudinal position of the revolving part and allows the fine clearances between fixed and moving dummy rings to be adjusted.

120. Lubrication.—The main bearings LL are supplied with oil under pressure kept in circulation by a rotary pump F which draws the oil from the tank G. The pump shaft H, which also carries a spring governor to control the speed of the turbine, is driven by a worm on the main shaft. The same oil is circulated over and over again and very little of it is consumed. No oil mixes with the steam, and in this point the turbine has a marked advantage over piston and cylinder engines, which is especially important in marine use. In small fast-running turbines each bearing consists of a bush on which three concentric sleeves are slipped, fitting loosely over one another with a film of oil between. The whole acts as a cushion which damps out any vibration due to want of balance or alignment. In large turbines this device is dispensed with and a solid brass bearing lined with white metal is employed.

121. Blades.—The blades are generally of drawn brass, but copper is used for the first few rows in turbines intended for use with superheated steam. In the most usual method of construction they are put one by one Into the grooves, along with distance pieces which hold them at the proper angle and proper distance apart, and the distance pieces are caulked to fix them. The length of the blades ranges from a fraction of an inch upwards. In the longest blades of the largest marine steam turbines it is as much as 22 in. When over an inch or so long they are strengthened by a ring of stout wire let into a notch near the tip and extending round the whole circumference. Each blade is “laced” to this by a fine copper binding wire, and the lacing is brazed. For long blades two and even three such rings of supporting wire are introduced at various distances between root and tip. The tips are fined down nearly to a knife-edge so that in the event of contact taking place at the tips between the “rotor” or revolving part, and the “stator” or case, they may grind without being stripped off. The possible causes of such contact are wear of bearings and unequal expansion in heating up. With a proper circulation of oil the former should not take place, and the clearances are made large enough to provide for the latter. Various plans have been devised to facilitate the placing and fixing of the blades. In one method they are slung on a wire which passes through holes in the roots and in the distance pieces and are assembled beforehand in a curved chuck so as to form a sector of the required ring, and are brazed together along with the supporting wires before the segment is put in place. In another method the roots are fixed in a brass rod in which cuts have been machined to receive them; in another the rod in which the roots are secured has holes of the right shape formed in it to receive the blades by being cast round a series of steel cores of the same shape as the blades: the cores are then removed and the blades fixed in the holes.

122. Drums.—In small turbines the drums carrying the revolving blades are solid forgings; in large turbines they are also of forged steel but in the form of hollow cylinders turned true inside as well as out. These are supported on the shafts by means of wheel-shaped steel castings near the ends, over which they are shrunk and to which they are fastened by screws the heads of which are riveted over. The case is of cast iron with a longitudinal joint which allows the upper half to be lifted off.

123. Governing.—The governor regulates the turbine by causing the steam to be admitted in a series of blasts, the duration of which is automatically adjusted to suit the demand for power. When working at full power the admission is practically continuous; at lower powers the steam valve is opened and closed at rapidly recurring intervals. Each revolution of the governor shaft causes a cam, attached to the governor, to open and close a relay valve which admits steam to a cylinder controlling the position of the main steam valve, which accordingly opens and closes in unison with the relay. The position of the governor determines how long the relay will admit steam to the controlling cylinder, and consequently how long the main valve will be held open in each period. In turbines driving electric generators the control of the relay-valve is sometimes made to depend on variations of the electric pressure produced instead of variations in the speed. In either case the arrangement secures control in a manner remarkably free from frictional interference, and therefore secures a high degree of uniformity in speed or in electric pressure, as the case may be.

To admit of overloading, that is, of working at powers considerably in excess of the full power for which the turbine is designed, provision is often made to allow steam to enter at the full admission pressure beyond the first set of rows of blades: this increases the quantity admitted, and, though the action is somewhat less efficient, more power is developed. An orifice will be seen in fig. 60 a little to the right of the main steam admission orifice, the purpose of which is to allow steam to enter direct to the second set of blades, missing the first seven stages, so that the turbine may cope with overloads.

124. Absence of Wear.—Owing to its low steam velocities the Parsons turbine enjoys complete immunity from wear of the blades by the action of the steam. A jet of steam, especially when wet, impinging at very high velocity against a metal surface, has considerable cutting effect, but this is absent at velocities such as are found in these turbines, and it is found that even after prolonged use the blades show no signs of wear and the efficiency of the turbine is unimpaired.

125. Blade Velocity.—Experience has shown that the most economical results are obtained when the velocity of the steam through the blades is about twice the velocity of the blades themselves, and the Parsons turbine is accordingly designed with, as far as possible, a constant velocity ratio of about this value. As already explained, it is convenient in practice to divide the expansion into a comparatively small number of steps (about twelve steps is a usual number), giving a constant area of steam passage to the first few rows, a larger area to the next few, and so on. An effect of this is that the velocity ratio varies slightly above and, below the value of two to one, but if the steps are not too great this variation is not sufficient materially to affect the efficiency.

If the spindle or drum carrying the moving blades were of the same diameter throughout, the blades at the exhaust end would have to be exceedingly long in order to give passage to the rarefied steam. By increasing the diameter towards the exhaust end the peripheral velocity is increased, and hence the proper velocity for the steam is also increased. The amount of heat drop per ring is consequently greater towards the low-pressure end: in other words, the number of rings for a given drop is reduced. Taking the turbine as a whole, the number of rings will depend on the blade velocity at each step, the relation being such that Σ𝑛V_𝑏²＝constant for a given total drop from admission to exhaust, 𝑛 being the number of rings whose blade velocity is V_𝑏. It appears that a usual value of this constant is about 1,500,000^[10] for the whole range from an admission pressure which may be nearly 200 ℔ per sq. in. down to condenser pressure.

The increased diameter at the low-pressure end not only allows the steam velocity to be increased but by enlarging the annulus enables a sufficient area of passage to be provided without unduly lengthening the blades. In the very last stages of the expansion, however, the volume becomes so great that it is not practicable to provide sufficient area by lengthening the blades, and the blades there are accordingly shaped so as to face in a more nearly axial direction and are spaced more widely apart.

The area of the steam passage depends on the angle of the blade. If the blades were indefinitely thin it would be equal to the area of the annulus multiplied by the sine of the angle of discharge, and in practice this is subject to a deduction for the thickness of the blade on the discharge side, as well as to a correction for leakage over the tips. Generally the angle of discharge is about 221/2°; and the effective area for the passage of steam is about one-third of the area of the annulus.

Fig. 61 A shows a representative pair of fixed and moving blades of a Parsons turbine, and fig. 61 B the corresponding velocity diagram for the steam, neglecting effects of friction. V₁ is the exit velocity from the fixed blades, the delivery edges of which are tangent to the direction of V₁.

Fig. 61.

The blade velocity is 𝑢 which is 1/2V₁. V₂ is consequently the relative velocity with which the steam enters the moving blades. Approximately, the back surface of these blades is parallel to V₂ , but the blades are so thick near the entrance side that their front faces have a considerably different slope and there is therefore some shock at entrance. In passing through the moving blades the relative velocity of the steam over the blades changes from V₂ to V₃. Allowing for the velocity 𝑢 of the blades themselves, this corresponds to an absolute velocity V₄, with which the steam enters the next set of fixed blades. In these blades it is again accelerated to V₁ and so on.

126. Calculation of Velocity at each Stage.—The acceleration of the steam in each row of blades results from a definite heat drop. Or, if we look at the matter from the point of view of the pressure-volume diagram, the acceleration results from the work done on the steam by itself during a drop δ𝑝 in its pressure. The amount of this work per pound is 𝑣δ𝑝 where 𝑣 is the actual volume per pound. It is convenient in practice to write this in the form (𝑝𝑣)δ𝑝/𝑝, for the product 𝑝𝑣 changes only slowly as expansion proceeds. In designing a turbine a table of the values of 𝑝𝑣 throughout the range of pressures from admission to exhaust is prepared, and from these numbers it is easy to calculate the work done at each stage in the expansion, the pressure 𝑝 and drop in pressure δ𝑝 being known. In the ideal case with no losses we should have

(V₁²−V₄²)/2𝑔＝(𝑝𝑣)δ𝑝/𝑝

or

V₁²＝2𝑔(𝑝𝑣)δ𝑝/𝑝+V₄²

where V₄ is the velocity before the acceleration due to the drop δ𝑝 and V₁ is the velocity after.

But under actual conditions the gain of velocity is less than this, owing to blade friction, shock and other sources of loss. The actual velocity depends on the efficiency and on the shape and angles of the blades. It appears that under the conditions which hold in practice in Parsons turbines it is very nearly such that

V₁²＝2𝑔(𝑝𝑣)δ𝑝/𝑝.

In this formula, which serves as a means of estimating approximately the velocity for purposes of design, it is to be understood that in calculating the product 𝑝𝑣 the volume to be taken is that which is actually reached during expansion. The actual volume is affected both by friction and by leakage and is intermediate in value between the volume in adiabatic expansion and the volume corresponding to saturation. In the case of a turbine of 70% efficiency the actual wetness of the steam is, according to Mr Parsons’s experience, about 55% of that due to adiabatic expansion in the early stages and 60% in the latest stages. In preparing the table of values of 𝑝𝑣 figures are accordingly to be taken intermediate between those for saturated steam and for steam expanded adiabatically, and from these is found as above the velocity for any given drop in pressure, and also the volume per pound, for which at each stage in the expansion provision has to be made in designing the effective areas of passage.

The blade speeds used in Parsons turbines rarely exceed 350 ft. per second and are generally a good deal less. In marine forms, where the number of revolutions per minute is limited by considerations of efficiency in the action of the screw propeller, the blade speeds generally range from about 120 to 150 ft. per second, though speeds as low as 80 ft. per second have been used.

127. Parsons Marine Turbines.—Marine turbines are divided into distinct high and low pressure parts through which the steam passes in series, each in a separate casing and each driving a separate propeller shaft. The most usual arrangement is to have three propeller shafts; the middle is driven by the high pressure portion of the turbine, and the steam which has done duty in this is then equally divided between two precisely similar low pressure turbines, each on one of two wing shafts. The rotor drum of each turbine has a uniform diameter throughout its length, but the casing is stepped to allow the lengths of the blades to increase as the pressure falls.

The casing which contains each of the two low pressure turbines contains also a turbine for running astern, so that either or both of the two wing shafts may be reversed. Steam is admitted to the reversing turbine direct from the boiler, the centre shaft being then idle. Each astern-driven turbine consists of a comparatively short series of rings of blades, set for running in the reversed direction, developing enough power for this purpose but making no pretensions to high efficiency. The astern turbine, being connected to the condenser, runs in vacuo when the ahead turbine is in use and consequently wastes little or no power.

Fig. 62.—Parsons Marine Turbine : High Pressure Part.
Upper half : sectional elevation.Lower half : external view.

Figs. 62 and 63 are sections of the high pressure and low pressure portions of a typical Parsons marine steam turbine, as designed for the three-shaft arrangement in which the low pressure portion is duplicated. In each figure A is the fixed casing and B is the revolving drum. Steam enters the high pressure turbine (fig. 62) through J and passes out through H. There are 4 “expansions” or steps, with 9 stages or double rows of blades in the first, 9 in the second, 8 in the third and 8 in the fourth, or 34 stages in all. The low pressure turbine (fig. 63) comprises 28 more stages stepped as shown in the figure. The reversing turbine which is seen on the left-hand side in fig. 63, at the place where the rotor is reduced in diameter, has 26 stages in 4 steps. These turbines have a total normal horse power of 12,500, and run at 450 revolutions per minute.

Fig. 63.—Parsons Marine Turbine: Low Pressure and Astern Part.
Upper half: sectional elevation.Lower half: external view.

128. Longitudinal Forces in Marine Turbines.—In a marine steam turbine the size of the dummy is reduced so that instead of balancing the whole steam thrust it leaves a resultant force which nearly balances the propeller thrust. Consequently only a small thrust block has to be provided to take any difference there may be between these forces. This thrust block is shown on the extreme right in each figure, beyond the gland and bearing. The dummy (at D in the figures) is made up of some 22 rings of brass fixed in the case in close proximity to the faces of projecting rings on the rotor (fig. 64) with a longitudinal clearance of 0·015 in.

Fig. 64.Fig. 65.

This form of dummy is suitable for the end near the thrust block, where exact longitudinal adjustment is possible, but the astern turbine in fig. 63 requires a different form because some longitudinal play is necessarily brought about there by differences in expansion of the rotor and stator. Accordingly, the astern dummy is of the “radial” form shown in fig. 65 where the fine clearance is round the circumference of the brass rings set in the rotor and stator alternately. The whole dummy includes about sixteen of these rings.

129. Shaft Arrangement of Marine Turbines.—Fig. 66 shows the
Fig. 66. usual three-shaft arrangement, with two low pressure turbines in parallel on the wing shafts, and one high pressure turbine, with which they are jointly in series, on the middle shaft. In very large vessels four shafts are used, and the turbines form two independent sets one on each side of the ship. The outer shaft on each side carries a high pressure turbine, and the inner shaft carries the corresponding low pressure turbine and also a turbine for reversing. This arrangement is followed in the “Lusitania” and “Mauretania” where the low pressure turbines have drums 188 in. in diameter, are about 171/2 ft. in diameter over all and 50 ft. long, and weigh 300 tons. Each turbine has 8 steps with about 16 stages in each step in the high pressure turbine and 8 in the low. They run at 180 revolutions per minute.

130. Cruising Turbines in War-Ships.—In turbines for the propulsion of war-ships it is necessary to secure a fairly high economy at speeds greatly short of those for which the turbines are designed when working at full power, for the normal cruising speed of such vessels is usually from half to two-thirds of the speed at full power.

Fig. 67.

To counterbalance the reduced blade velocity, when running under these conditions, the number of rows of blades has in some cases been augmented by adding what are called cruising turbines, which are connected in series with the main turbines when the ship is to run at cruising speed. In the three-shaft arrangement the cruising turbines are fitted on the wing propeller shafts, which carry also the low pressure and astern turbines. They form a high and intermediate pressure pair through which the steam may pass in series before going on to the main turbines. This arrangement is shown in fig. 67, where C.H.P. and C.I.P. are the two cruising turbines. In cruising at low speeds the whole group of turbines is used in series: when the speed is increased a larger amount of power is got by admitting steam direct to the second cruiser turbine; and finally at the highest speed both cruiser turbines are cut out. The arrangement shown in fig. 67 has been used in some torpedo-boat destroyers and small cruisers. In some large cruisers and battleships a four-shaft system is employed and a longitudinal bulkhead divides the whole group into two independent sets. On each of the outer shafts there is a high-pressure ahead and also a separate high-pressure astern turbine. On each of the inner shafts there is a combined low-pressure ahead and astern turbine and also a cruising turbine. All four shafts can be reversed.

131. Application of Parsons Turbine.—The Parsons was the earliest steam turbine to be made commercially successful, and it has found a wider range of application than any other. Its chief employment is as an electric generator and as a marine engine, but it has been put to a considerable number of other uses. One of these is to drive fans and blowers for exhausting air, or for delivering it under pressure. The turbine-driven fans and blowers designed by Mr Parsons are themselves compound turbines driven reversed in such a manner as to produce a cumulative difference in the pressure of the air that is to be impelled.

An interesting field for the application of steam turbines is to economize the use of steam in non-condensing engines of the older type, by turning their exhaust to the supply of a turbine provided with an efficient condenser. It is a characteristic of the turbine that it is able to make effective use of low pressure steam. No condensing piston and cylinder can compete with it in this respect; for the turbine continues to extract heat energy usefully when the pressure has fallen so low that frictional losses and the inconveniences attaching to excessive volume make it impracticable to continue expansion to any good purpose under a piston.

132. Parsons Vacuum Augmenter.—For the same reason it is especially important in the turbine to secure a good vacuum: any increase in condenser pressure during a turbine test at once shows its influence in making a marked reduction of steam economy. In the region of usual condenser pressures a difference of 1 in. changes the steam consumption by about 5%. With this in mind Mr Parsons has invented a device called a vacuum augmenter, shown in fig. 68.

Fig. 68.—Parsons Vacuum Augmenter.

The condensed water passes to the air-pump through a pipe bent to form a water-seal. The air from the condenser is extracted by means of a small steam jet pump which delivers it into an “augmenter condenser” in which the steam of this jet is condensed. The vacuum in the augmenter condenser is directly produced by the action of the air-pump. The effect of this device is to maintain in the main condenser a higher vacuum than that in the augmenter condenser, and consequently a higher vacuum than the air-pump by itself is competent to produce. This is done with a small expenditure of steam in the jet, but the effect of the augmented vacuum on the efficiency of the turbine is so beneficial that a considerable net gain results.

133. Rateau and Zölly Turbines.—Professor Rateau has designed a form of steam turbine which combines some of the features of the Parsons turbine with those of the De Laval. He divides the whole drop into some twelve or twenty-four stages and at each stage employs an impulse wheel substantially of the De Laval type, the steam passing from one stage to the next through a diaphragm with nozzles. This form can scarcely be called an independent type. It has been applied as an exhaust steam turbine in conjunction with a regenerative thermal accumulator which enables steam to be delivered steadily to the turbine although supplied from an intermittent source. The Zölly turbine, which has found considerable application on a large scale, acts in a precisely similar manner to that of Rateau: it differs only in mechanical details.

134. Combined Reciprocating and Turbine Engines.—The combination of a reciprocating engine with a turbine is suggested by Parsons for the propulsion of cargo or other low-speed steamers where the speed of the screw shafts cannot be made high enough to admit of a sufficient blade velocity for the efficient treatment in the turbine of high-pressure steam. With a small speed of revolution blade velocity can be got only by increasing the diameter of the spindle, and a point is soon reached when this not only involves an unduly large size and weight of turbine, but also makes the blades become so short (by augmenting the circumference of the annulus) that the leakage loss over the tips becomes excessive. This consideration confines the practical application of turbines to vessels whose speed is over say 15 knots. But by restricting the turbine to the lower part of the pressure range and using a piston and cylinder engine for the upper part a higher economy is possible than could be reached by the use of either form of engine alone, the turbine being specially well adapted to make the most of the final stages of expansion, whereas the ordinary reciprocating engine in such vessels makes little or no use of pressure below about 7 ℔ per sq. in.

135. Consumption of Steam in the Parsons Turbine.—In large sizes the Parsons turbine requires less steam per horse-power-hour than any form of reciprocating engine using steam under similar conditions. Trials made in April 1900, by the present writer, of a 2000 h.p. turbine coupled to an electric generator showed a consumption of 181/4 ℔ per kilowatt hour, with steam at 155 ℔ per sq. in. superheated 84° F. Since 1 kilowatt is 1·34 h.p. this consumption is equal to 13·6 ℔ per electrical horse-power-hour. The best piston engines when driving dynamos convert about 84% of their indicated power into electric power. Hence the above result is as good, in the relation of electric power to steam consumption, as would be got from a piston engine using only 11·4 ℔ of steam per indicated horse-power-hour. An important characteristic of the steam turbine is that it retains a high efficiency under comparatively light loads. The figures below illustrate this by giving the results of a series of trials of the same machine under various loads.

Load in kilowatts.		1450	1250	1000	750	500	250
Steam used per kilo- watt-hour in pounds	$\scriptstyle {\left.{\begin{matrix}\ \\\ \end{matrix}}\right\}\,}$	18·1	18·5	19·2	20·3	22·6	34·0

Still better results have been obtained in more recent examples, in turbines of greater power. A Parsons turbine, rated as of 3500 but working up to over 5000 kilowatts tested in 1907 at the Carville power station of the Newcastle-on-Tyne Electric Supply Company, showed a consumption of only 13·19 ℔ of steam per kilowatt-hour, with steam of 200 ℔ pressure by gauge and 67° C. superheat (temperature 264·7° C.), the vacuum being 29·04 in. (barometer 30 in.). It is interesting to compare this performance with the ideal amount of work obtainable per pound of steam, or in other words with the ideal “heat drop.” At the temperature and pressure of supply the total heat I₁ is 709. After expansion to the pressure corresponding to the stated vacuum (0·96 in.) the total heat of the wet mixture would be 486, the dryness being then 0·792, if the expansion took place under ideal adiabatic conditions. Hence the heat drop I₁−I₂ is 223 units, and this represents the work ideally obtainable under the actual conditions as to temperature and pressure of supply and exhaust. Since 1 kilowatt-hour is 1896 thermal units (℔–degree C.), each pound of steam was generating an amount of electrical energy equivalent to 1896/13·19 or 143·7 thermal units, and the electric output consequently corresponds to 641/2% of the ideal work. If we allow for the loss in the electric generator by taking the electrical output as 92% of the mechanical power, this implies that 70% of the ideal work in the steam was mechanically utilized.

136. Torsion Meters for Power.—No measurement corresponding to the “indicating” of a piston engine is possible with a steam turbine. In the tests that have been quoted the useful output was determined by electrical means. Direct measurements of the useful mechanical power (the “brake” power) may, however, be obtained by applying a torsion dynamometer to the shaft. Devices are accordingly used in marine turbines for determining the horse-power from observations of the elastic twist in a portion of the propeller shaft as it revolves. In Denny & Johnson’s torsion meter two light gun-metal wheels are fixed on the shaft as far apart as is practicable, generally 15 or 20 ft., and their relative angular displacement is found by comparing the inductive effects produced on fixed coils by magnets which are carried on the wheels. In Hopkinson & Thring’s torsion meter a short length of shaft—a foot or so—suffices. A small mirror is carried by a collar fixed to the shaft, and a second collar fixed a little way along is geared to the mirror in such a way as to deflect the mirror to an extent proportional to the twist: the deflexion is read by means of a lamp and scale fixed alongside. As the shaft revolves the light reflected from the mirror is momentarily seen at each revolution and its position along the scale is easily read. (J. A. E.)

↑ From Greenwood’s translation of Hero’s Pneumatica.
↑ Savery was born probably in 1650 and died in 1715. See Sir E. Durning Lawrence’s presidential address to the Royal Institution of Cornwall (Journ. of the Roy. Inst, of Cornwall, No. li.), republished with a reprint of Savery’s Miner’s Friend of 1702, in which he discusses the originality of Savery’s invention and dismisses the claims put forward for Lord Worcester.
↑ For an account of Papin’s inventions see his Life and Correspondence, by Dr E. Gerland (Berlin, 1881).
↑ An interesting detailed narrative of the steps leading to his invention was written by Watt as a note to the article “Steam Engine” in Robison’s System of Mechanical Philosophy (1822). See Ewing, The Steam Engine and other Heat Engines, pp. 15–19.
↑ R. Mollier, Neue Tabellen und Diagramme für Wasserdampf (Berlin, 1906). See also Ewing’s Steam Engine (3rd ed., 1910).
↑ See also “Report of Steam Engine Research Committee,” Inst. Mech. Eng. (1905).
↑ Zeuner, Treatise on Valve Gears, trans, by M. Müller (1868).
↑ Proc. Inst. Civ. Eng., liii. 3, p. 50.
↑ Proc. Inst. Mech. Eng. (1883).
↑ Speakman, “The Determination of the Principal Dimensions of the Steam Turbine with special reference to Marine Work,” Proc. Inst. Engineers & Shipbuilders in Scotland (October 1905). On this subject see also Reed, “The Design of Marine Steam Turbines,” Proc. Inst. Civ. Eng. (February 1909).

[1] From Greenwood’s translation of Hero’s Pneumatica.

[2] Savery was born probably in 1650 and died in 1715. See Sir E. Durning Lawrence’s presidential address to the Royal Institution of Cornwall (Journ. of the Roy. Inst, of Cornwall, No. li.), republished with a reprint of Savery’s Miner’s Friend of 1702, in which he discusses the originality of Savery’s invention and dismisses the claims put forward for Lord Worcester.

[3] For an account of Papin’s inventions see his Life and Correspondence, by Dr E. Gerland (Berlin, 1881).

[4] An interesting detailed narrative of the steps leading to his invention was written by Watt as a note to the article “Steam Engine” in Robison’s System of Mechanical Philosophy (1822). See Ewing, The Steam Engine and other Heat Engines, pp. 15–19.

[5] R. Mollier, Neue Tabellen und Diagramme für Wasserdampf (Berlin, 1906). See also Ewing’s Steam Engine (3rd ed., 1910).

[829f1-6] See also “Report of Steam Engine Research Committee,” Inst. Mech. Eng. (1905).

[832f1-7] Zeuner, Treatise on Valve Gears, trans, by M. Müller (1868).

[841f1-8] Proc. Inst. Civ. Eng., liii. 3, p. 50.

[841f2-9] Proc. Inst. Mech. Eng. (1883).

[846f1-10] Speakman, “The Determination of the Principal Dimensions of the Steam Turbine with special reference to Marine Work,” Proc. Inst. Engineers & Shipbuilders in Scotland (October 1905). On this subject see also Reed, “The Design of Marine Steam Turbines,” Proc. Inst. Civ. Eng. (February 1909).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]