Philosophical Transactions of the Royal Society (1665-1886)/Volume 3/Number 43
PHILOSOPHICAL
TRANSACTIONS.
Monday, Januar. 11. 1668/9
The Contents.
Some Communications,
THe Argument of Vegetation is exceeding noble, largely usefull, and worthy to be expos'd to publick consideration, and a general and accurate discussion; to the end, that where Observations are uncertain, and Experiments fickle, or failing, or casual, the various Track or operation of Nature maybe the better discover'd by the greater store of confronting Trials and Observations. 'Tis for this Reason, that we not onely suggest and disperce Inquiries upon this important Subject, but are also ready to impart such Informations, as we receive from the Curious and Inquisitive of what they have experimented and observed therein. At the present we shall insert here, what hath been communicated (upon the Queries formerly publisht) by those two Worthy and Observing persons Dr. F. Beale, and Dr. Ezerel Tonge.
To the 1. Dr. B. It will be difficult to enumerate all the Vegetables that will grow the wrong end set downwards in the ground. To mention some, besides those mention'd in that Query (viz. Elders and Briars) there are Sallies, Willows, the Black-Elder, Vines, and most Shrubs; two or three of their joynts being cover'd in the mould, and the Stem cut off near the overmost Joynt, which should be half cover'd in the mould, and the mould somewhat raised, as it spirts out and grows, Dr. Tonge agrees, saying, that Curran Trees, and such like, as are of a soft wood, and quick growers, seem most apt to this improvement.
To the 2d. Dr. B, That the branch of a Plant, being laid in the Ground, whilst yet growing on the Tree, and there taking root, being cut off whilst so growing, will grow on both ends if it be well rooted in the Propagation; and the like care had of the last knot or joynt, as was before prescribed. Dr, T. faith, that Layers of those Trees, mentioned in the former Query, will grow on both ends, and aptly parted when they have spread roots both wayes, make two plants out of each Layer.
To the 3d. Dr. B. In the Tapping of Trees, the juice certainly ascends from the root, and after 'tis concocted to partake of the nature of the Plant (which feeds as well on the Air, as the juice furnish'd through the root) it descends (as the Liquor in a Limbec) to the orifice, whence it issues. Ratray, the learned Scot, affirms, that he had calculated experimentally, that the liquor, which may be drawn from the Birch in the Spring time, is equiponderant to the whole weight of the Tree, branches, roots, and all together: Whence he inferrs, that it deserves our diligence, fully to enquire into the manifold benefits that may be made by the Tappings of all sorts of Vegetables; some at the Roots, some in the Body, either from the Bark, or the Timber; some under the chief Branches (which is noted by V. Helmont to be the proper place for the juice of the Birch;) some from the Fruit, Kernel, Blossoms, Seeds, or Husks containing seeds; as Dr. Harvy had a way of filling his Silver-box with a purer sort of Opium, taken from the Husks of Poppy seed, being prickt after some time of exudation and insolation. The like whereof may be tried upon the Male peony, and other Plants of greatest fame and vertue; as well for Gums, Colours, Odors, &c. as for famous Juices. Mr. Evelyn can acquaint you of a Receipt, which he had in Italy, as a Specifick against Feavers from the Tappings of the Elme. I hear as much praise from the Oak, for stopping the Flux of Bloud by the way of Urine, whether it proceeds from the imbecility of Nature, or from the defects in the Bladder, Reins, or other inward passages, Some say as much for the juice of the Alder (though the Dwarf-Alder hath the highest praise) to cure or stop the Dropsie. And perhaps this large Natural Limbec, where it may be had, may sometimes prove more effectual, than our little, Artificial, and more troublesome Distillations. And the Congeniality of the Sun in his alternative visits, and the assiduous intercourse of the free Air, with the Spirit of the Plant yet living and growing, may have a more effectual influence for a Specific vertue, than we are apt to imagine, Though we cannot see nor hear the Lungs of Vegetables beating, yet we may sometimes smell their Breath strong enough, both to please and offend exceedingly; as in Savin, Firrs, Cypress, Elder, Rosemary, Mirtles, and generally in all Blossomers. And some that cannot be smelt by us, may yet have a very wholsome breath. One Experiment I will here bestow on you. When both my hands were manacled for many years (and sometimes my Armes also) with deep corroding Teaters; to the blush of my many friendly Physitians, and in despight of many of the best Medicines and Purgations, all was suddenly heal'd, and hath so continued these 20 years, by the application of the Gum of Plum-trees dissolved in Vinegar. I must not forget to add, that I applyed Vine-leaves, and sometimes open'd Raisins to draw a moisture from those Teaters some few dayes before I used the Gum.
Dr. T. is of opinion, that Sap alwayes rises, and never properly descends, having onely a kind of subsiding or recidivation, which he saith he cannot call a Circulation, nor resemble to the motion of Liquors in Pellican; but rather to the sinking of Liquors in an Alembec, whilst the thinner parts are forced over the helm; yet somewhat imitating the motion of Blood in Animals, forasmuch as it continually supplies the want and expence of Sap in the exterior parts, from the slock of the sap in the Trunk, root, and branches. He understands it thus; That the Sap, necessary to the growth of the leaves, fruit, and upper branches, being dispensed and converted into the form necessary for those purposes, when the Tree is fullest of Sap, in such manner that the Sap in the innermost Coats feeds the innermost, and the sap of the outward coats the outward parts, of Fruits, &c. that which remains in the Body betwixt the several coats, and betwixt the Bark and Body, begins to condense there also, first into a Geliy, and after into Wood, Bark, Roots, &c. according to the several places to which it hath subsided. And because it condenseth faster in some parts than in others, according as they be higher or lower, (whether it be by heat or cold, or exhalation of thinner parts) the sap condensed above or below, filling less room, must needs cause the sap, which is not yet condensed, in appearance to descend or subside, and to sink as it were lower and lower in the pores of the Timber and Bark, i.e. to be less high, not descend from any place, to which it was formerly risen, unless (as in Blood-letting) when some lower part is open'd, all the sap above continually flowes thither, till the Tree be emptied, or the continual flux of the Sap (the natural Balsome of the Tree) heal the wounds, as that of the Blood does those of the Body; and so much quicker and easier, by how much the Air is more favorable, or is better kept out; which he observes for their direction, who are curious in Inoculation, as the ground of their successes or miscarriages.
The Trees observ'd by the same Dr. T. to run, are the Vine; the Birch plentifully, at body, branches, and roots; the Walnut-tree, at the roits and pruned branches; some Willows and Sallyes and some sorts of Maple; the Sycamore, which is the greater Maple (some call it the Plane) at a gash made on the bark of his body, and at the root and branches; the Poplar and Asp: The Elme and Oake are referr'd to tryal; concerning which laik some Wood-men affirm, that in such of them as are Windshaken, that have large hollownesses in their Armes and Bodies, they have found great quantity of sap in the cutting of them, whereof having drunk, they quenched their thirst without any prejudice. To these add the Whitting, or Quicking-tree, (Lat. Fraxinus Sylvestris, and by some Fraxinus Cambro-Britannica) which in its season, as some affirm, will run plenteously, and whence they would have us expect a soverain Drink against some stubborn distempers, especially such as are Scorbutical and Splenetick, I have kept (faith Dr. T.) some of the juice of the Berries (which being express'd ferments of it self) these two years in Bottles, and it hath now the taste of an austere Cyder: And I suppose from its gratefull smell, that it may be kept till it ripen and become a strong Vinous Liquor. It is the Houshold drink of some Families in these parts about Wales and Herefordshire, and some out of Curiosity have brew'd ripe Berries with strong Beer and Ale, and kept it till it transcended all other Beer in goodness.
Dr. Tonges attempts upon the Poplar, Aspe, Elme, Oake, Ashe, Elder, Whitting-berry or Quicking-tree, Thorn, Buckthorn, Tile, Nut, Sloe, Briar, Bramble, &c. have not succceded; and he doubts, that they, and all Apples and Pears have some degree of Gummines in their ]uices, so that they will not run.
To the 4th Query, Dr. B, Apparently the sap riseth by the inward Birk, where you may see the quick begin, and where the Graft first incorporateth.
Dr. T. There are Circles observ'd in Trees, which are the distances of those Films or Coats, by which the Tree receives its yearly increase in thickness. Through these, looking full of Circular Pores, the Sap seems to ascend in the same manner between coat and coat, as between the Birk and the Body; and probably between the two outermost of these Coats, as large a quantity of Sap, as between the Bark and Body. Now the Ascent of Sap is by all parts and pores of the Tree, in such small quantities, as can hardly be discerned, unless the Tree be quite saw'd off, especially near the Root; for then it will appear, how it ascends. In Birches, and such like, the Sap issues very plentifully in all parts of the body, when they are cut down near the Root. And in other Trees that have Pith, as the Willow, &c it may be observ'd, when they are saw'd asunder near the Root, whether any Sap issues or no by the Pith.
The Bark is double outward and inward. The outward is dry, and in some Trees rough. The inner, is probably superadded new Coat of that years growth, or something like it, between the nature of Wood and Bark. The sap rises within and without that super added Coat.
From hence it may be more carefully inquired than hath been hitherto done. 1. Whether the more Circles there be in any Branch, the longer the Sap will ascend into it? 2. Whether the fewer Circles there are in it, the sooner the Sap subsides from it? 3. Whether a Branch (suppose) of three Circles, cut at Spring, the sap ascending, or another of the same bigness, will at Michaelmas following, if cut again, be found to have increased one or more Circles than it had in the Spring: and whether at Spring or Fall, or at other season, it be found to have a Circle or half a Circle of Pricks next or betwixt the Barks, or a Circle of Wood next the inner Bark onely, or both? But here the Comparison is to be made with distinction, For it must be inquired, Whether some Trees shoot new Tops every year until a certain Age, and after not? Whether some have the Circles in their Branches decreased from their Body to the extremity of the Branch in such order, that (e. g.) an Apple-tree shoot of this year hath one Circle of Pricks or Wood plac'd in the Graft of two years old, and that of two years growth will the next year have one Circle more then it had the year before? And whether this onely be till the Branch shoot no more Grafts, and whether then the utmost Twig get any new Circles, or stand at a stay, being nourish'd onely, not augmented in bulk as to the appearance of the Circles? And whether an Augmentation be between every Coat, or upon the outward Coat onely? Here it ought also to be enquired, Whether the Circles of pricks do encrease till Midsummer, and the Circles of wood from after Midsummer till next Spring?
Further, to perfect the experiment about Sap, and to find, Whether it ascends more or less in the prickt Circles of the Body, than in those betwixt the Body and the Bark; let the Tree be first pierced with an Auger onely through the Bark, and the quantity of Sap it yields in an hour, exactly measur'd and weigh'd; Then at the same time let another hole be bored into the Body of the Tree above an inch and an half deep, and so round about on every side of the Tree, some deeper, and some shallower, with a good large Auger; and one quite through sloaping. From which Experiment, after various tryals, may be found the difference of the Sap rising on the North and South, and so likewise of that which comes from the Bark onely peel'd off, and that which ascends in the inner part of the Tree. The weight also may be compared of that which issues from the Bark, with that, which issues from the Body, The internal Heart-sap may also be drawn apart, by boring a smaller Auger-hole in the middle of a greater, and fitting it with a long pipe, adjusted, to that inner orifice. If no difference be found in these, the presumption will be greater, that the difference of Heart (as when they call heart of Oake) and Sap in Timber is not from the plenty or scarcity of sap, but from the season of felling. This Interception of the Heart-sap may have an effect analogous to the boring out the Heart.
To the 5th. Dr. B. faith; I answer Experimentally, That if a Circle be drawn round about any common English Tree, as Oak, Elme, Poplar, &c, by Incision to the Timber (how thin soever the Knife be) so that no part of the Rind or Bark to the very solid Timber be un-cut, the Tree will die from that part upwards. Onely the Ashe, (of all that I could try) will grow on, and prosper notwithstanding the incision. My Brother (T. B.) shew'd me some old and huge Ashes, which were bared of the Bark by the Deer, from the root 4 feet upwards quite round; yet they had continued their growth many years, and some parts of the Bark, which were left in few places not so broad as the palm of my hand, had a fresh verdure more lively then the parts of the Bark which remain'd above the baring. Yet if some Incisions by hackings be made, or if the Branches of some Fruit-trees (especially the Gennet-moyle) be quite bared under a knot near the body of the Tree, and that knot and bare part be well cover'd with loame or good mould in June, that branch will not onely survive, but will be apt to take root and become a young Tree of speedy growth, if cut off below the baring, and set at a fit depth at the end of Autumn, or about Candlemas rather. Where such transverse hackings are made, or Contusions in the Bark, many Vegetables are apt to gather knobs; and sometimes small branches will spirt out above, and sometimes about the part contused. To get the Gum of Plum-trees, I have sometimes wrench'd the branch, till the solid Timber hath crackt, and the Rind forc'd open in some parts; so leaving it to grow, but forc'd to continue in a posture somewhat wreathed, it hath not fail'd to yield me store of Gum next Summer.
Dr. T. A Branch, whose Bark of the breadth of about 2 or 3 Inches is taken off round towards the bottom, in some Trees, and particularly the Lime-tree, will live, and bear leaves for many years, and grow, as other branches, by means of the sap ascending through all the pores of the inner Coats, as was said above to the 3d Q. And it ought to be well observed, in what other Trees this will hold, and especially, whether it will not hold in all Trees, whose sap runs not out very plentifully: for, in such Trees, wherein there is a plentiful Issue of the Sap between the Bark and Body, probably the Branch will die; besides, some Air, as that of North and North-East, presently blasts open'd Trees.
To the 6th. Dr. B. Concerning the Use of the Pith in Vegetables, as whether the Juyce ascends or descends by it? It may be consider'd, That my Answers above do import that the Juyce, which descends by Tapping, and which maketh the pulp or coat of any fruit, ascends by the Bark or Rind of the Plant, not by the Pith. I now add (which I can affirm by many Experiments) that the Pith, and the Timber have some correspondence with the Seed of the Plant, to conveigh an ente course of the same Spirits and nature from the Root to the Seed.
The Experiments themselves, whereby the Worthy Doctor maketh this out, we must refer to another opportunity; as also his considerable Discourse already in our hands, giving Instances to shew, That there is a peculiar Correspondence, not onely between the Seed and the Pith, Heart or Timber of Plant; but also betmeen the Bark or Sap in the Bark, and the Pulp of the Fruit, or some encompassing Coat or Husk, or Cod, which contains the Seed.
Dr. T. answers to the same Q. Piths are of a very different nature and substance. In the Walnut, is a multitude of films manifestly distant from one another. In others, as in Elders and Briars, 'tis a continued, soft, loose, dry substance. In the Walnut, an observation may be made, by cutting a small and young branch, which hath the largest pith, in March, to the Pith in some branches, and through it in others of the like bigness: Whether any Sap issues out or no by the Pith, will be found by the quantity of the Sap issuing from the one and the other compar'd.
The Observations also of the Effects of Boring and Pegging the Pith, are reserv'd to the like tryal about the same time. But 'tis probable, that if the whole Pith be forc'd out, the place so bor'd will be fill'd with Sap, which will gelly there, and at length be converted into wood; as 'tis conceiv'd it does yearly between the abovesaid films, coats, and in all the pores of the Body of the Tree, and in those of the Bark proportionably, For, the Sap issuing from the Birch, cut down, turns into a white Gelly on the head of it; and likewise in those holes that are bor'd in the body of the Birch about March, by which the Tree receives its growth in all its parts.
To the 7th. Dr. Tonge, The points or ends of the Roots being cut off, they will in proportion bleed as copiously, as the Branches, and probably more; certainly longer, because there is greater plenty of juice ascended above them, than the Branches, and consequently more will issue by them, than by any part of the Tree, higher then them.
To the 9th. The same. Trees in their full growth, or near it, will probable yield more sap.
To the 10th. The same. From the latter end of January, to the middle of May, Trees will bleed. Those, that are said to run first are the Poplar, Aspe, Abele, Maple, Sicamore; some, as Willows, and the Birch, tried by my self, are best to tap about the middle of the second season; and the Walnut towards the latter end of March, They generally bleed a full Month in the whole. Mr. Midford of Durham, a very expert Gatherer and Preserver of Saps, affirms, that the Saps of the Poplar and Aspe rise so briskly in January, that they will bleed before the end of that Month. The Sycamore will run in hard frost, when the Sap freezes, as it drops. Fiat Experimentum, Since we are now in that very season, to see whether that early ascent is to be imputed to the forwardness of the year, or not? Let it also be observed, whether the Sap ascends in Oak and Elme, at any time in this month of January; and likewise, which of these three, the Maple, Sally, or Willows, be the most early in yielding of Sap?
And to obtain an Universal and Accurate knowledg of the nature of Sap in Trees, its properties and accidents; Observations and tryals must be made by a Number of men, that have leisure to attend that business daily which are to examine concerning every Tree;
1. Its Age, Soyle, Situation, &c. the variety of the Ascent of the Sap depending thereon, as on the nature of the Tree it self.
2. The different time of Ascent in Branches, Body, Roots; and of its distilling from cut branches; from roots, not from branches.
3. The Seasons and differences of the time of the year, month and day, in which these accidents happen or cease; whereby it may appear, what to determine concerning them: And particularly, whether that conjecture be well-grounded, which supposes, That Sap does not descend from Trees otherwise than by jellying so as to fail above, whilst there is yet plenty below; as seems to be manifest by the running in the Roots, when it ceases in the Branches.
It were also not amiss to observe, Whether in any Trees, the Sap as to its ascending, keeps time with the Suns entrance into this or that Sign?
To the 11th. The same. The best time of the day for Tapping, is about Noon. In the latter season, when Sap is not very plenteous in Trees, they will neither run morning, not evening, nor probably at any time of the night; but when they are very full of Sap, and emptied but by small vents, the Sap may run night and day, till exhausted; but never in large vents.
Quere, Whether this Observation may not give light to that Opinion, which holds, that the Ascending of the Sap depends upon the Pressure or Pulsion of Heat, striking the Earth, and thereby driving the moisture of the Earth into the Root?
To the 12th. The same. Trees afford no juice at all (that has been observ'd) in Autumne.
To the 13th. The same. Rain being fearce, the juice will be fearcer. Plenty of Rain can onely give such plenty of Sap, as the pores will admit.
The Answers to the rest of the Queries we reserve for another Month, least these Paper be altogether filled with one subject. Those that have been deliver'd here from Dr. Tonge were for the rnost part taken out of his Letters to Sir R. Moray, in January, February, March, Aprill, 1666; at which time he had newly made Experiments about Saps; and are now, after conference with him, accommodated to the Queries formerly made publick.
Answers
1. The greatest length of time, that Pearl-divers in these parts can hold under water, is about a quarter of an hour; and by no other means but Custome: For Pearl-diving lasteth not above Six weeks, and the Divers stay a great while longer under water at the end of the Season, then at the beginning. Here at Batavia is an expert Diver, who draws wages for nothing else but for diving for Anchors, Guns, &c. lost in the Road. I have seen him several times go down, holding my breath as long as I could, but he stay'd ten times as long under water, as l could hold my breath. But he will not go down, unless you give him a whole Pint of Strong-water.
2. The Oyle drawn out of the Roots of Cinamon-trees, and resembiing Camphir, is thence extracted, the Roots being dried, bruis'd, and steep'd in water, and then drawn over by an Alembec.
3, The Ligmum Aloes is the part of a Living Tree, but commonly found, when 'tis wither'd: The Tree it self is of a white soft wood, giving a milky juice, which is so venemous withal, that if in cutting the Tree, any of the milk light in your eye, you grow blind; if on any other part of the Body, it becomes scabby, and noysomly sore. The Lignum Aloes, or Calambac, is found within the White-wood, but not every where. When the Tree decays, the White-wood soon withers, and grows worm-eaten, and the Milk so dries up, that you may easily rub it asunder with your hand. The best is found in the midst of the Tree nourish'd by the Heart-root, which goes streight down into the ground.
4. The Wood, stinking like humane Excrement, grows thus naturally in the lsles of Soler and Timor, and thereabouts.
5. There are indeed such Serpents in these parts, which have an Head on each end of their Body, called Capracapelle. They are esteem'd Sacred by these people, and fortunate to those in whose house and lands they are found; but pernicious to whornsoever doth them harm. I would have sent one, but could get no man that would kill them.
These Answers were accompanied with divers Curiosities, sent over by the same Generous Person for the Repository of the R. Society; among which were the Pictures of the true Musk-Dear, and of divers Aromatical, and other East-Indian Vegetables, and particularly of the Nutmeg called Thee-ving; because that being put amongst a whole room full of good Nutmegs, though it be but one it will corrupt them all: Besides a very fragrant Oyle drawn out of the bark of a Tree (called Lawang:) and some of the Blood of a Fish, call'd Bedille, esteem'd very excellent against Fluxes of Blood. Together with which should have come a sort of Beans growing on the Coast of Coremandel, having this quality, that the inside of an Earthen Vessel being rubb'd therewith, the most muddy water powred into it, will precipitate all its muddiness; but this was lost by the way. 'Mean time care is taken to procure some others of that kind, to make the Experiment here.
A Summary Account given by Dr. John Wallis,
PEtis, V. C. ut quæ mea sunt de Motibus æstimandis Principia, paucis aperirevelim. Id autem, si meministi jam olim factum est, non modo in illo Opere, quod ante octo menses R. Societati exhibitum, eorum jussu prælo subjectum est; sed & jamdudum in duobus scriptis eidem Societati ante plures Annos exhibitis, quæ & Te penes sunt: Quorum alterum, ex generalibus Motus Principiis, rationem reddit, qui fieri possit, ut Homo flatu suo (Vesicam inflando) saltem Centipondium elevare potis sit (quod Experim. ante 16. vel 18. annos Oxoniæ exhibitum, coram Ipsis aliquoties fuit repetitum;) Alterum, varia de Experim. Torricelliano dicto, Phænomena, ex principiis Hydrostaticis exponit.
Summa rei huc redit:
1. Si Agens ut A eflicit ut E; Agens ut 2 A, efficiet ut 2 E; 3 A, ut 3 E, &c. cæteris paribus: Et, universaliter, m A ut m E; cujuscunq; rationis Exponens sit m.
2. Ergo, si Vis ut V moveat Pondus P; vis m V ut movebit m P, cæter. paribus: puta, per eandem Longitudinem eodem Tempore, h.e. eadem Celeritate.
3. Item, si Tempore T. moveat illud per Longitudinem L, Tempore n T movebit per Longitudinem n L.
4. Adeoque, si Vis V, tempore T; moveat Pondus P, per Longitudinem L; Vis m V, Tempore n T, movebit m P, per Longitud. n L. Et propterea, ut V T (factum ex viribus & tempore) ad P L (factum ex. pondere & Longitudine) sic m n V T, ad m n P L.
5. Quoniam Celeritatis gradus sunt Longitudinibus eodem Tempore transactis Proportionales, feu (quod eodem recidit) reciproce Proportionales Temporibus eidem Longitudini transigendæ impensis: erit h. e. Gradus Celeritatum, inratione composita ex Directa Longitudinum & Reciproca Temporum.
6. Ergo, propter erit h.e. .
7. Hoc est, si Vis V movere potis sit Pondus P, Celeritate C: Vis m V movebit vel idem Pondus P, Celeritate m C; vel eadem Celeritate, Pondus m P; vel denique quodvis Pondus ea Celeritate, ut factum ex Pondere & Celeritate sit m P C.
8. Atque hinc dependet omnium Machinarum (pro facilitandis motibus) construendarum ratio: nempe, ut qua ratione augetur Pondus, eadem minuatur Celeritas; quo fiat, ut Factum ex Celeritate & Pondere, eadce Vi movendo, idem sit: puta
9. Si Pondus , Vi , Celeritate , latum, in pondus Quiescens (non impeditum) directe impingat; ferentur utraque Celeritate . Nam, propter eandem Vim, majori Ponderi movendo adhibitam, eadem ratione minuetur aucti Celeritas: nempe . Adeoque Alterius Impetus (intellige factum ex Pondere & Celeritate) fiet ; Reliqui .
10. Si in Pondus , (Vi ) Celeritate latum, directe impingat aliud, eadem via, majori Celeritate infequens; puta Pondus , Celeritate , (adeoque Vi latum; ferentur ambo Celeritate . Nam Adeoque præcedentis Impetus fiet ; subsequentis, .
11. Si Pondera contrariis Viis lata, sibi directe occurrant sive impingant mutuo, puta, Pondus (Vi ) Celeritate , dextrorsum; & Pondus , Celeritate (adeoque Vi ) sinistrorsum: Utriusque Celeritas, Impetus, & directio, sic colliguntur. Pondus dextrorsum latum, reliquo si quiesceret, inferret Celeritatem , adeoque Impetum , dextrorsum, sibique retineret hanc eandem Celeritatem, adeoque Impetum dextrorsum (per Sect. 9.) Pondusque sinistrorsum latum (simili raione) reliquo si quiesceret, inferret Celeritatem , adeoque Impetum sinistrorsum; sibique retineret hanc eandem Celeritatem, adeoque Impetum sinistrorsum. Cum itaque motus utrinque fiac; Impetus dextrorsum prius lati, jam aggregatus erit ex dextrorsum, & sinistrorsum; adeoque re adse vel dextrorsum vel sinistrorsum, prout ille vel hic major fuerit, eo impetu qui est duorum differentia: h.e. (posito signo dextrorsum, & sinistrorsum significante,) Impetus erit ; Celesitas ; (adeoque Dextrorum vel sinistrorsum, prout 1 vel major feurit.) Et similiter Impetus sinistrorsum prius lati, erit ; Celeritas : Adeoque dextrorsum vel sinistrorsum, prout 1 vel major fuerit.
12. Si vero Pondera nec eadem directe via procedant, nec directe contraria, sed oblique sibi mutuo impingant; moderandus erit præcedens Calculus pro obliquitatis mensura. Impetus autem oblique impingentis, ad ejusdem Impetum qui esse si directe impingeret (cæter. paribus) est in ea ratione qua Radius ad Secantem anguli Obliquitatis; (Quod etiam intelligendum est, ubi Perpendiculariter, sed Oblique cadiy in percussi superficiem non minus quam ubi viæ motuum se mutuo Oblique decussant:) Quæ quidem Consideratio, cum Calculo priori debite adhibita, determinabit, quænam futura sint sic Oblique impingentium Celeritas, Impetus, & directio, h. e. quo Impetu, qua Celeritate, & in quas partes ab invicem resilient, quæ sic impingunt. Eademque est ratio Gravitationis gravium Oblique descendentium, ad eorundem Perpendiculariter descendentium Gravitationum. Quod alibi demonstramus.
13. Si quæ sic impingunt Corpora, intelligantur non absoture dura (prout hactenus supposuimus) sed itan ictui cedentia, ut Elastica tamen vi se valeant resticuere, hinc fieri poterit ut a se mutuo resiliant ea corpora, quæ secus essent simul processura; (& quidem plus minusve, prout hæc vis restitutiva major minorve fuerit,) nempe si Impetus ex vi restitutiva sit progressiva major.
In motibus acceleratis & retardatis, Impetus pro singulis momentis is reputandus est, qui gradui Celeritatis tum acquisito convenit. Ubi autem per Curvam sit motus, ea reputanda est, in singulis, punctis, mocus directio, quæ est Rect ibidem Tangentis. Et si quando motus tum acceleratus vel retardatus fit, tum & per Curvam fiat (ut in Vibrationibus Penduli;) Impetus æstimandus erit, pro singulis punctis, secundum tum gradum accelerationis, cum Obliquitatem ibidem Tangentis.
Atque hæc sunt (quantum Ego judico) Generales Motuum Leges; quæ ad Casus particulares Calculo sunt accommodandæ. Quos tamen, si sigillatim persequi vellem Epistolæ limites transilirem: Neque commode sieri potest seire Schematum apparatu, quibus hic abstinendum putavi. Vale. Oxon. d. 15. Novemb. 1668.
Lex Naturæ de Collisione Corporum.
VElecitates Corparum propriæ & maxime Naturales sunt ad Corpora reciproce proportionales.
| Lex Naturæ | Itaque Corpora R. S. habenia proprias Velocitates, etiam post Impulsum retient proprias. | |
| Et Crorpora R. S. improprias Velocitates haebntia ex Impulsu restituuntur ad Æquilibirum; hoc est, Quantum R superat, & S deficit à propria Velocitate ante Impulsum, tantum ex Impulsu abstrahitur ab R & additur ipsi S & e contra. |
Quare Collisio Corporum proprias Velocitates habentium æquipollet Libræ escillanti super Centrum Gravitatis.
Et Collisio Corporum improprias Velocitates habentium æquipollet Libræ super bina Centra æqualiter huic inde à Centro Gravitatis distantia: Libræ verro Fugum, ubi opus est, producitur.
Itaque Corporum æqualium improprie moventium tres sunt casus. Corporum vero inæqualium impropriæ moventium (sive ad contrarias sive ad easdem parters) decem sunt omnino Casus, quorum quinque oriuntur ex Conversione.
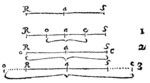
R S Corpora æqualia, vel R corpus majus, S corpus minus.
a Centrum Gravitatis sive ansa Libræ. Z summa velocitatum utriusque corporis.
| R e | veloc. corp. | R | ante impulsum data | vel | S o | veloc. corp. | S | ante impuls data. | ||||||||
| S e | S | R o | R | |||||||||||||
| O R | veloc. corp. | R | post impuls. quæsita | e S | veloc. corp. | S | post impuls quæstia. | |||||||||
| O S | S | e R | R |
[Lege syllabas (quamvis disjunctas) R e S e o R o S vel R o S o e S e R in Linea cujuslibet Casus, & harum quæ scribitur in Schemate more Hebraico. ea indicate motum contrarium motui, quem notat cujusvis syllabæ scriptio Latina. Syllaba conjucta quietem Corporis denotat.]
| Calculus | . | ||||
| . |
Natura observat regulus Additionis & Subductionis Speciosæ.
An Account of two Books.
THese Observations of the Nobie Tycho, as they were procured and preserv'd by those Three Mighty Emperours, RUDOLPH. II. FERDINAND. II. and III; so they were lately by the Command of his Imperial Majesty LEOPOLD made publick. They are usher'd in by a Liber Prologomenos, compendiously representing the Observations made from the time of the very Infancy of Astronomy unto that of its Restauration by the Illustrious Tycho, and reduced into 7. Classes, viz.
1. The Babylonian Observations; from A. before Christ 721, unto A. 432.
2. The Grecian; from A. before Christ 432, unto the beginning of the Vulgar Christian Account.
3. The Alexandrian; from A. Christi 1. until A. 827.
4. The Syro-Persian; from A. C. 827. unto 1457.
5. The Norimbergian; from A. C. 1457. unto 1509.
6, The Borussian; from A. C. 1509. to 1529,
7. Mixt Observations; from A. C. 1529. to 1582.
In which year (1582) do begin the Observations of Tycho (as is affirm'd in this Edition) contain'd in 20 Books, and made in as many years, ending An. Chr. 1601, which was the end of Tycho's Life: Of which time yet there being wanting one year (viz. 1593) of the Brahean Observations, that is supply'd by the Hessian; and by a Catalogue of the Fixt Stars, made and digested by the Authority and Care of that Renowned Prince for Learning and Magnanimity, William, Landgrave of Hessen, and by the Labours of Rhotmannus and Birgius.
To all these is added a Continuation of such Astronomical Observations as were made from the time of Tycho's death unto An. 1635, by Mæstlinus and Schickardus.
Having given the Reader this short Account, I find my self obliged to give him notice withall of a Paper publish'd this year, entitled Specimen Recognitionis nuper editarum Observationum Astronomicarum, Nob. Viri Tychonis Brahe, printed at Copenhagen in 4°: wherein are remark'd by Erasmius Bartolinus the more considerable Errors in the Observations of An. 1582. In this Edition of the Histor. Cælestis, by comparing it with the Orginal, in the power of the present King of Denmark. In which Paper hopes also are given of a more correct Edition, and that of the Original itself; together with the Observations both from An. 1563. to An. 1582. and those of An. 1593; all wanting in this Edition of Ausburgh.
THese Works contain,
1. Of Astronomy 8 Books, wherein the Author hath explain'd the whole Doctrine of that Science in such a gradual Scientifick Order, that now (as himself in his own Preface intimates) a Student 'without the Aid of a Master may learn the whole by his own Study, which was formerly not easie to attain with the best Instructions.
It may be, the Inquisitive Reader will be desirous to know, what Systeme of the World it is, this Author insists on; concerning which we shall give you his own words, p. 326.
Hanc controversiam (sc. de Motu Terræ) Joh. B. Ricciolus Almag. l. 9. ea tum eruditione tum copia prosectus est, ut facile omnes in hoc negotio superaverit. Primo, Copernicanorum pro Motu Terræ Argumenta 49. deducit ac destruit; pari deinde cura, quæ contra Terræ Motum afferri solent & possunt Argumenta, vid. 77. recenset. Mihi vero, cum nihil hactenus in utramvis partem adductum videam, quod Probabilitatis metam excedat, hic immorari non est enimus. Unum est tamen ex omnibus contra Terræ Motum ipsius Riccioli Agrumentum a Gravium descensu petitum, cui vim ipse Demonstrationis inesse putat; quod examinare hoc loco accuratius opera pretium judicavi.
This with other Arguments he refutes; but declareth p. 330. That, though he knows no Argument, demonstrating the Rest of the Earth and Motion of the Sun;, yet the Authority of Holy Writ, now seconded by that of the Sacred Congregation of the Cardinals, put it out of doubt.
Concerning the Doctrine of Motion, the Author saith thus, p. 15. Motuum Compositorum Contemplatio dignasane este, quæ a Geometris excolatur. De solo motu Volutionis conscripsi Tract atum integrum, quem cum libris Cylindricorum & Annularium in lucem edidi. De Motu Projectorum, qui & ipse Compositus est, subtilissimi exstant Libri Galilæi & Torricellii: Et præter hæc, alia supersunt innumera, de quibus integra Nova Scientia condi possit. (Which is accordingly done by the Excellent Dr. Wallis in his Book now in the Press.)
For the case of Calculating an Eclipse of the Sun, we find, that this Author p. 177. determines, in what part of the Earth such an Eclipse shall appear, without the Aid of Parallax, and that the Sun's Parallax, as to the determination of Celestial Motions, may be safely neglected. And p. 40. he rejects the Sensible Inequality of the Solar or Tropical years; as also p. 60. the Irregularity of the Obliquity of the Ecliptick, of the Procession of the Equinoxes and Excentricity. Pag. 127, he solves that Doubt of Ricciolus, That it cannot be exactly and evidently known by any Natural Observations made of the Moon or any Star, what the Parallax is, without the fore-knowledge of the Parallax, or distance from the Earth. And p. 193. avoids these Inconveniences in assigning the Declinations of the Fixed Stars. P. 338. this Author asserts, that the Comets and New Stars, that have appear'd since 1572, have been far above the Moon; and that Ricciolus about this Controversie seem'd too favourably inclined to Claramontius, asserting the contrary.
Concerning the Cause of the Secondary light of the Moon before and after the New, to wit, the obscure part of her appearing like kindled glittering Ashes, our Author assigns it to be the Suns rays reflected from the bright Hemisphere of the Earth to the darker portion of the Moon, and thence again directly reflected to the Earth destitute of the Sun's light. This Phenomenon he saith, is learnedly explain'd in Philos. Optica Nic. Zuccbii from p. 247 to p. 260.
The Author hath not framed nor annex'd any Tables to his Book, although he abundantly shews, How they may be computed: referring his Reader to those of Tycho, Reinholdus, Longomontanus, Kepler, Lansberg, Wendelinus, Bullialdus, Petavius, Reinerius, Ricciolus; to which may be added those of Duret, Billy, Street (which last fixes the Nodes and Aphelions) and Wings, now in the Press.
To the end of these 8 Books. are annext Proportions for the 28 Cases of Spherical Trigonometry. Those that desire to be farther satisfied, may read Trigonometria Britannica of Gellibrand and Newton, the Idea Trigonometriæ by the Lord Bishop of Sarum, Dr. Seth Ward; and also Bonavent. Cavalerii Trigonometria, and his Directorium Universale Uranometricum, but especially his Compendio delle Regole Trigonometriche & Centuria di Problemi.
2. Of Practical Geometry 3 Books.
In the First the Author handleth
The Construction of the Tables of Sines, Tangents, and Secants.
The Resolution of Right-lined Triangles.
The Mensuration of the distance of Objects, as well unaccessible as accessible.
The Heights of Mountains, Towers, Clouds, Rainbowes, the Depths of Wells and Vallies. He concludes the perpendicular height of the burning Mountain Ætna to exceed 5 Bononian Miles; of Mount Caucasus beyond the Caspian-Sea to be 51. Mount Athos of Greece 28. Casius of Syria 20. the Alpes of Italy and Pic of Tenariffe 10 Miles The Circumference of the Earth, the Distances of the Sun, Moon, and Earth.
In the second Book, he handles the Dimension of Plain Surfaces, either Regular or Irregular, and takes the Ichnography or Description in Paper, of any Figure given of the surface of the Earth: Asserts the Possibility of the Quadrature of the Circle, and handles the Transformation of Plain Figures, to wit, their Addition, Subtraction, Augmentation, Diminution, Comparison; further the dividing of a Plain Triangle, in a given Reason by a line passing through a Point any where assigned: This he doth largely in 16 Propositions, because upon it chiefly depends the Division of other Right-line Figures; and because he found divers Determinations wanting, when the point is given within. Those that are desirous to see this Analytically done, may find it in Herigon with a Construction thereof; as also a Geometrick Construction thereof in Van Schootens Miscellanea; and another most excellent Construction at the end of Van Ceulen de Circulo & Adscriptis.
Afterwards our Author proceeds to the dividing of other Figures, in a given Reason, or by parallel lines, and sheweth how to apply the whole to Practice in the Field.
In the third Book the Author first measureth such Solids as are contained under a Plain Surface. Secondly, such as are contained under a Curved Surface. Thirdly, He measureth the Mundane Bodies, as the Surface of the whole Earth; where he is pleased to conclude, that at the Day of Judgement, a less portion of it then England, will serve to hold all its Inhabitants, and their Infants, that ever have been, or in likelihood may be hereafter, till then, supposing the World should last 10000 years. He measureth also the Solidity of the Earth, and Ocean; the Magnitude of the Sun, Moon, and Earth. The Increase, and Diminution, the Transformation and Comparison of divers Solids, and the Mensuration of divers of their Surfaces.
3. Of Opticks 3 Books.
In the first, he handleth the simple and direct Appearances-of Objects meaning such appearances as are not liable to Reflection or Refraction; and herein he saith, that passing by slight matters, he onely treats of such as are either new, or of the better esteem; such as are the Properties of the sight, the manner of its perceiving a Distance; and the Place of the Eye being assigned, to find that Height, in which a greater Length or Breadth shall appear equall to a lesser Length or Breadth, or any assigned Length or Breath shall appear in a given Proportion. He likewise finds the Portion of a Cone or Cylinder; seen according to the Magnitude of the Figure, and Position of the Eye, and explains the Moons Phases.
In the 2d. He handles the Theory and Practice of the Perspective or Scenographic Projection, or Transcription of a given Magnitude into a Plain, which cuts the Optick Pyramid, wherein he explains the Direct appearance, and the Monstrous defamation of an Object, which at a certain place shall appear beautiful.
In the 3d. He treats of the Astronomick Projections of the Spheare, and thence derives the triple Astrolabe, and shews their uses, and the Conveniences or Inconveniences of each Projection: viz. the Projection on the Plain of the Æquator, the Eye being in one of the Poles; or on the Plain of the Colure of the Solstices, the Eye being in one of the Æquinoctial Points; and the Orthographick Projection, by Perpendiculars, falling from the respective Points of the Circles of the Spheare, on the Projecting Plain: Such a Projection, if the Plain be the Meridian, Ptolomy called the Analemma.
If the Eye be in the Zenith of Nadir projecting, on the Plain of the Horizon, the Author sheweth, that the Projection will be the same, as if the Eye were in one of the Poles projecting on the Plain of the Æquator, onely the names of Circles are changed.
Pag. 205. Nam Circular qui in illa referebat Æquatorem, in hac Horizontem repræsentat; & Projecturæ Tropicorum reliquorumq; Æquatori parallelorum in illa, in hac sunt Projecturæ parallelorum Horizonti seu Almicantarath: rursum qui in illa sunt Projecturæ Horizontis, Almicantarath & Verticalium, in hac projecturæ erunt Æquatoris & Parallelorum ejus, ac Meridianorum. Postremo rectæ lineæ, quæ per Centrum Projectonis ductæ, erant projecturæ Meridianorum in illa, in hæc erant Verticalium Projecturæ; quare qui illius Projectionis modum prove intellexerit, hanc qucq; nullo negotio perficiet.
if this had been well observed, there had been no need of Controverting, Whether the Horizontall Projection had been a New Invention: It is as Ancient as Ptolomy, and all the 4 Quadrants of several contrivances published by Mr. John Collins* * Those Quadrants, printed, may very conveniently be pasted on Copper-Plates, and varnisht; which done, they will be not only very cheap and portable (to be had at John Marks at the Sign of the Golden Bail near Somerset-House) but also serviceable enough, being preserv'd by the Varnish from the accidental injuries of Ink and Dirt; and for these very causes made publick, serving for an Example to introduce the like way for other Mathematical Instruments. are derived from the Western side, or the continuance thereof, admitting but a meer Mutation of the Names of Circles, and a projecting of more Parallels.
4. Of Catoptricks 3 Books; in the First of which the Author treats of Catoptricks or Reflection.
In the Second, of the affections of Plain Glasses simply, or of many focii, placed either in a Parallel or Inclined Position to each other.
In the Third, of Curved Glasses, and therein first the chief affections of Convex Sphærick Glasses; afterwards of Concave Sphærick-Glasses: lastly of Burning Glasses of several kinds.
The death of the Author prevented him from Writing of the Dioptricks which was very far advanced by Des Chartes and hath been further promoted since by De Beaune, Honorato Fabri, Manzini, and in the Century of Optick Problems of Eschinardus and we may hope that erelong the learned Mr. Barrow will enrich the World with his Labours of this and other kinds; also Mr. James Gregorie, the Author of Optica Promota, hath a Treatise of this Subject in good forwardness for the Press.
S. Follows the Authors Treatise of Military Architecture or Fortification; in which he hath collected six several ways of Regular Fortification, and hath likewise divers-ways for Irregular ones, when the Scituation of the place so requires; and intersperseth divers questions, and relates some Transactions in the late eminent Sieges of Christendome.
6. Follow his Annularia & Cylindrica; the first 4 Books, whereof were first publisht in 1651, and are common enough to he had here; which may make the Reader wonder at their being reprinted; especially considering, that though they have deservedly received much applause, yet they have likewise been censur'd for opposing and neglecting other Methods, whereby the Author might have rendred, what he delivers, more universally and briefly. Concerning the first 4 Books, Ant. Lalovera in his Book de Geometr. veterum promota thus:
Sero venerunt in manus nostras R. P. Tacqueti lib. 4. Cylindricorum & Annularium: Opus censemus absolutissimum, ejusq; Authori, qui primus hæc de re suas lucubrationes vulgavit, istam coronam debitam esse agnoscimus.
And Stephen Angeli in his Treatise de Infinitis Parabolis, deque Infinitis Solidis, &c. (printed at Venice 1659.) in the Preface begins thus;
Publici Juris fecimus elapso anno 1658. libellum quendam, cui titulus, Sexaginta Problemata Geometrica: In hujus calco Appendiculam adjunximus, in qua occurritur Mario Bettino, Calveriana Indivisibilia veluti Dæmonas paventi. Paucis vero transactis diebus a modo dicti Libelli impressione, incidimus forte Venetiis in opus Aureum And. Tacquet, CYLINDRICA & ANNULARIA nuncupatum; in quo cum incideremus in Schol. prop. 12. l. 1. Authorem carpere Indivisibilia invenimus.
Doluimus vehementer (saith Angeli) Opus tanta eruditione refertum non prius admanus nostras pervenisse; censura autem in ipso conta Indivisibilia pronunciata, parum aut nihil nos turbat: Vetera enim continet & non nis corum modica, & imbecilliora, quæ prius ab ipsp Cavalerio in Præfat. Geometriæ Indivisibilium, & a Guldino in Centro-baryca objiciuntur; quibus satis superque occurrit ipse Cavalerius.
And Angeli in the Preface of his Treatise De Infinitorum Spiralium Spatiorum Mensura (Venetiis 1660.) having occasion so mention the fruitless endeavour of Guldin in finding the Center of Gravity of a Spiral Line, and a Right line equal thereto, saith thus;
P. Guldinus, Centrobarycæ (Anno 1635. & 1640. editæ) Author famosus (at Cavalerianorum Indivisibilium contemptor & irrisor, qui dum Indivisibilius irrist, seipsum ridiculum præbuit) altius omnibus volatum sumpsit, at conatu irrito, & Icari fine, ut ipsemet fatetur.
But Guldinus doth not confess himself in an error in opposing Cavalier's Geometria Indivisibilium, publisht 1632; but saith, he was very aged, of an infirme memory, and that he had not (as we may gather) leisure to peruse it thoroughly, when he had health, nor health when he had leisure. The Controversie, and the Reply about it, is exceeding pleasant, and to be found with other considerable Miscellanies in the Geometr. Exercitat. of Cavalerius printed at Bononia 1647. Which Book if Tacquet had seen (for he quotes it not) he would probably not have made any such opposition.
Angeli doth not only answer what is objected by Tacquet, but shews, what famous Authors he hath on his side, who have derived many excellent Inventions from this Method of Indivisibles, viz. Beaugrand, Rocca, Magiottus, Van Schoten, Rich. White, Bullialdus, Torricellius, who calls Cavalieriusss First Book the Ocean of Indivisibles, and the Fountain of Inventions. Of which Doctrine he renders many excellent Examples.
Moreover the same Angeli in the Preface to his said Tract, De Infinit. Spiral. Spatiorum Mensura, hath these words:
Pro Indivisibilibus est veritas ipsa, stantque illiomnes præclarissumu Geometræ, quos in Epist. ad Lectorem Operis nostri De Infinitis Parabolis recensuimus; quibus nuper ultro se associavit Vinc. Viviani l. 1. De Maximis & Minimis, monito posf Prop. 17. ubi ait, Ut hoc loco, ex adverso indirectæ Antiquorum viæ per duplicem positionem, luce clarius pateat, quantum facilitatis, brevitatis, atgue evidentiae nanciscatur e nova directaque methodo (recite tamen cauteque usurpata) acutissini Cavalerii; per Indivisibilium doctrinam nobis amicissimam.
And when thus carefully, to apply it, of that see Lalovera's Elementa Tetragonismica Tolosæ 1651, where more Archimedo he demonstrates the truth of this Method: which Book if Angeli had seen, he would certainly have quoted it, and admired the Author.
For want of this Method, it was, saith Angeli, by way of complaint, of Tacquet, that he omitted some Theorems, which by aid thereof he might easily have found out. See him in his Preface to his Infinite spirals; but especially at Schol. 3. Prop. 15. l. 2.
Siergo Tacquet recepisset doctrinam Cavalerii, potuisset non solum Cubare portionem Cylindrici Parabolisi super quæcunque Infinitarum Parabolarum per Basin Parabolæ & Punctum in latere; sed etiam ex iis, quæ in Exercitat. 4. Cavalerii tradunt ipse & Beaugrand, potuisset Cubare Segmenta portionis cujuscunque Cylindrici Parabolici reseclæ planis sectioni maximæ parallelis: Imo ex doctrinæ Cavalerii potuisset etiam Cubare, & portionem Cylindrici super Hyperbola per basin Hyperbolæ & Punctum in latere, & segmenta hujus portionis resectæ planis sectioni maximæ parallelis (supposita tamen Hyperbolæ Quadratura.)
Angeli finds afterwards another deservedly famous Man, viz. Dr John Wallis, owning and using the Method of Indivisibles, and advancing it to admiration in his Arithmetica Infinitorum; who in his Book de Cycloide at Oxford 1659, saith thus, Pag. 9.
Supponimus enim (quodet facile, si opus est, probabitur) Planum quodvis tantundem hujusmodi Conversatione (seu Rotatione) producere, quantum est quod fit ex eodem Plano in lineam ipsius Centro grsvitatis, descripta ducto; quod & de linea quavis sive recta sive curva, in eo Plano descripta, pariter intelligendum est: Quod quidem enim ipse olim me primum invenisse putaverim, monitus moxeram, nonnihil apud Guldinum exstare quod huc spectet. Id autem si animadvertisset Tacquteus, dum de Cylindricis & Annularibus acutum Opus conscripsit, non patum illi fuisset adjumento, multique quæ illic extant, tum Universalius tum contractius forte faissent edita.
All which is not recited here, to disparage our Author, but to take off the prejudice, which he may beget in his Readers against the Method of Indivibles, which hath been owned by other famous Men, besides those already recited; viz. by Mengolus, who from the Excellencies of this Method, Archimed's Method, and Vieta's Specious Algebra, compos'd his Geometria Speciosa; by Antimo Farby, alias (as 'tis suggested) Hon. Fabri in Tract. De Linea Sinuum & Cycloide; by Pascal, alias Dettonville; by Des Cartes himself Vol. 3. of Letters, who saith, that by it he squared the Cycloid, and lately by the excellent Siuius, &c. 2. To remove the other prejudice that may be against this Author as defective: for the 5th Book Cylindricorum & Annularium (now printed with the rest) the Prefacer asserts to be first extant in 1659. And because we presume, the rest of these Books are already known and common, and that this hath not formerly been expos'd to sale in England; and because also it supplies and compensates those defects, we think fit to acquaint the Reader with the Argument thereof. The Author divides this Fifth Book into six parts:
1. In the first he demonstrates (in 6 Lemma's and 9 Propositions) That, if any Plain Surface have allocation about its Axis in any Situation whatsoever, and at any distance whatsoever, or none, it produceth a Round Solid equal to an Upright Solid, whole Base is the begetting Figure, and Height is equal to the Circumference described by its Center of Gravity. (This Universal Rule was invented by Guldin, and is the Basis of most of his Doctrine; but be could not demonstrate the same, though 'twas much desired.)
2. In like manner, If any Perimeter have a Rotation about its Axis in any Situation whatsoever, it begets a round Surface, equal to aright Surface, made by the same Perimeter as a Base (which may be evolv'd and made a Plain Surface) whole height is the way of circumference described by its Center of Gravity. This by 5 Lemma's and 10 Propositions.
These being two admirable Universal Rules in Geometry, the Reader will find the same (with many others) demonstrated by Dr. Wallis in his Treatise De Calculo Centr Gravitatis, which together with his other Tracts, De Motu, Statica, Mechanica, are now at the Press in London. The same Rules are likewise demonstrated in Geometriæ parte Universali Jacobi Gregorii Scoti, Patavii 1668. Of which a competent number of Copier is expected here.
The Methods of these Learned Mon are different, and good Arguments might be given, that they have not communicated nor seen the Works of each other.
Guldinus, l. 1. c. 12. shews a Mechanick way to find the Center of Gravity of a Surface or Curv'd Line, by 2 free suspensions, from the points of which, perpendiculars being drown, do cross each other at the Center of Gravity. This we mention, to keep the Reader from taking the Center of Gravity of a Curv'd Line as such (which is intended in this 2d Rule) to be the same with the Center of Gravity of the Figure thereby terminated in the first Rule.
3. Considers the Affections of Round Solids, begot from a Parabola, in 10 Propositions from Numb. 20. to 29. both inclusive; whereof the 21 and 23 gives the Hoof required by Angeli, which was formerly cubed by Greg. de S. Vincentio. In the 27th Prop. he gives the Proportion of the Parabolical Conoid to the Spindle made of the same Parabola by rotation about its Base, to be, As the Base of the Parabola is to 16/15 of the Axis; shewing, that Guldinus err'd through forgetfulness. In Prop. 29. he delivers, that the Parabola bears such a proportion to a Circle describ'd about the Base thereof as a Diameter, As the Axis of the Parabola doth to that Circumference of a Circle, whose Radius is equal to the distance of the Center of Gravity of the Semi-Parabola from the Axis.
4. Contains divers endeavors and manifold new ways towards the obtaining the Quadrature of the Circle in 12 Propositions.
5. Contains 10 Propositions, from 41 to 51; on the 42th whereof he finds a Sphere equal to an Hyperbolical Ring-solid; whence divers ways are open'd towards the attaining the Quadrature of the Hyperbola: And he finds at Sphere equal to a Ring made by the Rotation of a Segment of an Hyperbola, and of the Segment of a Circle thereto annexed, dcscribed about the Base of the Hyperbola as a Chord Line: Then he absolutely cubes certain Hoofs cut out of an Hyperbolical Cylinder, and thence derives other ways towards the obtaining the Quadrature of the Hyperbola.
6. Delivers; Theorems, shewing the proportion between an Hyperbola and a Circle: which are conceived to be wholly new.
But these Theorems suppose the Quadrature of both Figures known, viz. That of a Circle, in requiring the length of the Circumference of a Circle, described by the Center of Gravity of an Hyperbola; which Center cannot be found, without giving the Quadrature or Area of the Hyperbola: which hath been most happily perform'd by M. Mercator in his Logaritimo-Technia and further advanc'd by Dr. Wallis in N. 38. of these Transactions; and by M. Gregorii also further promoted and otherwise perform'd in his Exercitationes Geometricæ, where he shews, the same Methods and Approaches to be likewise applicable to the Circle.
What we have said, being an Account of one of the most considerable Volumes of Mathematicks extant, we hope we may be the better excused for prolixity. This Author formerly publish'd the Elements of Plain and Solid Geometry in 8°, and an Arithmetick in 8°, wherein a promised a Treatise of Algebra.
Errat P, 265. l. 24. r.m PC; p. 866. l. 3. del. sinistrorsum; ibid. l. 18. r. Gravitationem; ib. l. 24 .r, progressivo; ib. l. 29. r. fit 5, p. 867. l. 23. r. improprie.
👉 P. 863. Insert immediately before these words [Lege syllabas, Regula. Re, Se, faciunt oR, oS : Ro, So faciunt eS, eR.
In the SAVOY Printed by T.N. for John Martyn, Printer to the Royal Society, and are to be sold at the Bell a little without Temple-Bar, 1668.