1911 Encyclopædia Britannica/Arithmetic
ARITHMETIC (Gr. ἀριθμητική, sc. τέχνη, the art of counting, from ἀριθμός, number), the art of dealing with numerical quantities in their numerical relations.
1. Arithmetic is usually divided into Abstract Arithmetic and Concrete Arithmetic, the former dealing with numbers and the latter with concrete objects. This distinction, however, might be misleading. In stating that the sum of 11d. and 9d. is 1s. 8d. we do not mean that nine pennies when added to eleven pennies produce a shilling and eight pennies. The sum of money corresponding to 11d. may in fact be made up of coins in several different ways, so that the symbol “11d.” cannot be taken as denoting any definite concrete objects. The arithmetical fact is that 11 and 9 may be regrouped as 12 and 8, and the statement “11d. + 9d. = 1s. 8d.” is only an arithmetical statement in so far as each of the three expressions denotes a numerical quantity (§ 11).
2. The various stages in the study of arithmetic may be arranged in different ways, and the arrangement adopted must be influenced by the purpose in view. There are three main purposes, the practical, the educational, and the scientific; i.e. the subject may be studied with a view to technical skill in dealing with the arithmetical problems that arise in actual life, or for the sake of its general influence on mental development, or as an elementary stage in mathematical study.
3. The practical aspect is an important one. The daily activities of the great mass of the adult population, in countries where commodities are sold at definite prices for definite quantities, include calculations which have often to be performed rapidly, on data orally given, and leading in general to results which can only be approximate; and almost every branch of manufacture or commerce has its own range of applications of arithmetic. Arithmetic as a school subject has been largely regarded from this point of view.
4. From the educational point of view, the value of arithmetic has usually been regarded as consisting in the stress it lays on accuracy. This aspect of the matter, however, belongs mainly to the period when arithmetic was studied almost entirely for commercial purposes; and even then accuracy was not found always to harmonize with actuality. The development of physical science has tended to emphasize an exactly opposite aspect, viz. the impossibility, outside a certain limited range of subjects, of ever obtaining absolute accuracy, and the consequent importance of not wasting time in attempting to obtain results beyond a certain degree of approximation.
5. As a branch of mathematics, arithmetic may be treated logically, psychologically, or historically. All these aspects are of importance to the teacher: the logical, in order that he may know the end which he seeks to attain; the psychological, that he may know how best to attain this end; and the historical, for the light that history throws on psychology,
The logical arrangement of the subject is not the best for elementary study. The division into abstract and concrete, for instance, is logical, if the former is taken as relating to number and the latter to numerical quantity (§ 11). But the result of a rigid application of this principle would be that the calculation of the cost of 3 ℔ of tea at 2s. a ℔ would be deferred until after the study of logarithms. The psychological treatment recognizes the fact that the concrete precedes the abstract and that the abstract is based on the concrete; and it also recognizes the futility of attempting a strictly continuous development of the subject.
On the other hand, logical analysis is necessary if the subject is to be understood. As an illustration, we may take the elementary processes of addition, subtraction, multiplication and division. These are still called in text-books the “four simple rules”; but this name ignores certain essential differences. (i) If we consider that we are dealing with numerical quantities, we must recognize the fact that, while addition and subtraction might in the first instance be limited to such quantities, multiplication and division necessarily introduce the idea of pure number. (ii) If on the other hand we regard ourselves as dealing with pure number throughout, then, as multiplication is continued addition, we ought to include in our classification involution as continued multiplication. Or we might say that, since multiplication is a form of addition, and division a form of subtraction, there are really only two fundamental processes, viz. addition and subtraction. (iii) The inclusion of the four processes under one general head fails to indicate the essential difference between addition and multiplication, as direct processes, on the one hand, and subtraction and division, as inverse processes, on the other (§ 59).
6. The present article deals mainly with the principles of the subject, for which a logical arrangement is on the whole the more convenient. It is not suggested that this is the proper order to be adopted by the teacher.
I. Number
7. Ordinal and Cardinal Numbers.—One of the primary distinctions in the use of number is between ordinal and cardinal numbers, or rather between the ordinal and the cardinal aspects of number. The usual statement is that one, two, three, ... are cardinal numbers, and first, second, third, ... are ordinal numbers. This, however, is an incomplete statement; the words one, two, three, ... and the corresponding symbols 1, 2, 3, ... or I, II, III, ... are used sometimes as ordinals, i.e. to denote the place of an individual in a series, and sometimes as cardinals, i.e. to denote the total number since the commencement of the series.
On the whole, the ordinal use is perhaps the more common. Thus “100” on a page of a book does not mean that the page is 100 times the page numbered 1, but merely that it is the page after 99. Even in commercial transactions, in dealing with sums of money, the statement of an amount often has reference to the last item added rather than to a total; and geometrical measurements are practically ordinal (§ 26).
For ordinal purposes we use, as symbols, not only figures, such as 1, 2, 3, ... but also letters, as a, b, c, ... Thus the pages of a book may be numbered 1, 2, 3, ... and the chapters I, II, III, ... but the sheets are lettered A, B, C, ... Figures and letters may even be used in combination; thus 16 may be followed by 16a and 16b, and these by 17, and in such a case the ordinal 100 does not correspond with the total (cardinal) number up to this point.
Arithmetic is supposed to deal with cardinal, not with ordinal numbers; but it will be found that actual numeration, beyond about three or four, is based on the ordinal aspect of number, and that a scientific treatment of the subject usually requires a return to this fundamental basis.
One difference between the treatment of ordinal and of cardinal numbers may be noted. Where a number is expressed in terms of various denominations, a cardinal number usually begins with the largest denomination, and an ordinal number with the smallest. Thus we speak of one thousand eight hundred and seventy-six, and represent it by MDCCCLXXVI or 1876; but we should speak of the third day of August 1876, and represent it by 3. 8. 1876. It might appear as if the writing of 1876 was an exception to this rule; but in reality 1876, when used in this way, is partly cardinal and partly ordinal, the first three figures being cardinal and the last ordinal. To make the year completely ordinal, we should have to describe it as the 6th year of the 8th decade of the 9th century of the 2nd millennium; i.e. we should represent the date by 3. 8. 6. 8. 9. 2, the total number of years, months and days completed being 1875. 7. 2. In using an ordinal we direct our attention to a term of a series, while in using a cardinal we direct our attention to the interval between two terms. The total number in the series is the sum of the two cardinal numbers obtained by counting up to any interval from the beginning and from the end respectively; but if we take the ordinal numbers from the beginning and from the end we count one term twice over. Hence, if there are 365 days in a year, the 100th day from the beginning is the 266th, not the 265th, from the end.
8. Meaning of Names of Numbers.—What do we mean by any particular number, e.g. by seven, or by two hundred and fifty-three? We can define two as one and one, and three as one and one and one; but we obviously cannot continue this method for ever. For the definition of large numbers we may employ either of two methods, which will be called the grouping method and the counting method.
(i) Method of Grouping.—The first method consists in defining the first few numbers, and forming larger numbers by groups or aggregates, formed partly by multiplication and partly by addition. Thus, on the denary system (§16) we can give independent definitions to the numbers up to ten, and then regard (e.g.) fifty-three as a composite number made up of five tens and three ones. Or, on the quinary-binary system, we need only give independent definitions to the numbers up to five; the numbers six, seven, . . . can then be regarded as five and one, five and two, . . ., a fresh series being started when we get to five and five or ten. The grouping method introduces multiplication into the definition of large numbers; but this, from the teacher’s point of view, is not now such a serious objection as it was in the days when children were introduced to millions and billions before they had any idea of elementary arithmetical processes.
(ii) Method of Counting.—The second method consists in taking a series of names or symbols for the first few numbers, and then repeating these according to a regular system for successive numbers, so that each number is defined by reference to the number immediately preceding it in the series. Thus two still means one and one, but three means two and one, not one and one and one. Similarly two hundred and fifty-three does not mean two hundreds, five tens and three ones, but one more than two hundred and fifty-two; and the number which is called one hundred is not defined as ten tens, but as one more than ninety-nine.
9. Concrete and Abstract Numbers.—Number is concrete or abstract according as it does or does not relate to particular objects. On the whole, the grouping method refers mainly to concrete numbers and the counting method to abstract numbers. If we sort objects into groups of ten, and find that there are five groups of ten with three over, we regard the five and the three as names for the actual sets of groups or of individuals. The three, for instance, are regarded as a whole when we name them three. If, however, we count these three as one, two, three, then the number of times we count is an abstract number. Thus number in the abstract is the number of times that the act of counting is performed in any particular case. This, however, is a description, not a definition, and we still want a definition for “number” in the phrase “number of times.”
10. Definition of “Number.”—Suppose we fix on a certain sequence of names “one,” “two,” “three,” . . ., or symbols such as 1, 2, 3, ...; this sequence being always the same. If we take a set of concrete objects, and name them in succession “one,” “two,” “three,” . . ., naming each once and once only, we shall not get beyond a certain name, e.g. “six.” Then, in saying that the number of objects is six, what we mean is that the name of the last object named is six. We therefore only require a definite law for the formation of the successive names or symbols. The symbols 1, 2, . . . 9, 10, . . ., for instance, are formed according to a definite law; and in giving 253 as the number of a set of objects we mean that if we attach to them the symbols 1, 2, 3, . . . in succession, according to this law, the symbol attached to the last object will be 253. If we say that this act of attaching a symbol has been performed 253 times, then 253 is an abstract (or pure) number.
Underlying this definition is a certain assumption, viz. that if we take the objects in a different order, the last symbol attached will still be 253. This, in an elementary treatment of the subject, must be regarded as axiomatic; but it is really a simple case of mathematical induction. (See Algebra.) If we take two objects A and B, it is obvious that whether we take them as A, B, or as B, A, we shall in each case get the sequence 1, 2. Suppose this were true for, say, eight objects, marked 1 to 8. Then, if we introduce another object anywhere in the series, all those coming after it will be displaced so that each will have the mark formerly attached to the next following; and the last will therefore be 9 instead of 8. This is true, whatever the arrangement of the original objects may be, and wherever the new one is introduced; and therefore, if the theorem is true for 8, it is true for 9. But it is true for 2; therefore it is true for 3; therefore for 4, and so on.
11. Numerical Quantities.—If the term number is confined to number in the abstract, then number in the concrete may be described as numerical quantity. Thus £3 denotes £1 taken 3 times. The £1 is termed the unit. A numerical quantity, therefore, represents a certain unit, taken a certain number of times. If we take £3 twice, we get £6; and if we take 3s. twice, we get 6s., i.e. 6 times 1s. Thus arithmetical processes deal with numerical quantities by dealing with numbers, provided the unit is the same throughout. If we retain the unit, the arithmetic is concrete; if we ignore it, the arithmetic is abstract. But in the latter case it must always be understood that there is some unit concerned, and the results have no meaning until the unit is reintroduced.
II. Notation, Numeration and Number-Ideation
12. Terms used.—The representation of numbers by spoken sounds is called numeration; their representation by written signs is called notation. The systems adopted for numeration and for notation do not always agree with one another; nor do they always correspond with the idea which the numbers subjectively present. This latter presentation may, in the absence of any accepted term, be called number-ideation; this word covering not only the perception or recognition of particular numbers, but also the formation of a number-concept.
13. Notation of Numbers.—The system which is now almost universally in use amongst civilized nations for representing cardinal numbers is the Hindu, sometimes incorrectly called the Arabic, system. The essential features which distinguish this from other systems are (1) the limitation of the number of different symbols, only ten being used, however large the number to be represented may be; (2) the use of the zero to indicate the absence of number; and (3) the principle of local value, by which a symbol in effect represents different numbers, according to its position. The symbols denoting a number are called its digits.
A brief account of the development of the system will be found under Numeral. Here we are concerned with the principle, the explanation of which is different according as we proceed on the grouping or the counting system.
(i) On the grouping system we may in the first instance consider that we have separate symbols for numbers from “one” to “nine,” but that when we reach ten objects we put them in a group and denote this group by the symbol used for “one,” but printed in a different type or written of a different size or (in teaching) of a different colour. Similarly when we get to ten tens we denote them by a new representation of the figure denoting one. Thus we may have:
| ones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| tens | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| hundreds, | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| &c. | &c. | &c. |
(ii) On the counting system we may consider that we have a series of objects (represented in the adjoining diagram by dots), and that we attach to these objects in succession the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, repeating this series indefinitely. There is as yet no distinction between the first object marked 1 and the second object marked 1. We can, however, attach to the 0’s the same symbols, 1, 2, . . . 0 in succession, in a separate column, repeating the series indefinitely; then do the same with every 0 of this new series; and so on. Any particular object is then defined completely by the combination of the symbols last written down in each series; and this combination of symbols can equally be used to denote the number of objects up to and including the last one (§ 10).
In writing down a number in excess of 1000 it is (except where the number represents a particular year) usual in England and America to group the figures in sets of three, starting from the right, and to mark off the sets by commas. On the continent of Europe the figures are taken in sets of three, but are merely spaced, the comma being used at the end of a number to denote the commencement of a decimal.
The zero, called “nought,” is of course a different thing from the letter O of the alphabet, but there may be a historical connexion between them (§ 79). It is perhaps interesting to note that the latter-day telephone operator calls 1907 “nineteen O seven” instead of “nineteen nought seven.”
14. Direction of the Number-Series.—There is no settled convention as to the direction in which the series of symbols denoting the successive numbers one, two, three, . . . is to be written.
(i) If the numbers were written down in succession, they would naturally proceed from left to right, thus:—1, 2, 3, . . .... This system, however, would require that in passing to “double figures” the figure denoting tens should be written either above or below the figure denoting ones, e.g.
| 1 | ||||
| 1, 2, . . . 8, 9, | 0, 1, 2, . . . or 1, 2, . . . , 8, 9, | 0, 1, 2, . . . | ||
| 1 |
The placing of the tens-figure to the left of the ones-figure will not seem natural unless the number-series runs either up or down.
(ii) In writing down any particular number, the successive powers of ten are written from right to left, e.g. 5,462,198 is
| (6) | (5) | (4) | (3) | (2) | (1) | (0) |
| 5 | 4 | 6 | 2 | 1 | 9 | 8 |
the small figures in brackets indicating the successive powers. On the other hand, in writing decimals, the sequence (of negative powers) is from left to right.
(iii) In making out lists, schedules, mathematical tables (e.g. a multiplication-table), statistical tables, &c., the numbers are written vertically downwards. In the case of lists and schedules the numbers are only ordinals; but in the case of mathematical or statistical tables they are usually regarded as cardinals, though, when they represent values of a continuous quantity, they must be regarded as ordinals (§§ 26, 93).
(iv) In graphic representation measurements are usually made upwards; the adoption of this direction resting on certain deeply rooted ideas (§ 23).
This question of direction is of importance in reference to the development of useful number-forms (§ 23); and the existence of the two methods mentioned under (iii) and (iv) above produces confusion in comparing numerical tabulation with graphical representation. It is generally accepted that the horizontal direction of increase, where a horizontal direction is necessary, should be from left to right; but uniformity as regards vertical direction could only be attained either by printing mathematical tables upwards or by taking “downwards,” instead of “upwards,” as the “positive” direction for graphical purposes. The downwards direction will be taken in this article as the normal one for succession of numbers (e.g. in multiplication), and, where the arrangement is horizontal, it is to be understood that this is for convenience of printing. It should be noticed that, in writing the components of a number 253 as 200, 50 and 3, each component beneath the next larger one, we are really adopting the downwards principle, since the figures which make up 253 will on this principle be successively 2, 5 and 3 (§ 13 (ii)).
| 200 |
| 50 |
| 3 |
| —— |
| 253 |
15. Roman Numerals.—Although the Roman numerals are no longer in use for representing cardinal numbers, except in certain special cases (e.g. clock-faces, milestones and chemists’ prescriptions), they are still used for ordinals.
The system differs completely from the Hindu system. There are no single symbols for two, three, &c.; but numbers are represented by combinations of symbols for one, five, ten, fifty, one hundred, five hundred, &c., the numbers which have single symbols, viz. I, V, X, L, C, D, M, proceeding by multiples of five and two alternately. Thus 1878 is MDCCCLXXVIII, i.e. thousand five-hundred hundred hundred hundred fifty ten ten five one one one.
The system is therefore essentially a cardinal and grouping one, i.e. it represents a number as the sum of sets of other numbers. It is therefore remarkable that it should now only be used for ordinal purposes, while the Hindu system, which is ordinal in its nature, since a single series is constantly repeated, is used almost exclusively for cardinal numbers. This fact seems to illustrate the truth that the counting principle is the fundamental one, to which the interpretation of grouped numbers must ultimately be referred.
The normal process of writing the larger numbers on the left is in certain cases modified in the Roman system by writing a number in front of a larger one to denote subtraction. Thus four, originally written IIII, was later written IV. This may have been due to one or both of two causes; a primitive tendency to refer numbers, in numeration, to the nearest large number (§ 24 (iv)), and the difficulty of perceiving the number of a group of objects beyond about three (§ 22). Similarly IX, XL and XC were written for nine, forty and ninety respectively. These, however, were later developments.
16. Scales of Notation.—In the Hindu system the numbering proceeds by tens, tens of tens, &c.; thus the figure in the fifth place, counting from the right, denotes the product of the corresponding number by four tens in succession. The notation is then said to be in the scale of which ten is the base, or in the denary scale. The Roman system, except for the use of symbols for five, fifty, &c., is also in the denary scale, though expressed in a different way. The introduction of these other symbols produces a compound scale, which may be called a quinary-binary, or, less correctly, a quinary-denary scale.
The figures used in the Hindu notation might be used to express numbers in any other scale than the denary, provided new symbols were introduced if the base of the scale exceeded ten. Thus 1878 in the quinary-binary scale would be 1131213, and 1828 would be 1130213; the meaning of these is seen at once by comparison with MDCCCLXXVIII and MDCCCXXVIII. Similarly the number which in the denary scale is 215 would in the quaternary scale (base 4) be 3113, being equal to 3·4·4·4 + 1·4·4 + 1·4 + 3.
The use of the denary scale in notation is due to its use in numeration (§ 18); this again being due (as exemplified by the use of the word digit) to the primitive use of the fingers for counting. If mankind had had six fingers on each hand and six toes on each foot, we should be using a duodenary scale (base twelve), which would have been far more convenient.
17. Notation of Numerical Quantities.—Over a large part of the civilized world the introduction of the metric system (§ 118) has caused the notation of all numerical quantities to be in the denary scale. In Great Britain and her colonies, however, and in the United States, other systems of notation still survive, though there is none which is consistently in one scale, other than the denary. The method is to form quantities into groups, and these again into larger groups; but the number of groups making one of the next largest groups varies as we proceed along the scale. The successive groups or units thus formed are called denominations. Thus twelve pennies make a shilling, and twenty shillings a pound, while the penny is itself divided into four farthings (or two halfpennies). There are, therefore, four denominations, the bases for conversion of one denomination into the next being successively four (or two), twelve and twenty. Within each denomination, however, the denary notation is employed exclusively, e.g. “twelve shillings” is denoted by 12s.
The diversity of scales appears to be due mainly to four causes: (i) the tendency to group into scores (§ 20); (ii) the tendency to subdivide into twelve; (iii) the tendency to subdivide into two or four, with repetitions, making subdivision into sixteen or sixty-four; and (iv) the independent adoption of different units for measuring the same kind of magnitude.
Where there is a division into sixteen parts, a binary scale may be formed by dividing into groups of two, four or eight. Thus the weights ordinarily in use for measuring from 14 oz. up to 2 ℔ give the basis for a binary scale up to not more than eight figures, only 0 and 1 being used. The points of the compass might similarly be expressed by numbers in a binary scale; but the numbers would be ordinal, and the expressions would be analogous to those of decimals rather than to those of whole numbers.
In order to apply arithmetical processes to a quantity expressed in two or more denominations, we must first express it in terms of a single denomination by means of a varying scale of notation. Thus £254, 13S. 6d. may be written £254 13S. 6d.; each of the numbers in brackets indicating the number of units in one denomination that go to form a unit in the next higher denomination. To express the quantity in terms of £, it ought to be written £254 13 6; this would mean £254 1361220 or £(254 + 1320 + 620·12), and therefore would involve a fractional number.
A quantity expressed in two or more denominations is usually called a compound number or compound quantity. The former term is obviously incorrect, since a quantity is not a number; and the latter is not very suggestive. For agreement with the terminology of fractional numbers (§ 62) we shall describe such a quantity as a mixed quantity. The letters or symbols descriptive of each denomination are visually placed after or (in actual calculations) above the figures denoting the numbers of the corresponding units; but in a few cases, e.g. in the case of £, the symbol is placed before the figures. There would be great convenience in a general adoption of this latter method; the combination of the two methods in such an expression as £123, 16s. 412d. is especially awkward.
18. Numeration.—The names of numbers are almost wholly based on the denary scale; thus eighteen means eight and ten, and twenty-four means twice ten and four. The words eleven and twelve have been supposed to suggest etymologically a denary basis (see, however, Numeral).
Two exceptions, however, may be noted.
(i) The use of dozen, gross (= dozen dozen), and great gross (= dozen gross) indicates an attempt at a duodenary basis. But the system has never spread; and the word “dozen” itself is based on the denary scale.
(ii) The score (twenty) has been used as a basis, but to an even more limited extent. There is no essential difference, however, between this and the denary basis. As the latter is due to finger-reckoning, so the use of the fingers and the toes produced a vigesimal scale. Examples of this are given in § 20; it is worthy of notice that the vigesimal (or, rather, quinary-quaternary) system was used by the Mayas of Yucatan, and also, in a more perfect form, by the Nahuatl (Aztecs) of Mexico.
The number ten having been taken as the basis of numeration, there are various methods that might consistently be adopted for naming large numbers.
(i) We might merely name the figures contained in the number. This method is often adopted in practical life, even as regards mixed quantities; thus £57,593, 16s. 4d. would be read as five seven, five nine three, sixteen and four pence.
(ii) The word ten might be introduced, e.g. 593 would be five ten ten ninety (= nine ten) and three.
(iii) Names might be given to the successive powers of ten, up to the point to which numeration of ones is likely to go. Partial applications of this method are found in many languages.
(iv) A compromise between the last two methods would be to have names for the series of numbers, beginning with ten, each of which is the “square” of the preceding one. This would in effect be analysing numbers into components of the form a. 10b where a is less than 10, and the index b is expressed in the binary scale, e.g. 7,000,000 would be 7.104.102, and 700,000 would be 7.104.101.
The British method is a mixture of the last two, but with an index-scale which is partly ternary and partly binary. There are separate names for ten, ten times ten (= hundred), and ten times ten times ten (= thousand); but the next single name is million, representing a thousand times a thousand. The next name is billion, which in Great Britain properly means a million million, and in the United States (as in France) a thousand million.
19. Discrepancies between Numeration and Notation.—Although numeration and notation are both ostensibly on the denary system, they are not always exactly parallel. The following are a few of the discrepancies.
(i) A set of written symbols is sometimes read in more than one way, while on the other hand two different sets of symbols (at any rate if denoting numerical quantities) may be read in the same way. Thus 1820 might be read as one thousand eight hundred and twenty if it represented a number of men, but it would be read as eighteen hundred and twenty if it represented a year of the Christian era; while 1s. 6d. and 18d. might both be read as eighteenpence. As regards the first of these two examples, however, it would be more correct to write 1,820 for the former of the two meanings (cf. § 13).
(ii) The symbols 11 and 12 are read as eleven and twelve, not (except in elementary teaching) as ten-one and ten-two.
(iii) The names of the numbers next following these, up to 19 inclusive, only faintly suggest a ten. This difficulty is not always recognized by teachers, who forget that they themselves had to be told that eighteen means eight-and-ten.
(iv) Even beyond twenty, up to a hundred, the word ten is not used in numeration, e.g. we say thirty-four, not three ten four.
(v) The rule that the greater number comes first is not universally observed in numeration. It is not observed, for instance, in the names of numbers from 13 to 19; nor was it in the names from which eleven and twelve are derived. Beyond twenty it is usually, but not always, observed; we sometimes instead of twenty-four say four and twenty. (This latter is the universal system in German, up to 100, and for any portion of 100 in numbers beyond 100.)
20. Other Methods of Numeration and Notation.—It is only possible here to make a brief mention of systems other than those now ordinarily in use.
(i) Vigesimal Scale.—The system of counting by twenties instead of by tens has existed in many countries; and, though there is no corresponding notation, it still exhibits itself in the names of numbers. This is the case, for instance, in the Celtic languages; and the Breton or Gaulish names have affected the Latin system, so that the French names for some numbers are on the vigesimal system. This system also appears in the Danish numerals. In English the use of the word score to represent twenty—e.g. in “threescore and ten” for seventy—is superimposed on the denary system, and has never formed an essential part of the language. The word, like dozen and couple, is still in use, but rather in a vague than in a precise sense.
(ii) Roman System.—The Roman notation has been explained above (§ 15). Though convenient for exhibiting the composition of any particular number, it was inconvenient for purposes of calculation; and in fact calculation was entirely (or almost entirely) performed by means of the abacus (q.v.). The numeration was in the denary scale, so that it did not agree absolutely with the notation. The principle of subtraction from a higher number, which appeared in notation, also appeared in numeration, but not for exactly the same numbers or in exactly the same way; thus XVIII was two-from-twenty, and the next number was one-from-twenty, but it was written XIX, not IXX.
(iii) Other Systems of Antiquity.—The Egyptian notation was purely denary, the only separate signs being those for 1, 10, 100, &c. The ordinary notation of the Babylonians was denary, but they also used a sexagesimal scale, i.e. a scale whose base was 60. The Hebrews had a notation containing separate signs (the letters of the alphabet) for numbers from 1 to 10, then for multiples of 10 up to 100, and then for multiples of 100 up to 400, and later up to 1000.
The earliest Greek system of notation was similar to the Roman, except that the symbols for 50, 500, &c., were more complicated. Later, a system similar to the Hebrew was adopted, and extended by reproducing the first nine symbols of the series, preceded by accents, to denote multiplication by 1000.
On the island of Ceylon there still exists, or existed till recently, a system which combines some of the characteristics of the later Greek (or Semitic) and the modern European notation; and it is conjectured that this was the original Hindu system.
For a further account of the above systems see Numeral, and the authorities quoted at the end of the present article.
21. The Number-Concept.—It is probable that very few people have any definite mental presentation of individual numbers (i.e. numbers proceeding by differences of one) beyond 100, or at any rate beyond 144. Larger numbers are grasped by forming numbers into groups or by treating some large number as a unit. A person would appreciate the difference between 93,000,000 m. and 94,000,000 m. as the distance of the centre of the sun from the centre of the earth at a particular moment; but he certainly would not appreciate the relative difference between 93,000,000 m. and 93,000,001 m. In order to get an idea of 93,000,000, he must take a million as his unit. Similarly, in the metric system he cannot mentally compare two units, one of which is 1000 times the other. The metre and the kilometre, for instance, or the metre and the millimetre, are not directly comparable; but the metre can be conceived as containing 100 centimetres.
On the other hand, it would seem that, for most educated people, sixteen and seventeen or twenty-six and twenty-seven, and even eighty-six and eighty-seven, are single numbers, just as six and seven are, and are not made up of groups of tens and ones. In other words, the denary scale, though adopted in notation and in numeration, does not arise in the corresponding mental concept until we get beyond 100.
Again, in the use of decimals, it is unusual to give less than two figures. Thus 3·142 or 3·14 would be quite intelligible; but 3·1 does not convey such a good idea to most people as either 3110 or 3·10, i.e. as an expression denoting a fraction or a percentage.
There appears therefore to be a tendency to use some larger number than ten as a basis for grouping into new units or for subdivision into parts. The Babylonians adopted 60 for both these purposes, thus giving us the sexagesimal division of angles and of time.
This view is supported, not only by the intelligibility of percentages to ordinary persons, but also by the tendency, noted above (§ 19), to group years into centuries, and to avoid the use of thousands. Thus 1876 is not 1 thousand, 8 hundred, 7 tens and 6, but 18 hundred and 76, each of the numbers 18 and 76 being named as if it were a single number. It is also in accordance with what is so far known about number-forms (§ 23).
If there is this tendency to adopt 100 as a basis instead of 10, the teaching of decimals might sometimes be simplified by proceeding from percentages to percentages of percentages, i.e. by commencing with centesimals instead of with decimals.
22. Perception of Number.—In using material objects as a basis for developing the number-concept, it must be remembered that it is only when there are a few objects that their number can be perceived without either counting or the performance of some arithmetical process such as addition. If four coins are laid on a table, close together, they can (by most adults) be seen to be four, without counting; but seven coins have to be separated mentally into two groups, the numbers of which are added, or one group has to be seen and the remaining objects counted, before the number is known to be seven.
The actual limit of the number that can be “seen”—i.e. seen without counting or adding—depends for any individual on the shape and arrangement of the objects, but under similar conditions it is not the same for all individuals. It has been suggested that as many as six objects can be seen at once; but this is probably only the case with few people, and with them only when the objects have a certain geometrical arrangement. The limit for most adults, under favourable conditions, is about four. Under certain conditions it is less; thus IIII, the old Roman notation for four, is difficult to distinguish from III, and this may have been the main reason for replacing it by IV (§ 15).
In the case of young children the limit is probably two. That this was also the limit in the case of primitive races, and that the classification of things was into one, two and many, before any definite process of counting (e.g. by the fingers) came to be adopted, is clear from the use of the “dual number” in language, and from the way in which the names for three and four are often based on those for one and two. With the individual, as with the race, the limit of the number that can be seen gradually increases up to four or five.
The statement that a number of objects can be seen to be three or four is not to be taken as implying that there is a simultaneous perception of all the objects. The attention may be directed in succession to the different objects, so that the perception is rhythmical; the distinctive rhythm thus aiding the perception of the particular number.
In consequence of this limitation of the power of perception of number, it is practically impossible to use a pure denary scale in elementary number-teaching. If a quinary-binary system (such as would naturally fit in with counting on the fingers) is not adopted, teachers unconsciously resort to a binary-quinary system. This is commonly done where cubes are used; thus seven is represented by three pairs of cubes, with a single cube at the top.
23. Visualization of the Series.—A striking fact, in reference to ideas of number, is the existence of number-forms, i.e. of definite arrangements, on an imagined plane or in space, of the mental representations of the successive numbers from 1 onwards. The proportion of persons in whom number-forms exist has been variously estimated; but there is reason to believe that the forms arise at a very early stage of childhood, and that they did at some time exist in many individuals who have afterwards forgotten them. Those persons who possess them are also apt to make spatial arrangements of days of the week or the month, months of the year, the letters of the alphabet, &c.; and it is practically certain that only children would make such arrangements of letters of the alphabet. The forms seem to result from a general tendency to visualization as an aid to memory; the letter-forms may in the first instance be quite as frequent as the number-forms, but they vanish in early childhood, being of no practical value, while the number-forms continue as an aid to arithmetical work.
The forms are varied, and have few points in common; but the following tendencies are indicated.
(i) In the majority of cases the numbers lie on a continuous (but possibly zigzag) line.
(ii) There is nearly always (at any rate in English cases) a break in direction at 12. From 1 to 12 the numbers sometimes lie in the circumference of a circle, an arrangement obviously suggested by a clock-face; in these cases the series usually mounts upwards from 12. In a large number of cases, however, the direction is steadily upwards from 1 to 12, then changing. In some cases the initial direction is from right to left or from left to right; but there are very few in which it is downwards.
(iii) The multiples of 10 are usually strongly marked; but special stress is also laid on other important numbers, e.g. the multiples of 12.
(iv) The series sometimes goes up to very high numbers, but sometimes stops at 100, or even earlier. It is not stated, in most cases, whether all the numbers within the limits of the series have definite positions, or whether there are only certain numbers which form an essential part of the figure, while others only exist potentially. Probably the latter is almost universally the case.
These forms are developed spontaneously, without suggestion from outside. The possibility of replacing them by a standard form, which could be utilized for performing arithmetical operations, is worthy of consideration; some of the difficulties in the way of standardization have already been indicated (§ 14). The general tendency to prefer an upward direction is important; and our current phraseology suggests that this is the direction which increase is naturally regarded as taking. Thus we speak of counting up to a certain number; and similarly mathematicians speak of high and ascending powers, while engineers speak of high pressure, high speed, high power, &c. This tendency is probably aided by the use of bricks or cubes in elementary number-teaching.
24. Primitive Ideas of Number.—The names of numbers give an idea of the way in which the idea of number has developed. Where civilization is at all advanced, there are usually certain names, the origin of which cannot be traced; but, as we go farther back, these become fewer, and the names are found to be composed on certain systems. The systems are varied, and it is impossible to lay down any absolute laws, but the following seem to be the main conclusions.
(i) Amongst some of the lowest tribes, as (with a few exceptions) amongst animals, the only differentiation is between one and many, or between one, two and many, or between one, two, three and many. As it becomes necessary to use higher but still small numbers, they are formed by combinations of one and two, or perhaps of three with one or two. Thus many of the Australasian and South American tribes use only one and two; seven, for instance, would be two two two one.
(ii) Beyond ten, and in many cases beyond five, the names have reference to the use of the fingers, and sometimes of the toes, for counting; and the scale may be quinary, denary or vigesimal, according as one hand, the pair of hands, or the hands and feet, are taken as the new unit. Five may be signified by the word for hand; and either ten or twenty by the word for man. Or the words signifying these numbers may have reference to the completion of some act of counting. Between five and ten; or beyond ten, the names may be due to combinations, e.g. 16 may be 10 + 5 + 1; or they may be the actual names of the fingers last counted.
(iii) There are a few, but only a few, cases in which the number 6 or 8 is named as twice 3 or twice 4; and there are also a few cases in which 7, 8 and 9 are named as 6 + 1, 6 + 2 and 6 + 3. In the large majority of cases the numbers 6, 7, 8 and 9 are 5 + 1, 5 + 2, 5 + 3 and 5 + 4, being named either directly from their composition in this way or as the fingers on the second hand.
(iv) There is a certain tendency to name 4, 9, 14 and 19 as being one short of 5, 10, 15 and 20 respectively; the principle being thus the same as that of the Roman IV, IX, &c. It is possible that at an early stage the number of the fingers on one hand or on the two hands together was only thought of vaguely as a large number in comparison with 2 or 3, and that the number did not attain definiteness until it was linked up with the smaller by insertion of the intermediate ones; and the linking up might take place in both directions.
(v) In a few cases the names of certain small numbers are the names of objects which present these numbers in some conspicuous way. Thus the word used by the Abipones to denote 5 was the name of a certain hide of five colours. It has been suggested that names of this kind may have been the origin of the numeral words of different races; but it is improbable that direct visual perception would lead to a name for a number unless a name based on a process of counting had previously been given to it.
25. Growth of the Number-Concept.—The general principle that the development of the individual follows the development of the race holds good to a certain extent in the case of the number-concept, but it is modified by the existence of language dealing with concepts which are beyond the reach of the child, and also, of course, by the direct attempts at instruction. One result is the formation of a number-series as a mere succession of names without any corresponding ideas of number; the series not being necessarily correct.
When numbering begins, the names of the successive numbers are attached to the individual objects; thus the numbers are originally ordinal, not cardinal.
The conception of number as cardinal, i.e. as something belonging to a group of objects as a whole, is a comparatively late one, and does not arise until the idea of a whole consisting of its parts has been formed. This is the quantitative aspect of number.
The development from the name-series to the quantitative conception is aided by the numbering of material objects and the performance of elementary processes of comparison, addition, &c., with them. It may also be aided, to a certain extent, by the tendency to find rhythms in sequences of sounds. This tendency is common in adults as well as in children; the strokes of a clock may, for instance, be grouped into fours, and thus eleven is represented as two fours and three. Finger-counting is of course natural to children, and leads to grouping into fives, and ultimately to an understanding of the denary system of notation.
|
Fig. 1. |
26. Representation of Geometrical Magnitude by Number.—The application of arithmetical methods to geometrical measurement presents some difficulty. In reality there is a transition from a cardinal to an ordinal system, but to an ordinal system which does not agree with the original ordinal system from which the cardinal system was derived. To see this, we may represent ordinal numbers by the ordinary numerals 1, 2, 3, ... and cardinal numbers by the Roman I, II, III, ... Then in the earliest stage each object counted is indivisible; either we are counting it as a whole, or we are not counting it at all. The symbols 1, 2, 3, ... then refer to the individual objects, as in fig. 1; this is the primary ordinal stage. Figs. 2 and 3 represent the cardinal stage; fig. 2 showing how the I, II, III, ... denote the successively larger groups of objects, while fig. 3 shows how the name II of the whole is determined by the name 2 of the last one counted.
 Fig. 2. |
 Fig. 3. |
When now we pass to geometrical measurement, each “one” is a thing which is itself divisible, and it cannot be said that at any moment we are counting it; it is only when one is completed that we can count it. The names 1, 2, 3, ... for the individual objects cease to have an intelligible meaning, and measurement is effected by the cardinal numbers I, II, III, ..., as in fig. 4. These cardinal numbers have now, however, come to denote individual points in the line of measurement, i.e. the points of separation of the individual units of length. The point III in fig. 4 does not include the point II in the same way that the number III includes the number II in fig. 2, and the points must therefore be denoted by the ordinal numbers 1, 2, 3, ... as in fig. 5, the zero 0 falling into its natural place immediately before the commencement of the first unit.
 Fig. 4. |
 Fig. 5. |
Thus, while arithmetical numbering refers to units, geometrical numbering does not refer to units but to the intervals between units.
III. Arithmetic of Integral Numbers
(i.) Preliminary
27. Equality and Identity.—There is a certain difference between the use of words referring to equality and identity in arithmetic and in algebra respectively; what is an equality in the former becoming an identity in the latter. Thus the statement that 4 times 3 is equal to 3 times 4, or, in abbreviated form, 4 × 3 = 3 × 4 (§ 28), is a statement not of identity but of equality; i.e. 4 × 3 and 3 × 4 mean different things, but the operations which they denote produce the same result. But in algebra a × b = b × a is called an identity, in the sense that it is true whatever a and b may be; while n × X = A is called an equation, as being true, when n and A are given, for one value only of X. Similarly the numbers represented by 612 and 12 are not identical, but are equal.
28. Symbols of Operation.—The failure to observe the distinction between an identity and an equality often leads to loose reasoning; and in order to prevent this it is important that definite meanings should be attached to all symbols of operation, and especially to those which represent elementary operations. The symbols − and ÷ mean respectively that the first quantity mentioned is to be reduced or divided by the second; but there is some vagueness about + and ×. In the present article a + b will mean that a is taken first, and b added to it; but a × b will mean that b is taken first, and is then multiplied by a. In the case of numbers the × may be replaced by a dot; thus 4.3 means 4 times 3. When it is necessary to write the multiplicand before the multiplier, the symbol 
will be used, so that b a will mean the same as a × b.
29. Axioms.—There are certain statements that are sometimes regarded as axiomatic; e.g. that if equals are added to equals the results are equal, or that if A is greater than B then A + X is greater than B + X. Such statements, however, are capable of logical proof, and are generalizations of results obtained empirically at an elementary stage; they therefore belong more properly to the laws of arithmetic (§ 58).
(ii.) Sums and Differences.
30. Addition and Subtraction.—Addition is the process of expressing (in numeration or notation) a whole, the parts of which have already been expressed; while, if a whole has been expressed and also a part or parts, subtraction is the process of expressing the remainder.
Except with very small numbers, addition and subtraction, on the grouping system, involve analysis and rearrangement. Thus the sum of 8 and 7 cannot be expressed as ones; we can either form the whole, and regroup it as 10 and 5, or we can split up the 7 into 2 and 5, and add the 2 to the 8 to form 10, thus getting 8 + 7 = 8 + (2 + 5) = (8 + 2) + 5 = 10 + 5 = 15. For larger numbers the rearrangement is more extensive; thus 24 + 31 = (20 + 4) + (30 + 1) = (20 + 30) + (4 + 1) = 50 + 5 = 55, the process being still more complicated when the ones together make more than ten. Similarly we cannot subtract 8 from 15, if 15 means 1 ten + 5 ones; we must either write 15 − 8 = (10 + 5) − 8 = (10 − 8) + 5 = 2 + 5 = 7, or else resolve the 15 into an inexpressible number of ones, and then subtract 8 of them, leaving 7.
Numerical quantities, to be added or subtracted, must be in the same denomination; we cannot, for instance, add 55 shillings and 100 pence, any more than we can add 3 yards and 2 metres.
31. Relative Position in the Series.—The above method of dealing with addition and subtraction is synthetic, and is appropriate to the grouping method of dealing with number. We commence with processes, and see what they lead to; and thus get an idea of sums and differences. If we adopted the counting method, we should proceed in a different way, our method being analytic.
One number is less or greater than another, according as the symbol (or ordinal) of the former comes earlier or later than that of the latter in the number-series. Thus (writing ordinals in light type, and cardinals in heavy type) 9 comes after 4, and therefore 9 is greater than 4. To find how much greater, we compare two series, in one of which we go up to 9, while in the other we stop at 4 and then recommence our counting. The series are shown below, the numbers being placed horizontally for convenience of printing, instead of vertically (§ 14):—
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 |
This exhibits 9 as the sum of 4 and 5; it being understood that the sum of 4 and 5 means that we add 5 to 4. That this gives the same result as adding 4 to 5 may be seen by reckoning the series backwards.
It is convenient to introduce the zero; thus
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 |
indicates that after getting to 4 we make a fresh start from 4 as our zero.
To subtract, we may proceed in either of two ways. The subtraction of 4 from 9 may mean either “What has to be added to 4 in order to make up a total of 9,” or “To what has 4 to be added in order to make up a total of 9.” For the former meaning we count forwards, till we get to 4, and then make a new count, parallel with the continuation of the old series, and see at what number we arrive when we get to 9. This corresponds to the concrete method, in which we have 9 objects, take away 4 of them, and recount the remainder. The alternative method is to retrace the steps of addition, i.e. to count backwards, treating 9 of one (the standard) series as corresponding with 4 of the other, and finding which number of the former corresponds with 0 of the latter. This is a more advanced method, which leads easily to the idea of negative quantities, if the subtraction is such that we have to go behind the 0 of the standard series.
32. Mixed Quantities.—The application of the above principles, and of similar principles with regard to multiplication and division, to numerical quantities expressed in any of the diverse British denominations, presents no theoretical difficulty if the successive denominations are regarded as constituting a varying scale of notation (§17). Thus the expression 2 ft. 3 in. implies that in counting inches we use 0 to eleven instead of 0 to 9 as our first repeating series, so that we put down 1 for the next denomination when we get to twelve instead of when we get to ten. Similarly 3 yds. 2 ft. means
| yds. | 0 | 1 | 2 | 3 | ||||||||
| ft. | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
The practical difficulty, of course, is that the addition of two numbers produces different results according to the scale in which we are for the moment proceeding; thus the sum of 9 and 8 is 17, 15, 13 or 11 according as we are dealing with shillings, pence, pounds (avoirdupois) or ounces. The difficulty may be minimized by using the notation explained in § 17.
(iii.) Multiples, Submultiples and Quotients.
33. Multiplication and Division are the names given to certain numerical processes which have to be performed in order to find the result of certain arithmetical operations. Each process may arise out of either of two distinct operations; but the terminology is based on the processes, not on the operations to which they belong, and the latter are not always clearly understood.
34. Repetition and Subdivision.—Multiplication occurs when a certain number or numerical quantity is treated as a unit (§ 11), and is taken a certain number of times. It therefore arises in one or other of two ways, according as the unit or the number exists first in consciousness. If pennies are arranged in groups of five, the total amounts arranged are successively once 5d., twice 5d., three times 5d., . . .; which are written 1 × 5d., 2 × 5d., 3 × 5d., . . . (§ 28). This process is repetition, and the quantities 1 × 5d., 2 × 5d., 3 × 5d., . . . are the successive multiples of 5d. If, on the other hand, we have a sum of 5s., and treat a shilling as being equivalent to twelve pence, the 5s. is equivalent to 5 × 12d.; here the multiplication arises out of a subdivision of the original unit 1s. into 12d.
Although multiplication may arise in either of these two ways, the actual process in each case is performed by commencing with the unit and taking it the necessary number of times. In the above case of subdivision, for instance, each of the 5 shillings is separately converted into pence, so that we do in fact find in succession once 12d., twice 12d., . . .; i.e. we find the multiples of 12d. up to 5 times.
The result of the multiplication is called the product of the unit by the number of times it is taken. 35. Diagram of Multiplication.—The process of multiplication is performed in order to obtain such results as the following:—
If 1 boy receives 7 apples,
then 3 boys receive 21 apples;
or
If 1s. is equivalent to 12d.,
then 5s. is equivalent to 60d.
The essential portions of these statements, from the arithmetical point of view, may be exhibited in the form of the diagrams A and B:—
or more briefly, as in C or C′ and D or D′:—
the general arrangement of the diagram being as shown in E or E′:—
Multiplication is therefore equivalent to completion of the diagram by entry of the product.
36. Multiple-Tables.—The diagram C or D of § 35 is part of a complete table giving the successive multiples of the particular unit. If we take several different units, and write down their successive multiples in parallel columns, preceded by the number-series, we obtain a multiple-table such as the following:—
| 1 | 1 | 2 | 9 | 1s. 5d. | 3 yds. 2 ft. | 17359 | . . . . . |
| 2 | 2 | 4 | 18 | 2s. 10d. | 7 yds. 1 ft. | 34718 | . . . . . |
| 3 | 3 | 6 | 27 | 4s. 3d. | 11 yds. 0 ft. | 52077 | . . . . . |
| 4 | 4 | 8 | 36 | 5s. 8d. | 14 yds. 2 ft. | 69436 | . . . . . |
| 5 | 5 | 10 | 45 | 7s. 1d. | 16 yds. 1 ft. | 86795 | . . . . . |
| . | . | . | . | . | . | . | . . . . . |
| . | . | . | . | . | . | . | . . . . . |
| . | . | . | . | . | . | . | . . . . . |
| . | . | . | . | . | . | . | . . . . . |
It is to be considered that each column may extend downwards indefinitely.
37. Successive Multiplication.—In multiplication by repetition the unit is itself usually a multiple of some other unit, i.e. it is a product which is taken as a new unit. When this new unit has been multiplied by a number, we can again take the product as a unit for the purpose of another multiplication; and so on indefinitely. Similarly where multiplication has arisen out of the subdivision of a unit into smaller units, we can again subdivide these smaller units. Thus we get successive multiplication; but it represents quite different operations according as it is due to repetition, in the sense of § 34, or to subdivision, and these operations will be exhibited by different diagrams. Of the two diagrams below, A exhibits the successive multiplication of £3 by 20, 12 and 4, and B the successive reduction of £3 to shillings, pence and farthings. The principle on which the diagrams are constructed is obvious from § 35. It should be noticed that in multiplying £3 by 20 we find the value of 20·3, but that in reducing £3 to shillings, since each £ becomes 20s., we find the value of 3·20.
38. Submultiples.—The relation of a unit to its successive multiples as shown in a multiple-table is expressed by saying that it is a submultiple of the multiples, the successive submultiples being one-half, one-third, one-fourth, . . . Thus, in the diagram of § 36, 1s. 5d. is one-half of 2s. 10d., one-third of 4s. 3d., one-fourth of 5s. 8d., . . .; these being written “12 of 2s. 10d.,” “13 of 4s. 3d.,” “14 of 5s. 8d,”. . .
The relation of submultiple is the converse of that of multiple; thus if a is 15 of b, then b is 5 times a. The determination of a submultiple is therefore equivalent to completion of the diagram E or E′ of § 35 by entry of the unit, when the number of times it is taken, and the product, are given. The operation is the converse of repetition; it is usually called partition, as representing division into a number of equal shares.
39. Quotients.—The converse of subdivision is the formation of units into groups, each constituting a larger unit; the number of the groups so formed out of a definite number of the original units is called a quotient. The determination of a quotient is equivalent to completion of the diagram by entry of the number when the unit and the product are given. There is no satisfactory name for the operation, as distinguished from partition; it is sometimes called measuring, but this implies an equality in the original units, which is not an essential feature of the operation.
40. Division.—From the commutative law for multiplication, which shows that 3 × 4d. = 4 × 3d. = 12d., it follows that the number of pence in one-fourth of 12d. is equal to the quotient when 12 pence are formed into units of 4d.; each of these numbers being said to be obtained by dividing 12 by 4. The term division is therefore used in text-books to describe the two processes described in §§ 38 and 39; the product mentioned in § 34 is the dividend, the number or the unit, whichever is given, is called the divisor, and the unit or number which is to be found is called the quotient. The symbol ÷ is used to denote both kinds of division; thus A ÷ n denotes the unit, n of which make up A, and A ÷ B denotes the number of times that B has to be taken to make up A. In the present article this confusion is avoided by writing the former as 1n of A.
Methods of division are considered later (§§ 106-108).
41. Diagrams of Division.—Since we write from left to right or downwards, it may be convenient for division to interchange the rows or the columns of the multiplication-diagram. Thus the uncompleted diagram for partition is F or G, while for measuring it is usually H; the vacant compartment being for the unit in F or G, and for the number in H. In some cases it may be convenient in measuring to show both the units, as in K.
42. Successive Division may be performed as the converse of successive multiplication. The diagrams A and B below are the converse (with a slight alteration) of the corresponding diagrams in § 37; A representing the determination of 120 of 112 of 14 of 2880 farthings, and B the conversion of 2880 farthings into £.
(iv.) Properties of Numbers.
(A) Properties not depending on the Scale of Notation.
43. Powers, Roots and Logarithms.—The standard series 1, 2, 3, . . . is obtained by successive additions of 1 to the number last found. If instead of commencing with 1 and making successive additions of 1 we commence with any number such as 3 and make successive multiplications by 3, we get a series 3, 9, 27, . . . as shown below the line in the margin. The first member of the series is 3; the second is the product of two numbers, each equal to 3; the third is the product of three numbers, each equal to 3; and so on. These are written 31 (or 3), 32, 33, 34, . . . where np denotes the product of p numbers, each equal to n. If we write np = N, then, if any two of the three numbers n, p, N are known, the third is determinate. If we know n and p, p is called the index, and n, n2, . . . np are called the first power, second power, . . . pth power of n, the series itself being called the power-series. The second power and third power are usually called the square and cube respectively. If we know p and N, n is called the pth root of N, so that n is the second (or square) root of n2, the third (or cube) root of n3, the fourth root of n4, . . . If we know n and N, then p is the logarithm of N to base n.
| 0 | 1 = 30 | n0 |
| 1 | 3 = 31 | n1 |
| 2 | 9 = 32 | n2 |
| 3 | 27 = 33 | n3 |
| 4 | 81 = 34 | n4 |
| : | : : | : |
| : | : : | : |
The calculation of powers (i.e. of N when n and p are given) is involution; the calculation of roots (i.e. of n when p and N are given) is evolution; the calculation of logarithms (i.e. of p when n and N are given) has no special name.
Involution is a direct process, consisting of successive multiplications; the other two are inverse processes. The calculation of a logarithm can be performed by successive divisions; evolution requires special methods.
The above definitions of logarithms, &c., relate to cases in which n and p are whole numbers, and are generalized later.
44. Law of Indices.—If we multiply np by nq, we multiply the product of p n’s by the product of q n’s, and the result is therefore np+q. Similarly, if we divide np by nq, where q is less than p, the result is np−q. Thus multiplication and division in the power-series correspond to addition and subtraction in the index-series, and vice versa.
If we divide np by np, the quotient is of course 1. This should be written n0. Thus we may make the power-series commence with 1, if we make the index-series commence with 0. The added terms are shown above the line in the diagram in § 43.
45. Factors, Primes and Prime Factors.—If we take the successive multiples of 2, 3, . . . as in § 36, and place each multiple opposite the same number in the original series, we get an arrangement as in the adjoining diagram. If any number N occurs in the vertical series commencing with a number n (other than 1) then n is said to be a factor of N. Thus 2, 3 and 6 are factors of 6; and 2, 3, 4, 6 and 12 are factors of 12.
| 1 | .. | .. | .. | .. | .. | .. | .. |
| 2 | 2 | .. | .. | .. | .. | .. | .. |
| 3 | .. | 3 | .. | .. | .. | .. | .. |
| 4 | 4 | .. | 4 | .. | .. | .. | .. |
| 5 | .. | .. | .. | 5 | .. | .. | .. |
| 6 | 6 | 6 | .. | .. | 6 | .. | .. |
| 7 | .. | .. | .. | .. | .. | 7 | .. |
| 8 | 8 | .. | 8 | .. | .. | .. | 8 |
| 9 | .. | 9 | .. | .. | .. | .. | .. |
| 10 | 10 | .. | .. | 10 | .. | .. | .. |
| 11 | .. | .. | .. | .. | .. | .. | .. |
| 12 | 12 | 12 | 12 | .. | 12 | .. | .. |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
A number (other than 1) which has no factor except itself is called a prime number, or, more briefly, a prime. Thus 2, 3, 5, 7 and 11 are primes, for each of these occurs twice only in the table. A number (other than 1) which is not a prime number is called a composite number.
If a number is a factor of another number, it is a factor of any multiple of that number. Hence, if a number has factors, one at least of these must be a prime. Thus 12 has 6 for a factor; but 6 is not a prime, one of its factors being 2; and therefore 2 must also be a factor of 12. Dividing 12 by 2, we get a submultiple 6, which again has a prime 2 as a factor. Thus any number which is not itself a prime is the product of several factors, each of which is a prime, e.g. 12 is the product of 2, 2 and 3. These are called prime factors.
The following are the most important properties of numbers in reference to factors:—
(i) If a number is a factor of another number, it is a factor of any multiple of that number.
(ii) If a number is a factor of two numbers, it is a factor of their sum or (if they are unequal) of their difference. (The words in brackets are inserted to avoid the difficulty, at this stage, of saying that every number is a factor of 0, though it is of course true that 0·n = 0, whatever n may be.)
(iii) A number can be resolved into prime factors in one way only, no account being taken of their relative order. Thus 12 = 2 × 2 × 3 = 2 × 3 × 2 = 3 × 2 × 2, but this is regarded as one way only. If any prime occurs more than once, it is usual to write the number of times of occurrence as an index; thus 144 = 2 × 2 × 2 × 2 × 3 × 3 = 24·32.
The number 1 is usually included amongst the primes; but, if this is done, the last paragraph requires modification, since 144 could be expressed as 1·24·32, or as 12·24·32, or as 1p·24·32, where p might be anything.
If two numbers have no factor in common (except 1) each is said to be prime to the other.
The multiples of 2 (including 1·2) are called even numbers; other numbers are odd numbers.
46. Greatest Common Divisor.—If we resolve two numbers into their prime factors, we can find their Greatest Common Divisor or Highest Common Factor (written G.C.D. or G.C.F. or H.C.F.), i.e. the greatest number which is a factor of both. Thus 144 = 24·32, and 756 = 22·33·7, and therefore the G.C.D. of 144 and 756 is 22·32 = 36. If we require the G.C.D. of two numbers, and cannot resolve them into their prime factors, we use a process described in the text-books. The process depends on (ii) of § 45, in the extended form that, if x is a factor of a and b, it is a factor of pa − qb, where p and q are any integers.
The G.C.D. of three or more numbers is found in the same way.
47. Least Common Multiple.—The Least Common Multiple, or L.C.M., of two numbers, is the least number of which they are both factors. Thus, since 144 = 24·32, and 756 = 22·33·7, the L.C.M. of 144 and 756 is 24·33·7. It is clear, from comparison with the last paragraph, that the product of the G.C.D. and the L.C.M. of two numbers is equal to the product of the numbers themselves. This gives a rule for finding the L.C.M. of two numbers. But we cannot apply it to finding the L.C.M. of three or more numbers; if we cannot resolve the numbers into their prime factors, we must find the L.C.M. of the first two, then the L.C.M. of this and the next number, and so on.
(B) Properties depending on the Scale of Notation.
48. Tests of Divisibility.—The following are the principal rules for testing whether particular numbers are factors of a given number. The number is divisible—
(i) by 10 if it ends in 0;
(ii) by 5 if it ends in 0 or 5;
(iii) by 2 if the last digit is even;
(iv) by 4 if the number made up of the last two digits is divisible by 4;
(v) by 8 if the number made up of the last three digits is divisible by 8;
(vi) by 9 if the sum of the digits is divisible by 9;
(vii) by 3 if the sum of the digits is divisible by 3; (viii) by 11 if the difference between the sum of the 1st, 3rd, 5th, . . . digits and the sum of the 2nd, 4th, 6th, . . . is zero or divisible by 11.
(ix) To find whether a number is divisible by 7, 11 or 13, arrange the number in groups of three figures, beginning from the end, treat each group as a separate number, and then find the difference between the sum of the 1st, 3rd, . . . of these numbers and the sum of the 2nd, 4th, . . . Then, if this difference is zero or is divisible by 7, 11 or 13, the original number is also so divisible; and conversely. For example, 31521 gives 521 − 31 = 490, and therefore is divisible by 7, but not by 11 or 13.
49. Casting out Nines is a process based on (vi) of the last paragraph. The remainder when a number is divided by 9 is equal to the remainder when the sum of its digits is divided by 9. Also, if the remainders when two numbers are divided by 9 are respectively a and b, the remainder when their product is divided by 9 is the same as the remainder when a·b is divided by 9. This gives a rule for testing multiplication, which is found in most text-books. It is doubtful, however, whether such a rule, giving a test which is necessarily incomplete, is of much educational value.
(v.) Relative Magnitude.
50. Fractions.—A fraction of a quantity is a submultiple, or a multiple of a submultiple, of that quantity. Thus, since 3 × 1s. 5d. = 4s. 3d., 1s. 5d. may be denoted by 13 of 4s. 3d.; and any multiple of 1s. 5d., denoted by n × 1s. 5d., may also be denoted by n3 of 4s. 3d. We therefore use “na of A” to mean that we find a quantity X such that a × X = A, and then multiply X by n.
It must be noted (i) that this is a definition of “na of,” not a definition of “na,” and (ii) that it is not necessary that n should be less than a.
51. Subdivision of Submultiple.—By 57 of A we mean 5 times the unit, 7 times which is A. If we regard this unit as being 4 times a lesser unit, then A is 7.4 times this lesser unit, and 57 of A is 5.4 times the lesser unit. Hence 57 of A is equal to 5.47.4 of A; and, conversely, 5.47.4 of A is equal to 57 of A. Similarly each of these is equal to 5.37.3 of A. Hence the value of a fraction is not altered by substituting for the numerator and denominator the corresponding numbers in any other column of a multiple-table (§ 36). If we write 5.47.4 in the form 4.54.7 we may say that the value of a fraction is not altered by multiplying or dividing the numerator and denominator by any number.
52. Fraction of a Fraction.—To find 114 of 57 of A we must convert 57 of A into 4 times some unit. This is done by the preceding paragraph. For 57 of A = 5.47.4 of A = 4.57.4 of A; i.e. it is 4 times a unit which is itself 5 times another unit, 7.4 times, which is A. Hence, taking the former unit 11 times instead of 4 times,
114 of 57 of A＝11.57.4 of A.
A fraction of a fraction is sometimes called a compound fraction.
53. Comparison, Addition and Subtraction of Fractions.—The quantities 34 of A and 57 of A are expressed in terms of different units. To compare them, or to add or subtract them, we must express them in terms of the same unit. Thus, taking 128 of A as the unit, we have (§ 51)
34 of A＝2128 of A; 57 of A＝2028 of A.
Hence the former is greater than the latter; their sum is 4128 of A; and their difference is 128 of A.
Thus the fractions must be reduced to a common denominator. This denominator must, if the fractions are in their lowest terms (§ 54), be a multiple of each of the denominators; it is usually most convenient that it should be their L.C.M. (§ 47).
54. Fraction in its Lowest Terms.—A fraction is said to be in its lowest terms when its numerator and denominator have no common factor; or to be reduced to its lowest terms when it is replaced by such a fraction. Thus 822 of A is said to be reduced to its lowest terms when it is replaced by 411 of A. It is important always to bear in mind that 411 of A is not the same as 822 of A, though it is equal to it.
55. Diagram of Fractional Relation.—To find 1024 of 14s. we have to take 10 of the units, 24 of which make up 14s. Hence the required amount will, in the multiple-table of § 36, be opposite 10 in the column in which the amount opposite 24 is 14s.; the quantity at the head of this column, representing the unit, will be found to be 7d. The elements of the multiple-table with which we are concerned are shown in the diagram in the margin. This diagram serves equally for the two statements that (i) 1024 of 14s. is 5s. 10d., (ii) 2410 of 5s. 10d. is 14s. The two statements are in fact merely different aspects of a single relation, considered in the next section.
56. Ratio.—If we omit the two upper compartments of the diagram in the last section, we obtain the diagram A. This diagram exhibits a relation between the two amounts 5s. 10d. and 14s. on the one hand, and the numbers 10 and 24 of the standard series on the other, which is expressed by saying that 5s. 10d. is to 14s. in the ratio of 10 to 24, or that 14s. is to 5s. 10d. in the ratio of 24 to 10. If we had taken 1s. 2d. instead of 7d. as the unit for the second column, we should have obtained the diagram B. Thus we must regard the ratio of a to b as being the same as the ratio of c to d, if the fractions a/b and c/d are equal. For this reason the ratio of a to b is sometimes written a/b, but the more correct method is to write it a:b.
If two quantities or numbers P and Q are to each other in the ratio of p to q, it is clear from the diagram that p times Q = q times P, so that Q = q/p of P.
57. Proportion.—If from any two columns in the table of § 36 we remove the numbers or quantities in any two rows, we get a diagram such as that here shown. The pair of compartments on either side may, as here, contain numerical quantities, or may contain numbers. But the two pairs of compartments will correspond to a single pair of numbers, e.g. 2 and 6, in the standard series, so that, denoting them by M, N and P, Q respectively, M will be to N in the same ratio that P is to Q. This is expressed by saying that M is to N as P to Q, the relation being written M:N :: P:Q; the four quantities are then said to be in proportion or to be proportionals.
This is the most general expression of the relative magnitude of two quantities; i.e. the relation expressed by proportion includes the relations expressed by multiple, submultiple, fraction and ratio.
If M and N are respectively m and n times a unit, and P and Q are respectively p and q times a unit, then the quantities are in proportion if mq = np; and conversely.
IV. Laws of Arithmetic
58. Laws of Arithmetic.—The arithmetical processes which we have considered in reference to positive integral numbers are subject to the following laws:—
(i) Equalities and Inequalities.—The following are sometimes called Axioms (§ 29), but their truth should be proved, even if at an early stage it is assumed. The symbols “>” and “<” mean respectively “is greater than” and “is less than.” The numbers represented by a, b, c, x and m are all supposed to be positive.
- (a) If a = b, and b = c, then a = c;
- (b) If a = b, then a + x = b + x, and a − x = b − x;
- (c) If a > b, then a + x > b + x, and a − x > b − x;
- (d) If a < b, then a + b < b + x, and a − x < b − x;
- (e) If a = b, then ma = mb, and a ÷ m = b ÷ m;
- (f) If a > b, then ma > mb, and a ÷ m > b ÷ m;
- (g) If a < b, then ma < mb, and a ÷ m < b ÷ m.
(ii) Associative Law for Additions and Subtractions.—This law includes the rule of signs, that a − (b − c) = a − b + c; and it states that, subject to this, successive operations of addition or subtraction may be grouped in sets in any way; e.g. a − b + c + d + e − f = a − (b − c) + (d + e − f).
(iii) Commutative Law for Additions and Subtractions, that additions and subtractions may be performed in any order; e.g. a − b + c + d = a + c − b + d = a − b + c − b.
(iv) Associative Law for Multiplications and Divisions.—This law includes a rule, similar to the rule of signs, to the effect that a ÷ (b ÷ c) = a ÷ b × c; and it states that, subject to this, successive operations of multiplication or division may be grouped in sets in any way; e.g. a ÷ b × c × d × e ÷ f = a ÷ (b ÷ c) × (d × e ÷ f).
(v) Commutative Law for Multiplications and Divisions, that multiplications and divisions may be performed in any order: e.g. a ÷ b × c × d = a × c ÷ b × d = a × d × c ÷ b.
(vi) Distributive Law, that multiplications and divisions may be distributed over additions and subtractions, e.g. that m(a + b − c) = m.a + m.b − m.c, or that (a + b − c) ÷ n = (a ÷ n) + (b ÷ n) + (c ÷ n).
In the case of (ii), (iii) and (vi), the letters a, b, c, ... may denote either numbers or numerical quantities, while m and n denote numbers; in the case of (iv) and (v) the letters denote numbers only.
59. Results of Inverse Operations.—Addition, multiplication and involution are direct processes; and, if we start with positive integers, we continue with positive integers throughout. But, in attempting the inverse processes of subtraction, division, and either evolution or determination of index, the data may be such that a process cannot be performed. We can, however, denote the result of the process by a symbol, and deal with this symbol according to the laws of arithmetic. In this way we arrive at (i) negative numbers, (ii) fractional numbers, (iii) surds, (iv) logarithms (in the ordinary sense of the word).
60. Simple Formulae.—The following are some simple formulae which follow from the laws stated in § 58.
(i) (a + b + c + ...)(p + q + r + ...) = (ap + aq + ar + ...) + (bp + bq + br + ...) + (cp + cq + cr + ...) + ...; i.e. the product of two or more numbers, each of which consists of two or more parts, is the sum of the products of each part of the one with each part of the other.
(ii) (a + b)(a − b) = a2 − b2; i.e. the product of the sum and the difference of two numbers is equal to the difference of their squares.
(iii) (a + b)2 = a2 + 2ab + b2 = a2 + (2a + b)b.
V. Negative Numbers
61. Negative Numbers may be regarded as resulting from the commutative law for addition and subtraction. According to this law, 10 + 3 + 6 − 7 = 10 + 3 − 7 + 6 = 3 + 6 − 7 + 10 = &c. But, if we write the expression as 3 − 7 + 6 + 10, this means that we must first subtract 7 from 3. This cannot be done; but the result of the subtraction, if it could be done, is something which, when 6 is added to it, becomes 3 − 7 + 6 = 3 + 6 − 7 = 2. The result of 3 − 7 is the same as that of 0 − 4; and we may write it “−4,” and call it a negative number, if by this we mean something possessing the property that −4 + 4 = 0.
This, of course, is unintelligible on the grouping system of treating number; on the counting system it merely means that we count backwards from 0, just as we might count inches backwards from a point marked 0 on a scale. It should be remembered that the counting is performed with something as unit. If this unit is A, then what we are really considering is −4A; and this means, not that A is multiplied by −4, but that A is multiplied by 4, and the product is taken negatively. It would therefore be better, in some ways, to retain the unit throughout, and to describe −4A as a negative quantity, in order to avoid confusion with the “negative numbers” with which operations are performed in formal algebra.
The positive quantity or number obtained from a negative quantity or number by omitting the “−” is called its numerical value.
VI. Fractional and Decimal Numbers
62. Fractional Numbers.—According to the definition in § 50 the quantity denoted by 36 of A is made up of a number, 3, and a unit, which is one-sixth of A. Similarly pn of A, qn of A, rn of A, ... mean quantities which are respectively p times, q times r times, ... the unit, n of which make up A. Thus any arithmetical processes which can be applied to the numbers p, q, r, ... can be applied to pn, qn, rn, ... , the denominator n remaining unaltered.
If we denote the unit 1/n of A by X, then A is n times X, and pn of n times X is p times X; i.e. pn of n times is p times.
Hence, so long as the denominator remains unaltered, we can deal with pn, qn, rn, ... exactly as if they were numbers, any operations being performed on the numerators. The expressions pn, qn, rn, ... are then fractional numbers, their relation to ordinary or integral numbers being that pn times n times is equal to p times.
This relation is of exactly the same kind as the relation of the successive digits in numbers expressed in a scale of notation whose base is n. Hence we can treat the fractional numbers which have any one denominator as constituting a number-series, as shown in the adjoining diagram. The result of taking 13 sixths of A is then seen to be the same as the result of taking twice A and one-sixth of A, so that we may regard 136 as being equal to 216. A fractional number is called a proper fraction or an improper fraction according as the numerator is or is not less than the denominator; and an expression such as 216 is called a mixed number. An improper fraction is therefore equal either to an integer or to a mixed number. It will be seen from § 17 that a mixed number corresponds with what is there called a mixed quantity. Thus £3, 17s. is a mixed quantity, being expressed in pounds and shillings; to express it in terms of pounds only we must write it £31720.
63. Fractional Numbers with different Denominators.—If we divided the unit into halves, and these new units into thirds, we should get sixths of the original unit, as shown in A; while, if we divided the unit into thirds, and these new units into halves, we should again get sixths, but as shown in B. The series of halves in the one case, and of thirds in the other, are entirely different series of fractional numbers, but we can compare them by putting each in its proper position in relation to the series of sixths. Thus 32 is equal to 96, and 53 is equal to 106, and conversely; in other words, any fractional number is equivalent to the fractional number obtained by multiplying or dividing the numerator and denominator by any integer. We can thus find fractional numbers equivalent to the sum or difference of any two fractional numbers. The process is the same as that of finding the sum or difference of 3 sixpences and 5 fourpences; we cannot subtract 3 sixpenny-bits from 5 fourpenny-bits, but we can express each as an equivalent number of pence, and then perform the subtraction. Generally, to find the sum or difference of two or more fractional numbers, we must replace them by other fractional numbers having the same denominator; it is usually most convenient to take as this denominator the L.C.M. of the original fractional numbers (cf. § 53).
64. Complex Fractions.—A fraction (or fractional number), the numerator or denominator of which is a fractional number, is called a complex fraction (or fractional number), to distinguish it from a simple fraction, which is a fraction having integers for numerator and denominator. Thus 5231113 of A means that we take a unit X such that 1113 times X is equal to A, and then take 523 times X. To simplify this, we take a new unit Y, which is 13 of X. Then A is 34 times Y, and 5231113 of A is 17 times Y, i.e. it is 12 of A.
65. Multiplication of Fractional Numbers.—To multiply 83 by 57 is to take 57 times 83. It has already been explained (§ 62) that 57 times is an operation such that 57 times 7 times is equal to 5 times. Hence we must express 83, which itself means 83 times, as being 7 times something. This is done by multiplying both numerator and denominator by 7; i.e. 83 is equal to 7.87.3, which is the same thing as 7 times 87.3. Hence 57 times 83 = 57 times 7 times 87.3 = 5 times 87.3 = 5.87.3. The rule for multiplying a fractional number by a fractional number is therefore the same as the rule for finding a fraction of a fraction.
66. Division of Fractional Numbers.—To divide 83 by 57 is to find a number (i.e. a fractional number) x such that 57 times x is equal to 83. But 75 times 57 times x is, by the last section, equal to x. Hence x is equal to 75 times 83. Thus to divide by a fractional number we must multiply by the number obtained by interchanging the numerator and the denominator, i.e. by the reciprocal of the original number.
If we divide 1 by 57 we obtain, by this rule, 75. Thus the reciprocal of a number may be defined as the number obtained by dividing 1 by it. This definition applies whether the original number is integral or fractional.
By means of the present and the preceding sections the rule given in § 63 can be extended to the statement that a fractional number is equal to the number obtained by multiplying its numerator and its denominator by any fractional number.
67. Negative Fractional Numbers.—We can obtain negative fractional numbers in the same way that we obtain negative integral numbers; thus − 57 or − 57A means that 57 or 57A is taken negatively.
68. Genesis of Fractional Numbers.—A fractional number may be regarded as the result of a measuring division (§ 39) which cannot be performed exactly. Thus we cannot divide 3 in. by 11 in. exactly, i.e. we cannot express 3 in. as an integral multiple of 11 in.; but, by extending the meaning of “times” as in § 62, we can say that 3 in. is 311 times 11 in., and therefore call 311 the quotient when 3 in. is divided by 11 in. Hence, if p and n are numbers, p/n is sometimes regarded as denoting the result of dividing p by n, whether p and n are integral or fractional (mixed numbers being included in fractional).
The idea and properties of a fractional number having been explained, we may now call it, for brevity, a fraction. Thus “23 of A” no longer means two of the units, three of which make up A; it means that A is multiplied by the fraction 23, i.e. it means the same thing as “23 times A.”
69. Percentage.—In order to deal, by way of comparison or addition or subtraction, with fractions which have different denominators, it is necessary to reduce them to a common denominator. To avoid this difficulty, in practical life, it is usual to confine our operations to fractions which have a certain standard denominator. Thus (§ 79) the Romans reckoned in twelfths, and the Babylonians in sixtieths; the former method supplied a basis for division by 2, 3, 4, 6 or 12, and the latter for division by 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, or 60. The modern method is to deal with fractions which have 100 as denominator; such fractions are called percentages. They only apply accurately to divisions by 2, 4, 5, 10, 20, 25 or 50; but they have the convenience of fitting in with the denary scale of notation, and they can be extended to other divisions by using a mixed number as numerator. One-fortieth, for instance, can be expressed as 212100, which is called 212 per cent., and usually written 212%. Similarly 313% is equal to one-thirtieth.
If the numerator is a multiple of 5, the fraction represents twentieths. This is convenient, e.g. for expressing rates in the pound; thus 15% denotes the process of taking 3s. for every £1, i.e. a rate of 3s. in the £.
In applications to money “per cent.” sometimes means “per £100.” Thus “£3, 17s. 6d. per cent.” is really the complex fraction 31761220100.
70. Decimal Notation of Percentage.—An integral percentage, i.e. a simple fraction with 100 for denominator, can be expressed by writing the two figures of the numerator (or, if there is only one figure, this figure preceded by 0) with a dot or “point” before them; thus ·76 means 76%, or 76100. If there is an integral number to be taken as well as a percentage, this number is written in front of the point; thus 23·76 × A means 23 times A, with 76% of A. We might therefore denote 76% by 0·76.
If as our unit we take X = 1100 of A = 1% of A, the above quantity might equally be written 2376 X = 2376100 of A; i.e. 23·76 × A is equal to 2376% of A.
71. Approximate Expression by Percentage.—When a fraction cannot be expressed by an integral percentage, it can be so expressed approximately, by taking the nearest integer to the numerator of an equal fraction having 100 for its denominator. Thus 17 = 1427100, so that 17 is approximately equal to 14%; and 27 = 2847)100, which is approximately equal to 29%. The difference between this approximate percentage and the true value is less than 12%, i.e. is less than 1200.
If the numerator of the fraction consists of an integer and 12—e.g. in the case of 38 = 3712100—it is uncertain whether we should take the next lowest or the next highest integer. It is best in such cases to retain the 12; thus we can write 38 = 3712% = ·3712.
72. Addition and Subtraction of Percentages.—The sum or difference of two percentages is expressed by the sum or difference of the numbers expressing the two percentages.
73. Percentage of a Percentage.—Since 37% of 1 is expressed by 0·37, 37% of 1% (i.e. of 0·01) might similarly be expressed by 0·00·37. The second point, however, is omitted, so that we write it 0·0037 or ·0037, this expression meaning 37100 of 1100 = 3710000.
On the same principle, since 37% of 45% is equal to 37100 of 45100 = 166510000 = 16100 + (65100 of 1100), we can express it by ·1665; and 3% of 2% can be expressed by ·0006. Hence, to find a percentage of a percentage, we multiply the two numbers, put 0’s in front if necessary to make up four figures (not counting fractions), and prefix the point.
74. Decimal Fractions.—The percentage-notation can be extended to any fraction which has any power of 10 for its denominator. Thus 1531000 can be written ·153 and 15300100000 can be written ·15300. These two fractions are equal to each other, and also to ·1530. A fraction written in this way is called a decimal fraction; or we might define a decimal fraction as a fraction having a power of 10 for its denominator, there being a special notation for writing such fractions.
A mixed number, the fractional part of which is a decimal fraction, is expressed by writing the integral part in front of the point, which is called the decimal point. Thus 27153010000 can be written 27·1530. This number, expressed in terms of the fraction 110000 or ·0001, would be 271530. Hence the successive figures after the decimal point have the same relation to each other and to the figures before the point as if the point did not exist. The point merely indicates the denomination in which the number is expressed: the above number, expressed in terms of 110, would be 271·530, but expressed in terms of 100 it would be ·271530.
Fractions other than decimal fractions are usually called vulgar fractions.
75. Decimal Numbers.—Instead of regarding the ·153 in 27·153 as meaning 1531000, we may regard the different figures in the expression as denoting numbers in the successive orders of submultiples of 1 on a denary scale. Thus, on the grouping system, 27·153 will mean 2·10 + 7 + 1/10 + 5/102 + 3/103, while on the counting system it will mean the result of counting through the tens to 2, then through the ones to 7, then through tenths to 1, and so on. A number made up in this way may be called a decimal number, or, more briefly, a decimal. It will be seen that the definition includes integral numbers.
76. Sums and Differences of Decimals.—To add or subtract decimals, we must reduce them to the same denomination, i.e. if one has more figures after the decimal point than the other, we must add sufficient 0’s to the latter to make the numbers of figures equal. Thus, to add 5·413 to 3·8, we must write the latter as 3·800. Or we may treat the former as the sum of 5·4 and ·013, and recombine the ·013 with the sum of 3·8 and 5·4.
77. Product of Decimals.—To multiply two decimals exactly, we multiply them as if the point were absent, and then insert it so that the number of figures after the point in the product shall be equal to the sum of the numbers of figures after the points in the original decimals.
In actual practice, however, decimals only represent approximations, and the process has to be modified (§ 111).
78. Division by Decimal.—To divide one decimal by another, we must reduce them to the same denomination, as explained in § 76, and then omit the decimal points. Thus 5·413 ÷ 3·8 = 54131000 ÷ 38001000 = 5413 ÷ 3800.
79. Historical Development of Fractions and Decimals.—The fractions used in ancient times were mainly of two kinds: unit-fractions, i.e. fractions representing aliquot parts (§ 103), and fractions with a definite denominator.
The Egyptians as a rule used only unit-fractions, other fractions being expressed as the sum of unit-fractions. The only known exception was the use of 23 as a single fraction. Except in the case of 23 and 12, the fraction was expressed by the denominator, with a special symbol above it.
The Babylonians expressed numbers less than 1 by the numerator of a fraction with denominator 60; the numerator only being written. The choice of 60 appears to have been connected with the reckoning of the year as 360 days; it is perpetuated in the present subdivision of angles.
The Greeks originally used unit-fractions, like the Egyptians; later they introduced the sexagesimal fractions of the Babylonians, extending the system to four or more successive subdivisions of the unit representing a degree. They also, but apparently still later and only occasionally, used fractions of the modern kind. In the sexagesimal system the numerators of the successive fractions (the denominators of which were the successive powers of 60) were followed by ′, ″, ‴, ⁗, the denominator not being written. This notation survives in reference to the minute (′) and second (″) of angular measurement, and has been extended, by analogy, to the foot (′) and inch (″). Since ξ represented 60, and ο was the next letter, the latter appears to have been used to denote absence of one of the fractions; but it is not clear that our present sign for zero was actually derived from this. In the case of fractions of the more general kind, the numerator was written first with ′, and then the denominator, followed by ″, was written twice. A different method was used by Diophantus, accents being omitted, and the denominator being written above and to the right of the numerator.
The Romans commonly used fractions with denominator 12; these were described as unciae (ounces), being twelfths of the as (pound).
The modern system of placing the numerator above the denominator is due to the Hindus; but the dividing line is a later invention. Various systems were tried before the present notation came to be generally accepted. Under one system, for instance, the continued sum 45+17×5+38×7×5 would be denoted by 3 1 48 7 5; this is somewhat similar in principle to a decimal notation, but with digits taken in the reverse order.
Hindu treatises on arithmetic show the use of fractions, containing a power of 10 as denominator, as early as the beginning of the 6th century A.D. There was, however, no development in the direction of decimals in the modern sense, and the Arabs, by whom the Hindu notation of integers was brought to Europe, mainly used the sexagesimal division in the ′ ″ ″′ notation. Even where the decimal notation would seem to arise naturally, as in the case of approximate extraction of a square root, the portion which might have been expressed as a decimal was converted into sexagesimal fractions. It was not until A.D. 1585 that a decimal notation was published by Simon Stevinus of Bruges. It is worthy of notice that the invention of this notation appears to have been due to practical needs, being required for the purpose of computation of compound interest. The present decimal notation, which is a development of that of Stevinus, was first used in 1617 by H. Briggs, the computer of logarithms.
80. Fractions of Concrete Quantities.—The British systems of coinage, weights, lengths, &c., afford many examples of the use of fractions. These may be divided into three classes, as follows:—
(i) The fraction of a concrete quantity may itself not exist as a concrete quantity, but be represented by a token. Thus, if we take a shilling as a unit, we may divide it into 12 or 48 smaller units; but corresponding coins are not really portions of a shilling, but objects which help us in counting. Similarly we may take the farthing as a unit, and invent smaller units, represented either by tokens or by no material objects at all. Ten marks, for instance, might be taken as equivalent to a farthing; but 13 marks are not equivalent to anything except one farthing and three out of the ten acts of counting required to arrive at another farthing.
(ii) In the second class of cases the fraction of the unit quantity is a quantity of the same kind, but cannot be determined with absolute exactness. Weights come in this class. The ounce, for instance, is one-sixteenth of the pound, but it is impossible to find 16 objects such that their weights shall be exactly equal and that the sum of their weights shall be exactly equal to the weight of the standard pound.
(iii) Finally, there are the cases of linear measurement, where it is theoretically possible to find, by geometrical methods, an exact submultiple of a given unit, but both the unit and the submultiple are not really concrete objects, but are spatial relations embodied in objects.
Of these three classes, the first is the least abstract and the last the most abstract. The first only involves number and counting. The second involves the idea of equality as a necessary characteristic of the units or subunits that are used. The third involves also the idea of continuity and therefore of unlimited subdivision. In weighing an object with ounce-weights the fact that it weighs more than 1 ℔ 3 oz. but less than 1 ℔ 4 oz. does not of itself suggest the necessity or possibility of subdivision of the ounce for purposes of greater accuracy. But in measuring a distance we may find that it is “between” two distances differing by a unit of the lowest denomination used, and a subdivision of this unit follows naturally.
VII. Approximation
81. Approximate Character of Numbers.—The numbers (integral or decimal) by which we represent the results of arithmetical operations are often only approximately correct. All numbers, for instance, which represent physical measurements, are limited in their accuracy not only by our powers of measurement but also by the accuracy of the measure we use as our unit. Also most fractions cannot be expressed exactly as decimals; and this is also the case for surds and logarithms, as well as for the numbers expressing certain ratios which arise out of geometrical relations.
Even where numbers are supposed to be exact, calculations based on them can often only be approximate. We might, for instance, calculate the exact cost of 3 ℔ 5 oz. of meat at 912 d. a ℔, but there are no coins in which we could pay this exact amount.
When the result of any arithmetical operation or operations is represented approximately but not exactly by a number, the excess (positive or negative) of this number over the number which would express the result exactly is called the error.
82. Degree of Accuracy.—There are three principal ways of expressing the degree of accuracy of any number, i.e. the extent to which it is equal to the number it is intended to represent.
(i) A number can be correct to so many places of decimals. This means (cf. § 71) that the number differs from the true value by less than one-half of the unit represented by 1 in the last place of decimals. For instance, ·143 represents 17 correct to 3 places of decimals, since it differs from it by less than ·0005. The final figure, in a case like this, is said to be corrected.
This method is not good for comparative purposes. Thus ·143 and 14·286 represent respectively 17 and 1007 to the same number of places of decimals, but the latter is obviously more exact than the former.
(ii) A number can be correct to so many significant figures. The significant figures of a number are those which commence with the first figure other than zero in the number; thus the significant figures of 13·027 and of ·00013027 are the same.
This is the usual method; but the relative accuracy of two numbers expressed to the same number of significant figures depends to a certain extent on the magnitude of the first figure. Thus ·14286 and ·85714 represent 17 and 67 correct to 5 significant figures; but the latter is relatively more accurate than the former. For the former shows only that 17 lies between ·142855 and ·142865, or, as it is better expressed, between ·1428512 and ·1428612; but the latter shows that 67 lies between ·8571312 and ·8571412, and therefore that 17 lies between ·14285712 and ·14285912.
In either of the above cases, and generally in any case where a number is known to be within a certain limit on each side of the stated value, the limit of error is expressed by the sign ±. Thus the former of the above two statements would give 17 = ·14286 ± ·000005. It should be observed that the numerical value of the error is to be subtracted from or added to the stated value according as the error is positive or negative.
(iii) The limit of error can be expressed as a fraction of the number as stated. Thus 17 = ·143 ± ·0005 can be written 17 = 143(1 ± 1286).
83. Accuracy after Arithmetical Operations.—If the numbers which are the subject of operations are not all exact, the accuracy of the result requires special investigation in each case.
Additions and subtractions are simple. If, for instance, the values of a and b, correct to two places of decimals, are 3·58 and 1·34, then 2·24, as the value of a − b, is not necessarily correct to two places. The limit of error of each being ±·005, the limit of error of their sum or difference is ±·01.
For multiplication we make use of the formula (§ 60 (i)) (a′ ± α)(b′ ± αβ) = a′b′ + aαβ ± (a′αβ + b′α). If a′ and b′ are the stated values, and ± α and ± αβ the respective limits of error, we ought strictly to take a′b′ + αβ as the product, with a limit of error ± (a′αβ + b′α). In practice, however, both αβ and a certain portion of a′b′ are small in comparison with a′αβ and b′α, and we therefore replace a′b′ + αβ by an approximate value, and increase the limit of error so as to cover the further error thus introduced. In the case of the two numbers given in the last paragraph, the product lies between 3·575 × 1·335 = 4·772625 and 3·585 × 1·345 = 4·821825. We might take the product as (3·58 × 1·34) + (·005)2 = 4·797225, the limits of error being ± ·005 (3·58 + 1·34) = ± ·0246; but it is more convenient to write it in such a form as 4·797 ± ·025 or 4·80 ± ·03.
If the number of decimal places to which a result is to be accurate is determined beforehand, it is usually not necessary in the actual working to go to more than two or three places beyond this. At the close of the work the extra figures are dropped, the last figure which remains being corrected (§ 82 (i)) if necessary.
VIII. Surds and Logarithms
84. Roots and Surds.—The pth root of a number (§ 43) may, if the number is an integer, be found by expressing it in terms of its prime factors; or, if it is not an integer, by expressing it as a fraction in its lowest terms, and finding the pth roots of the numerator and of the denominator separately. Thus to find the cube root of 1728, we write it in the form 26.33, and find that its cube root is 22.3 = 12; or, to find the cube root of 1·728, we write it as 17281000 = 216125 = 23.3353, and find that the cube root is 2.35 = 1·2. Similarly the cube root of 2197 is 13. But we cannot find any number whose cube is 2000.
It is, however, possible to find a number whose cube shall approximate as closely as we please to 2000. Thus the cubes of 12·5 and of 12·6 are respectively 1953·125 and 2000·376, so that the number whose cube differs as little as possible from 2000 is somewhere between 12·5 and 12·6. Again the cube of 12·59 is 1995·616979, so that the number lies between 12·59 and 12·60. We may therefore consider that there is some number x whose cube is 2000, and we can find this number to any degree of accuracy that we please.
A number of this kind is called a surd; the surd which is the pth root of N is written p√N, but if the index is 2 it is usually omitted, so that the square root of N is written √N.
85. Surd as a Power.—We have seen (§§ 43, 44) that, if we take the successive powers of a number N, commencing with 1, they may be written N0, N1, N2, N3, . . ., the series of indices being the standard series; and we have also seen (§ 44) that multiplication of any two of these numbers corresponds to addition of their indices. Hence we may insert in the power-series numbers with fractional indices, provided that the multiplication of these numbers follows the same law. The number denoted by N13 will therefore be such that N13 × N13 × N13 = N13 + 13 + 13 = N; i.e. it will be the cube root of N. By analogy with the notation of fractional numbers, N23 will be N13 + 13 = N13 × N13; and, generally, Npq will mean the product of p numbers, the product of q of which is equal to N. Thus N26 will not mean the same as N13, but will mean the square of N16; but this will be equal to N13, i.e. (6√N)2 = 3√N.
86. Multiplication and Division of Surds.—To add or subtract fractional numbers, we must reduce them to a common denominator; and similarly, to multiply or divide surds, we must express them as power-numbers with the same index. Thus 3√2 × √5 = 213 × 512 = 226 × 536 = 416 × 12516 = 50016 = 6√500.
87. Antilogarithms.—If we take a fixed number, e.g. 2, as base, and take as indices the successive decimal numbers to any particular number of places of decimals, we get a series of antilogarithms of the indices to this base. Thus, if we go to two places of decimals, we have as the integral series the numbers 1, 2, 4, 8, . . . which are the values of 20, 21, 22, . . . and we insert within this series the successive powers of x, where x is such that x100 = 2. We thus get the numbers 2·01, 2·02, 2·03, . . ., which are the antilogarithms of ·01, ·02, ·03, . . . to base 2; the first antilogarithm being 2·00 = 1, which is thus the antilogarithm of 0 to this (or any other) base. The series is formed by successive multiplication, and any antilogarithm to a larger number of decimal places is formed from it in the same way by multiplication. If, for instance, we have found 2·31, then the value of 2·316 is found from it by multiplying by the 6th power of the 1000th root of 2.
For practical purposes the number taken as base is 10; the convenience of this being that the increase of the index by an integer means multiplication by the corresponding power of 10, i.e. it means a shifting of the decimal point. In the same way, by dividing by powers of 10 we may get negative indices.
88. Logarithms.—If N is the antilogarithm of p to the base a, i.e. if N = ap, then p is called the logarithm of N to the base a, and is written loga N. As the table of antilogarithms is formed by successive multiplications, so the logarithm of any given number is in theory found by successive divisions. Thus, to find the logarithm of a number to base 2, the number being greater than 1, we first divide repeatedly by 2 until we get a number between 1 and 2; then divide repeatedly by 10√2 until we get a number between 1 and 10√2; then divide repeatedly by 100√2; and so on. If, for instance, we find that the number is approximately equal to 23 × (10√2)5 × (100√2)7 × (1000√2)4, it may be written 23.574, and its logarithm to base 2 is 3.574.
For a further explanation of logarithms, and for an explanation of the treatment of cases in which an antilogarithm is less than 1, see Logarithm.
For practical purposes logarithms are usually calculated to base 10, so that log10 10 = 1, log10 100 = 2, &c.
IX. Units
89. Change of Denomination of a numerical quantity is usually called reduction, so that this term covers, e.g., the expression of £153, 7s. 4d. as shillings and pence and also the expression of 3067s. 4d. as £, s. and d.
The usual statement is that to express £153, 7s. as shillings we multiply 153 by 20 and add 7. This, as already explained (§ 37), is incorrect. £153 denotes 153 units, each of which is £1 or 20s.; and therefore we must multiply 20s. by 153 and add 7s., i.e. multiply 20 by 153 (the unit being now 1s.) and add 7. This is the expression of the process on the grouping method. On the counting method we have a scale with every 20th shilling marked as a £; there are 153 of these 20’s, and 7 over.
The simplest case, in which the quantity can be expressed as an integral number of the largest units involved, has already been considered (§§ 37, 42). The same method can be applied in other cases by regarding a quantity expressed in several denominations as a fractional number of units of the largest denomination mentioned; thus 7s. 4d. is to be taken as meaning 7412s., but £0, 7s. 4d. as £0741220 (§17). The reduction of £153, 7s. 4d. to pence, and of 36808d. to £, s. d., on this principle, is shown in diagrams A and B above.
For reduction of pounds to shillings, or shillings to pounds, we must consider that we have a multiple-table (§ 36) in which the multiples of £1 and of 20s. are arranged in parallel columns; and similarly for shillings and pence.
90. Change of Unit.—The statement “£153 = 3060s.” is not a statement of equality of the same kind as the statement “153 × 20 = 3060,” but only a statement of equivalence for certain purposes; in other words, it does not convey an absolute truth. It is therefore of interest to see whether we cannot replace it by an absolute truth.
To do this, consider what the ordinary processes of multiplication and division mean in reference to concrete objects. If we want to give, to 5 boys, 4 apples each, we are said to multiply 4 apples by 5. We cannot multiply 4 apples by 5 boys, for then we should get 20 “boy-apples,” an expression which has no meaning. Or, again, to distribute 20 apples amongst 5 boys, we are not regarded as dividing 20 apples by 5 boys, but as dividing 20 apples by the number 5. The multiplication or division here involves the omission of the unit “boy,” and the operation is incomplete. The complete operation, in each case, is as follows.
(i) In the case of multiplication we commence with the conception of the number “5” and the unit “boy”; and we then convert this unit into 4 apples, and thus obtain the result, 20 apples. The conversion of the unit may be represented as multiplication by a factor 4 apples1 boy, so that the operation is 4 apples1 boy × 5 boys = 5 × 4 apples1 boy × 1 boy = 5 × 4 apples = 20 apples. Similarly, to convert £153 into shillings we must multiply it by a factor 20£1, so that we get
20£1 × £153＝153 × 20£1 × £1＝153 × 20s.＝3060s.
Hence we can only regard £153 as being equal to 3060s. if we regard this converting factor as unity.
(ii) In the case of partition we can express the complete operation if we extend the meaning of division so as to enable us to divide 20 apples by 5 boys. We thus get 20 apples5 boys = 4 apples1 boy, which means that the distribution can be effected by distributing at the rate of 4 apples per boy. The converting factor mentioned under (i) therefore represents a rate; and partition, applied to concrete cases, leads to a rate.
In reference to the use of the sign × with the converting factor, it should be observed that “7 ℔4 ℔ ×” symbolizes the replacing of so many times 4 ℔ by the same number of times 7 ℔, while “74 ×” symbolizes the replacing of 4 times something by 7 times that something.
X. Arithmetical Reasoning
91. Correspondence of Series of Numbers.—In §§ 33-42 we have dealt with the parallelism of the original number-series with a series consisting of the corresponding multiples of some unit, whether a number or a numerical quantity; and the relations arising out of multiplication, division, &c., have been exhibited by diagrams comprising pairs of corresponding terms of the two series. This, however, is only a particular case of the correspondence of two series. In considering addition, for instance, we have introduced two parallel series, each being the original number-series, but the two being placed in different positions. If we add 1, 2, 3, . . . to 6, we obtain a series 7, 8, 9, . . . , the terms of which correspond with those of the original series 1, 2, 3, . . .
Again, in §§ 61-75 and 84-88 we have considered various kinds of numbers other than those in the original number-series. In general, these have involved two of the original numbers, e.g. 53 involves 5 and 3, and log2 8 involves 2 and 8. In some cases, however, e.g. in the case of negative numbers and reciprocals, only one is involved; and there might be three or more, as in the case of a number expressed by (a + b)n. If all but one of these constituent elements are settled beforehand, e.g. if we take the numbers 5, 52, 53, . . ., or the numbers 3√1, 3√2, 3√3, . . . or log10 1.001, log10 1.002, log10 1.003 . . . we obtain a series in which each term corresponds with a term of the original number-series.
This correspondence is usually shown by tabulation, i.e. by the formation of a table in which the original series is shown in one column, and each term of the second series is placed in a second column opposite the corresponding term of the first series, each column being headed by a description of its contents. It is sometimes convenient to begin the first series with 0, and even to give the series of negative numbers; in most cases, however, these latter are regarded as belonging to a different series, and they need not be considered here. The diagrams, A, B, C are simple forms of tables; A giving a sum-series, B a multiple-series, and C a series of square roots, calculated approximately.
92. Correspondence of Numerical Quantities.—Again, in § 89, we have considered cases of multiple-tables of numerical quantities, where each quantity in one series is equivalent to the corresponding quantity in the other series. We might extend this principle to cases in which the terms of two series, whether of numbers or of numerical quantities, merely correspond with each other, the correspondence being the result of some relation. The volume of a cube, for instance, bears a certain relation to the length of an edge of the cube. This relation is not one of proportion; but it may nevertheless be expressed by tabulation, as shown at D.
93. Interpolation.—In most cases the quantity in the second column may be regarded as increasing or decreasing continuously as the number in the first column increases, and it has intermediate values corresponding to intermediate (i.e. fractional or decimal) numbers not shown in the table. The table in such cases is not, and cannot be, complete, even up to the number to which it goes. For instance, a cube whose edge is 112 in. has a definite volume, viz. 338 cub. in. The determination of any such intermediate value is performed by Interpolation (q.v.).
In treating a fractional number, or the corresponding value of the quantity in the second column, as intermediate, we are in effect regarding the numbers 1, 2, 3, . . ., and the corresponding numbers in the second column, as denoting points between which other numbers lie, i.e. we are regarding the numbers as ordinal, not cardinal. The transition is similar to that which arises in the case of geometrical measurement (§ 26), and it is an essential feature of all reasoning with regard to continuous quantity, such as we have to deal with in real life.
94. Nature of Arithmetical Reasoning.—The simplest form of arithmetical reasoning consists in the determination of the term in one series corresponding to a given term in another series, when the relation between the two series is given; and it implies, though it does not necessarily involve, the establishment of each series as a whole by determination of its unit. A method involving the determination of the unit is called a unitary method. When the unit is not determined, the reasoning is algebraical rather than arithmetical. If, for instance, three terms of a proportion are given, the fourth can be obtained by the relation given at the end of § 57, this relation being then called the Rule of Three; but this is equivalent to the use of an algebraical formula.
More complicated forms of arithmetical reasoning involve the use of series, each term in which corresponds to particular terms in two or more series jointly; and cases of this kind are usually dealt with by special methods, or by means of algebraical formulae. The old-fashioned problems about the amount of work done by particular numbers of men, women and boys, are of this kind, and really involve the solution of simultaneous equations. They are not suitable for elementary purposes, as the arithmetical relations involved are complicated and difficult to grasp.
XI. Methods of Calculation
(i.) Exact Calculation.
95. Working from Left.—It is desirable, wherever possible, to perform operations on numbers or numerical quantities from the left, rather than from the right. There are several reasons for this. In the first place, an operation then corresponds more closely, at an elementary stage, with the concrete process which it represents. If, for instance, we had one sum of £3, 15s. 9d. and another of £2, 6s. 5d., we should add them by putting the coins of each denomination together and commencing the addition with the £. In the second place, this method fixes the attention at once on the larger, and therefore more important, parts of the quantities concerned, and thus prevents arithmetical processes from becoming too abstract in character. In the third place, it is a better preparation for dealing with approximate calculations. Finally, experience shows that certain operations in which the result is written down at once—e.g. addition or subtraction of two numbers or quantities, and multiplication by some small numbers—are with a little practice performed more quickly and more accurately from left to right.
96. Addition.—There is no difference in principle between addition (or subtraction) of numbers and addition (or subtraction) of numerical quantities. In each case the grouping system involves rearrangement, which implies the commutative law, while the counting system requires the expression of a quantity in different denominations to be regarded as a notation in a varying scale (§§ 17, 32). We need therefore consider numerical quantities only, our results being applicable to numbers by regarding the digits as representing multiples of units in different denominations.
When the result of addition in one denomination can be partly expressed in another denomination, the process is technically called carrying. The name is a bad one, since it does not correspond with any ordinary meaning of the verb. It would be better described as exchanging, by analogy with the “changing” of subtraction. When, e.g., we find that the sum of 17s. and 18s. is 35s., we take out 20 of the 35 shillings, and exchange them for £1.
To add from the left, we have to look ahead to see whether the next addition will require an exchange. Thus, in adding £3, 17s. 0d. to £2, 18s. 0d., we write down the sum of £3 and £2 as £6, not as £5, and the sum of 17s. and 18s. as 15s., not as 35s.
When three or more numbers or quantities are added together, the result should always be checked by adding both upwards and downwards. It is also useful to look out for pairs of numbers or quantities which make 1 of the next denomination, e.g. 7 and 3, or 8d. and 4d.
97. Subtraction.—To subtract £3, 5s. 4d. from £9, 7s. 8d., on the grouping system, we split up each quantity into its denominations, perform the subtractions independently, and then regroup the results as the “remainder” £6, 2s. 4d. On the counting system we can count either forwards or backwards, and we can work either from the left or from the right. If we count forwards we find that to convert £3, 5s. 4d. into £9, 7s. 8d. we must successively add £6, 2s. and 4d. if we work from the left, or 4d., 2s. and £6 if we work from the right. The intermediate values obtained by the successive additions are different according as we work from the left or from the right, being £9, 5s. 4d. and £9, 7s. 4d. in the one case, and £3, 5s. 8d. and £3, 7s. 8d. in the other. If we count backwards, the intermediate values are £3, 7s. 8d. and £3, 5s. 8d. in the one case, and £9, 7s. 4d. and £9, 5s. 4d. in the other.
The determination of each element in the remainder involves reference to an addition-table. Thus to subtract 5s. from 7s. we refer to an addition-table giving the sum of any two quantities, each of which is one of the series 0s., 1s., . . . 19s.
Subtraction by counting forward is called complementary addition.
To subtract £3, 5s. 8d. from £9, 10s. 4d., on the grouping system, we must change 1s. out of the 10s. into 12d., so that we subtract £3, 5s. 8d. from £9, 9s. 16d. On the counting system it will be found that, in determining the number of shillings in the remainder, we subtract 5s. from 9s. if we count forwards, working from the left, or backwards, working from the right; while, if we count backwards, working from the left, or forwards, working from the right, the subtraction is of 6s. from 10s. In the first two cases the successive values (in direct or reverse order) are £3, 5s. 8d., £9, 5s. 8d., £9, 9s. 8d. and £9, 10s. 4d.; while in the last two cases they are £9, 10s. 4d., £3, 10s. 4d., £3, 6s. 4d. and £3, 5s. 8d.
In subtracting from the left, we look ahead to see whether a 1 in any denomination must be reserved for changing; thus in subtracting 274 from 637 we should put down 2 from 6 as 3, not as 4, and 7 from 3 as 6.
98. Multiplication-Table.—For multiplication and division we use a multiplication-table, which is a multiple-table, arranged as explained in § 36, and giving the successive multiples, up to 9 times or further, of the numbers from 1 (or better, from 0) to 10, 12 or 20. The column (vertical) headed 3 will give the multiples of 3, while the row (horizontal) commencing with 3 will give the values of 3 × 1, 3 × 2, . . . To multiply by 3 we use the row. To divide by 3, in the sense of partition, we also use the row; but to divide by 3 as a unit we use the column.
99. Multiplication by a Small Number.—The idea of a large multiple of a small number is simpler than that of a small multiple of a large number, but the calculation of the latter is easier. It is therefore convenient, in finding the product of two numbers, to take the smaller as the multiplier.
To find 3 times 427, we apply the distributive law (§ 58 (vi)) that 3.427 = 3(400 + 20 + 7) = 3.400 + 3.20 + 3.7. This, if we regard 3.427 as 427 + 427 + 427, is a direct consequence of the commutative law for addition (§ 58 (iii)), which enables us to add separately the hundreds, the tens and the ones. To find 3.400, we treat 100 as the unit (as in addition), so that 3.400 = 3.4.100 = 12.100 = 1200; and similarly for 3.20. These are examples of the associative law for multiplication (§ 58 (iv)).
100. Special Cases.—The following are some special rules:—
(i) To multiply by 5, multiply by 10 and divide by 2. (And conversely, to divide by 5, we multiply by 2 and divide by 10.)
(ii) In multiplying by 2, from the left, add 1 if the next figure of the multiplicand is 5, 6, 7, 8 or 9.
(iii) In multiplying by 3, from the left, add 1 when the next figures are not less than 33 . . . 334 and not greater than 66 . . . 666, and 2 when they are 66 . . . 667 and upwards.
(iv) To multiply by 7, 8, 9, 11 or 12, treat the multiplier as 10 − 3, 10 − 2, 10 − 1, 10 + 1 or 10 + 2; and similarly for 13, 17, 18, 19, &c.
(v) To multiply by 4 or 6, we can either multiply from the left by 2 and then by 2 or 3, or multiply from the right by 4 or 6; or we can treat the multiplier as 5 − 1 or 5 + 1.
101. Multiplication by a Large Number.—When both the numbers are large, we split up one of them, preferably the multiplier, into separate portions. Thus 231.4273 = (200 + 30 + 1).4273 = 200.4273 + 30.4273 + 1.4273. This gives the partial products, the sum of which is the complete products. The process is shown fully in A below,—
and more concisely in B. To multiply 4273 by 200, we use the commutative law, which gives 200.4273 = 2 × 100 × 4273 = 2 × 4273 × 100 = 8546 × 100 = 854600; and similarly for 30.4273. In B the terminal 0’s of the partial products are omitted. It is usually convenient to make out a preliminary table of multiples up to 10 times; the table being checked at 5 times (§ 100) and at 10 times.
The main difficulty is in the correct placing of the curtailed partial products. The first step is to regard the product of two numbers as containing as many digits as the two numbers put together. The table of multiples will them be as in C. The next step is to arrange the multiplier and the multiplicand above the partial products. For elementary work the multiplicand may come immediately after the multiplier, as in D; the last figure of each partial product then comes immediately under the corresponding figure of the multiplier. A better method, which leads up to the multiplication of decimals and of approximate values of numbers, is to place the first figure of the multiplier under the first figure of the multiplicand, as in E; the first figure of each partial product will then come under the corresponding figure of the multiplier.
102. Contracted Multiplication.—The partial products are sometimes omitted; the process saves time in writing, but is not easy. The principle is that, e.g. (a.102 + b.10 + c)(p.102 + q.10 + r ) = ap.104 + (aq + bp) 103 + (ar + bq + cp) 102 + (br + cq) 10 + cr. Hence the digits are multiplied in pairs, and grouped according to the power of 10 which each product contains. A method of performing the process is shown here for the case of 162.427. The principle is that 162.427 = 100.427 + 60.427 + 2.427 = 1.42700 + 6.4270 + 2.427; but, instead of writing down the separate products, we (in effect) write 42700, 4270, and 427 in separate rows, with the multipliers 1, 6, 2 in the margin, and then multiply each number in each column by the corresponding multiplier in the margin, making allowance for any figures to be “carried.” Thus the second figure (from the right) is given by 1 + 2.2 + 6.7 = 47, the 1 being carried.
103. Aliquot Parts.—For multiplication by a proper fraction or a decimal, it is sometimes convenient, especially when we are dealing with mixed quantities, to convert the multiplier into the sum or difference of a number of fractions, each of which has 1 as its numerator. Such fractions are called aliquot parts (from Lat. aliquot, some, several). This can usually be done in a good many ways. Thus 56 = 1 − 16, and also = 12 + 13; and 15% = ·15 = 110 + 120 = 16 − 160 = 18 + 140. The fractions should generally be chosen so that each part of the product may be obtained from an earlier part by a comparatively simple division. Thus 12 + 120 − 160 is a simpler expression for 815 than 12 + 130.
The process may sometimes by applied two or three times in succession; thus 815 = 45·23 = (1 − 15)(1 − 13), and 3340 = 34·1110 = (1 − 14)(1 + 110).
104. Practice.—The above is a particular case of the method called practice, but the nomenclature of the method is confusing. There are two kinds of practice, simple practice and compound practice, but the latter is the simpler of the two. To find the cost of 2 ℔ 8 oz. of butter at 1s. 2d. a ℔, we multiply 1s. 2d. by 2816 = 212. This straightforward process is called “compound” practice. “Simple” practice involves an application of the commutative law. To find the cost of n articles at £a, bs, cd. each, we express £a, bs, cd. in the form £(a + f ), where f is a fraction (or the sum of several fractions); we then say that the cost, being n × £(a + f ), is equal to (a + f ) × £n, and apply the method of compound practice, i.e. the method of aliquot parts.
105. Multiplication of a Mixed Number.—When a mixed quantity or a mixed number has to be multiplied by a large number, it is sometimes convenient to express the former in terms of one only of its denominations. Thus, to multiply £7, 13s. 6d. by 469, we may express the former in any of the ways £7·675, 30740 of £1, 15312s., 153·5s., 307 sixpences, or 1842 pence. Expression in £ and decimals of £1 is usually recommended, but it depends on circumstances whether some other method may not be simpler.
A sum of money cannot be expressed exactly as a decimal of £1 unless it is a multiple of 34d. A rule for approximate conversion is that 1s. = ·05 of £1, and that 212d.= ·01 of £1. For accurate conversion we write ·1£ for each 2s., and ·001£ for each farthing beyond 2s., their number being first increased by one twenty-fourth.
106. Division.—Of the two kinds of division, although the idea of partition is perhaps the more elementary, the process of measuring is the easier to perform, since it is equivalent to a series of subtractions. Starting from the dividend, we in theory keep on subtracting the unit, and count the number of subtractions that have to be performed until nothing is left. In actual practice, of course, we subtract large multiples at a time. Thus, to divide 987063 by 427, we reverse the procedure of § 101, but with intermediate stages. We first construct the multiple-table C, and then subtract successively 200 times, 30 times and 1 times; these numbers being the partial quotients. The theory of the process is shown fully in F. Treating x as the unknown quotient corresponding to the original dividend, we obtain successive dividends corresponding to quotients x − 200, x − 230 and x − 231. The original dividend is written as 0987063, since its initial figures are greater than those of the divisor; if the dividend had commenced with (e.g.) 3 ... it would not have been necessary to insert the initial 0. At each stage of the division the number of digits in the reduced dividend is decreased by one. The final dividend being 0000, we have x − 231 = 0, and therefore x = 231.
107. Methods of Division.—What are described as different methods of division (by a single divisor) are mainly different methods of writing the successive figures occurring in the process. In long division the divisor is put on the left of the dividend, and the quotient on the right; and each partial product, with the remainder after its subtraction, is shown in full. In short division the divisor and the quotient are placed respectively on the left of and below the dividend, and the partial products and remainders are not shown at all. The Austrian method (sometimes called in Great Britain the Italian method) differs from these in two respects. The first, and most important, is that the quotient is placed above the dividend. The second, which is not essential to the method, is that the remainders are shown, but not the partial products; the remainders being obtained by working from the right, and using complementary addition. It is doubtful whether the brevity of this latter process really compensates for its greater difficulty.
The advantage of the Austrian arrangement of the quotient lies in the indication it gives of the true value of each partial quotient. A modification of the method, corresponding with D of § 101, is shown in G; the fact that the partial product 08546 is followed by two blank spaces shows that the figure 2 represents a partial quotient 200. An alternative arrangement, corresponding to E of § 101, and suited for more advanced work, is shown in H.
108. Division with Remainder.—It has so far been assumed that the division can be performed exactly, i.e. without leaving an ultimate remainder. Where this is not the case, difficulties are apt to arise, which are mainly due to failure to distinguish between the two kinds of division. If we say that the division of 41d. by 12 gives quotient 3d. with remainder 5d., we are speaking loosely; for in fact we only distribute 36d. out of the 41d., the other 5d. remaining undistributed. It can only be distributed by a subdivision of the unit; i.e. the true result of the division is 3512d. On the other hand, we can quite well express the result of dividing 41d. by 1s (= 12d.) as 3 with 5d. (not “5”) over, for this is only stating that 41d. = 3s. 5d.; though the result might be more exactly expressed as 3512s.
Division with a remainder has thus a certain air of unreality, which is accentuated when the division is performed by means of factors (§ 42). If we have to divide 935 by 240, taking 12 and 20 as factors, the result will depend on the fact that, in the notation of § 17, 
In incomplete partition the quotient is 3, and the remainders 11 and 17 are in effect disregarded; if, after finding the quotient 3, we want to know what remainder would be produced by a direct division, the simplest method is to multiply 3 by 240 and subtract the result from 935. In complete partition the successive quotients are 771112 and 317111220 = 3215240. Division in the sense of measuring leads to such a result as 935d. = £3, 17s. 11d.; we may, if we please, express the 17s. 11d. as 215d., but there is no particular reason why we should do so.
109. Division by a Mixed Number.—To divide by a mixed number, when the quotient is seen to be large, it usually saves time to express the divisor as either a simple fraction or a decimal of a unit of one of the denominations. Exact division by a mixed number is not often required in real life; where approximate division is required (e.g. in determining the rate of a “dividend”), approximate expression of the divisor in terms of the largest unit is sufficient.
110. Calculation of Square Root.—The calculation of the square root of a number depends on the formula (iii) of § 60. To find the square root of N, we first find some number a whose square is less than N, and subtract a2 from N. If the complete square root is a + b, the remainder after subtracting a2 is (2a + b)b. We therefore guess b by dividing the remainder by 2a, and form the product (2a + b)b. If this is equal to the remainder, we have found the square root. If it exceeds the square root, we must alter the value of b, so as to get a product which does not exceed the remainder. If the product is less than the remainder, we get a new remainder, which is N − (a + b)2; we then assume the full square root to be c, so that the new remainder is equal to (2a + 2b + c)c, and try to find c in the same way as we tried to find b.
An analogous method of finding cube root, based on the formula for (a + b)3, used to be given in text-books, but it is of no practical use. To find a root other than a square root we can use logarithms, as explained in § 113.
(ii.) Approximate Calculation.
111. Multiplication.—When we have to multiply two numbers, and the product is only required, or can only be approximately correct, to a certain number of significant figures, we need only work to two or three more figures (§ 83), and then correct the final figure in the result by means of the superfluous figures.
A common method is to reverse the digits in one of the numbers; but this is only appropriate to the old-fashioned method of writing down products from the right. A better method is to ignore the positions of the decimal points, and multiply the numbers as if they were decimals between ·1 and 1·0. The method E of § 101 being adopted, the multiplicand and the multiplier are written with a space after as many digits (of each) as will be required in the product (on the principle explained in § 101); and the multiplication is performed from the left, two extra figures being kept in. Thus, to multiply 27·343 by 3·1415927 to one decimal place, we require 2 + 1 + 1 = 4 figures in the product. The result is 085·9 = 85·9, the position of the decimal point being determined by counting the figures before the decimal points in the original numbers.
112. Division.—In the same way, in performing approximate division, we can at a certain stage begin to abbreviate the divisor, taking off one figure (but with correction of the final figure of the partial product) at each stage. Thus, to divide 85·9 by 3·1415927 to two places of decimals, we in effect divide ·0859 by ·31415927 to four places of decimals. In the work, as here shown, a 0 is inserted in front of the 859, on the principle explained in § 106. The result of the division is 27·34.
113. Logarithms.—Multiplication, division, involution and evolution, when the results cannot be exact, are usually most simply performed, at any rate to a first approximation, by means of a table of logarithms. Thus, to find the square root of 2, we have log √2 = log (212) = 12 log 2. We take out log 2 from the table, halve it, and then find from the table the number of which this is the logarithm. (See Logarithm.) The slide-rule (see Calculating Machines) is a simple apparatus for the mechanical application of the methods of logarithms.
When a first approximation has been obtained in this way, further approximations can be obtained in various ways. Thus, having found √2 = 1·414 approximately, we write √2 = 1·414 + θ, whence 2 = (1·414)2 + (2·818)θ + θ2. Since θ2 is less than 14 of (·001)2, we can obtain three more figures approximately by dividing 2−(1·414)2 by 2·818.
114. Binomial Theorem.—More generally, if we have obtained a as an approximate value for the pth root of N, the binomial theorem gives as an approximate formula p√N = a + θ, where N = ap + pap−1θ.
115. Series.—A number can often be expressed by a series of terms, such that by taking successive terms we obtain successively closer approximations. A decimal is of course a series of this kind, e.g. 3·14159 . . . means 3 + 1/10 + 4/102 + 1/103 + 5/104 + 9/105 + . . . A series of aliquot parts is another kind, e.g. 3·1416 is a little less than 3+17−1800.
Recurring Decimals are a particular kind of series, which arise from the expression of a fraction as a decimal. If the denominator of the fraction, when it is in its lowest terms, contains any other prime factors than 2 and 5, it cannot be expressed exactly as a decimal; but after a certain point a definite series of figures will constantly recur. The interest of these series is, however, mainly theoretical.
116. Continued Products.—Instead of being expressed as the sum of a series of terms, a number may be expressed as the product of a series of factors, which become successively more and more nearly equal to 1. For example,
3·1416＝3×1047210000＝3 × 13091250＝3 × 2221 × 24992500＝3(1 + 121)(1−12500).
Hence, to multiply by 3·1416, we can multiply by 317, and subtract 12500 (= ·0004) of the result; or, to divide by 3·1416, we can divide by 3, then subtract 122 of the result, and then add 12499 of the new result.
117. Continued Fractions.—The theory of continued fractions (q.v.) gives a method of expressing a number, in certain cases, as a continued product. A continued fraction, of the kind we are considering, is an expression of the form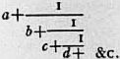 
where b, c, d, . . . are integers, and a is an integer or zero. The expression is usually written, for compactness, a + 1b+ 1c+ 1d+ &c. The numbers a, b, c, d, . . . are called the quotients.
Any exact fraction can be expressed as a continued fraction, and there are methods for expressing as continued fractions certain other numbers, e.g. square roots, whose values cannot be expressed exactly as fractions.
The successive values, a1, ab + 1b, . . ., obtained by taking account of the successive quotients, are called convergents, i.e. convergents to the true value. The following are the main properties of the convergents.
(i) If we precede the series of convergents by 01 and , then the numerator (or denominator) of each term of the series 01, 10, a1, ab+1b . . ., after the first two, is found by multiplying the numerator (or denominator) of the last preceding term by the corresponding quotient and adding the numerator (or denominator) of the term before that. If a is zero, we may regard 1b as the first convergent, and precede the series by 10 and 11.
(ii) Each convergent is a fraction in its lowest terms.
(iii) The convergents are alternately less and greater than the true value.
(iv) Each convergent is nearer to the true value than any other fraction whose denominator is less than that of the convergent.
(v) The difference of two successive convergents is the reciprocal of the product of their denominators; e.g. ab + 1b − a1 = 11·b, and abc + c + abc + 1−ab + 1b = −1b(bc + 1).
It follows from these last three properties that if the successive convergents are p11, p2q2, p3q3, . . . the number can be expressed in the form p1(1 + 1p1q2) (1 − 1p2q3 (1 + 1p3q4) . . . , and that if we go up to the factor 1 ± 1pnqn + 1 the product of these factors differs from the true value of the number by less than ±1qnqn + 1.
In certain cases two or more factors can be combined so as to produce an expression of the form 1 ± 1k, where k is an integer. For instance, 3·1415927 = 3(1 + 13·7) (1 − 122·106) (1 + 1333·113) ...; but the last two of these factors may be combined as (1 − 122·113). Hence 3·1415927 = 31·2221·24852486 . . .
XII. Applications
(i.) Systems of Measures.[1]
118. Metric System.—The metric system was adopted in France at the end of the 18th century. The system is decimal throughout. The principal units of length, weight and volume are the metre, gramme (or gram) and litre. Other units are derived from these by multiplication or division by powers of 10, the names being denoted by prefixes. The prefixes for multiplication by 10, 102, 103 and 104 are deca-, hecto-, kilo- and myria-, and those for division by 10, 102 and 103 are deci-, centi- and milli-; the former being derived from Greek, and the latter from Latin. Thus kilogramme means 1000 grammes, and centimetre means 1100 of a metre. There are also certain special units, such as the hectare, which is equal to a square hectometre, and the micron, which is 11000 of a millimetre.
The metre and the gramme are defined by standard measures preserved at Paris. The litre is equal to a cubic decimetre. The gramme was intended to be equal to the weight of a cubic centimetre of pure water at a certain temperature, but the equality is only approximate.
The metric system is now in use in the greater part of the civilized world, but some of the measures retain the names of old disused measures. In Germany, for instance, the Pfund is 12 kilogramme, and is approximately equal to 1110 ℔ English.
119. British Systems.—The British systems have various origins, and are still subject to variations caused by local usage or by the usage of particular businesses. The following tables are given as illustrations of the arrangement adopted elsewhere in this article; the entries in any column denote multiples or submultiples of the unit stated at the head of the column, and the entries in any row give the expression of one unit in term of the other units.
| Inch. | Foot. | Yard. | Chain. | Furlong. | Mile. |
| 1 | 112 | 136 | 1792 | 17920 | 163360 |
| 12 | 1 | 13 | 166 | 1660 | 15280 |
| 36 | 3 | 1 | 122 | 1220 | 11760 |
| 792 | 66 | 22 | 1 | 10 | 180 |
| 7920 | 660 | 220 | 10 | 1 | 18 |
| 63360 | 5280 | 1760 | 80 | 8 | 1 |
| Ounce. | Pound. | Stone. | Quarter. | Hundred- weight. |
Ton. |
| 1 | 116 | 1224 | 1448 | 11792 | 133840 |
| 16 | 1 | 114 | 128 | 1112 | 12240 |
| 224 | 14 | 1 | 12 | 18 | 1160 |
| 448 | 28 | 2 | 1 | 14 | 180 |
| 1792 | 112 | 8 | 4 | 1 | 120 |
| 33840 | 2240 | 160 | 80 | 20 | 1 |
(Also 7000 grains＝1 ℔ avoirdupois.)
120. Change of System.—It is sometimes necessary, when a quantity is expressed in one system, to express it in another, The following are the ratios of some of the units; each unit is expressed approximately as a decimal of the other, and their ratio is shown as a continued product (§ 116), a few of the corresponding convergents to the continued fraction (§ 117) being added in brackets. It must be remembered that the number expressing any quantity in terms of a unit is inversely proportional to the magnitude of the unit, i.e. the number of new units is to be found by multiplying the number of old units by the ratio of the old unit to the new unit.
| YardMetre | =914410000 | =1000010936 | =1112·384385·82258224 . . . | (1112,3235=87·45,235257). |
| InchCentimetre | =2540010000 | =100003937 | =52·6665·16511650 . . . | (52,3313,12750). |
| MileKilometre | =1609310000 | =100006214 | =85·185184·23692368 . . . | (85,3723,10364). |
| Square YardSquare Metre | =836110000 | =1000011960 | =56·306305·1525015249 . . . | (56,5161,250299). |
| AcreHectare | =404710000 | =1000024711 | =25·8584·53205321 . . . | (25,1742,380939). |
| QuartLitre | =1136510000 | =100008799 | =87·175176·89768975 . . . | (87,2522,408359). |
| PoundKilogramme | =453610000 | =1000022046 | =12·1011·484485·2939129392 . . . | (12,511,4497,303668). |
(ii.) Special Applications.
121. Commercial Arithmetic.—This term covers practically all dealings with money which involve the application of the principle of proportion. A simple class of cases is that which deals with equivalence of sums of money in different currencies; these cases really come under § 120. In other cases we are concerned with a proportion stated as a numerical percentage, or as a money percentage (i.e. a sum of money per £100), or as a rate in the £ or the shilling. The following are some examples. Percentage: Brokerage, commission, discount, dividend, interest, investment, profit and loss. Rate in the £: Discount, dividend, rates, taxes. Rate in the shilling: Discount.
Text-books on arithmetic usually contain explanations of the chief commercial transactions in which arithmetical calculations arise; it will be sufficient in the present article to deal with interest and discount, and to give some notes on percentages and rates in the £. Insurance and Annuities are matters of general importance, which are dealt with elsewhere under their own headings.
122. Percentages and Rates in the £.—In dealing with percentages and rates it is important to notice whether the sum which is expressed as a percentage of a rate on another sum is a part of or an addition to that sum, or whether they are independent of one another. Income tax, for instance, is calculated on income, and is in the nature of a deduction from the income; but local rates are calculated in proportion to certain other payments, actual or potential, and could without absurdity exceed 20s. in the £.
It is also important to note that if the increase or decrease of an amount A by a certain percentage produces B, it will require a different percentage to decrease or increase B to A. Thus, if B is 20% less than A, A is 25% greater than B.
123. Interest is usually calculated yearly or half-yearly, at a certain rate per cent. on the principal. In legal documents the rate is sometimes expressed as a certain sum of money “per centum per annum”; here “centum” must be taken to mean “£100.”
Simple interest arises where unpaid interest accumulates as a debt not itself bearing interest; but, if this debt bears interest, the total, i.e. interest and interest on interest, is called compound interest. If 100r is the rate per cent. per annum, the simple interest on £A for n years is £nrA, and the compound interest (supposing interest payable yearly) is £[(1 + r)n − 1]A. If n is large, the compound interest is most easily calculated by means of logarithms.
124. Discount is of various kinds. Tradesmen allow discount for ready money, this being usually at so much in the shilling or £. Discount may be allowed twice in succession off quoted prices; in such cases the second discount is off the reduced price, and therefore it is not correct to add the two rates of discount together. Thus a discount of 20%, followed by a further discount of 25%, gives a total discount of 40%, not 45%, off the original amount. When an amount will fall due at some future date, the present value of the debt is found by deducting discount at some rate per cent. for the intervening period, in the same way as interest to be added is calculated. This discount, of course, is not equal to the interest which the present value would produce at that rate of interest, but is rather greater, so that the present value as calculated in this way is less than the theoretical present value.
125. Applications to Physics are numerous, but are usually only of special interest. A case of general interest is the measurement of temperature. The graduation of a thermometer is determined by the freezing-point and the boiling-point of water, the interval between these being divided into a certain number of degrees, representing equal increases of temperature. On the Fahrenheit scale the points are respectively 32° and 212°; on the Centigrade scale they are 0° and 100°; and on the Réaumur they are 0° and 80°. From these data a temperature as measured on one scale can be expressed on either of the other two scales.
126. Averages occur in statistics, economics, &c. An average is found by adding together several measurements of the same kind and dividing by the number of measurements. In calculating an average it should be observed that the addition of any numerical quantity (positive or negative) to each of the measurements produces the addition of the same quantity to the average, so that the calculation may often be simplified by taking some particular measurement as a new zero from which to measure.
Authorities.—For the history of the subject, see W. W. R. Ball, Short History of Mathematics (1901), and F. Cajori, History of Elementary Mathematics (1896); or more detailed information in M. Cantor, Vorlesungen über Geschichte der Mathematik (1894–1901). L. C. Conant, The Number-Concept (1896), gives a very full account of systems of numeration. For the latter, and for systems of notation, reference may also be made to Peacock’s article “Arithmetic” in the Encyclopaedia Metropolitana, which contains a detailed account of the Greek system. F. Galton, Inquiries into Human Faculty (1883), contains the first account of number-forms; for further examples and references see D. E. Phillips, “Genesis of Number-Forms,” American Journal of Psychology, vol. viii. (1897). There are very few works dealing adequately but simply with the principles of arithmetic. Homersham Cox, Principles of Arithmetic (1885), is brief and lucid, but is out of print. The Psychology of Number, by J. A. McLellan and J. Dewey (1895), contains valuable suggestions (some of which have been utilized in the present article), but it deals only with number as the measure of quantity, and requires to be read critically. This work contains references to Grube’s system, which has been much discussed in America: for a brief explanation, see L. Seeley, The Grube Method of Teaching Arithmetic (1890). On the teaching of arithmetic, and of elementary mathematics generally, see J. W. A. Young, The Teaching of Mathematics in the Elementary and the Secondary School (1907); D. E. Smith, The Teaching of Elementary Mathematics (1900), also contains an interesting general sketch; W. P. Turnbull, The Teaching of Arithmetic (1903), is more elaborate. E. M. Langley, A Treatise on Computation (1895), has notes on approximate and abbreviated calculation. Text-books on arithmetic in general and on particular applications are numerous, and any list would soon be out of date. Recent English works have been influenced by the brief Report on the Teaching of Elementary Mathematics, issued by the Mathematical Association (1905); but this is critical rather than constructive. The Association has also issued a Report on the Teaching of Mathematics in Preparatory Schools (1907). In the United States of America the Report of the Committee of Ten on secondary school studies (1893) and the Report of the Committee of Fifteen on elementary education (1893–1894), both issued by the United States Bureau of Education, have attracted a good deal of attention. Sir O. Lodge, Easy Mathematics, chiefly Arithmetic (1905), treats the subject broadly in its practical aspects. The student who is interested in elementary teaching should consult the annual bibliographies in the Pedagogical Seminary; an article by D. E. Phillips in vol. v. (October 1897) contains references to works dealing with the psychological aspect of number. For an account of German methods, see W. King, Report on Teaching of Arithmetic and Mathematics in the Higher Schools of Germany (1903). (W. F. Sh.)
- ↑ See also Weights and Measures.