1911 Encyclopædia Britannica/Potentiometer
POTENTIOMETER, an instrument for the measurement of electromotive force and also of difference of electric potential between two points. The term potentiometer is usually applied to an instrument for the measurement of steady or continuous potential difference between two points in terms of the potential difference of the terminals of a standard voltaic cell of some kind, such as a Clark or Weston cell. The modern potentiometer has been developed out of an arrangement due to J. C. Poggendorff, employed also by J. Latimer Clark. but converted into its modern direct reading form by J. A. Fleming in 1885 (see Industries, 1886, i. 152). In principle the modern potentiometer consists of an arrangement by means of which any potential difference not exceeding a certain assigned value can be compared with that of a standard cell having a known electromotive force. In simplest form it consists of a long, straight, fine, uniform wire stretched over a divided scale. The ends of this wire are connected to one or more secondary cells of constant electromotive force, a variable resistance being interposed so as to regulate the current flowing through the fine wire. To one end of this fine wire is attached one terminal of a sensitive galvanometer. Sliding contacts can be moved along the fine wire into any position. Supposing that the scale under this wire is divided into 2000 parts and that we are in possession of a standard Clark cell, the electromotive force being known at various temperatures, and equal, say, to 1·434 volts at 15° C. The first process is to set the potentiometer. The slider is placed so as to touch the fine wire at division No. 1434 on the fine wire, and the Clark cell is connected in between the sliding contact and one terminal of the galvanometer, so that its negative pole is connected through the galvanometer with that end of the fine wire to which the negative pole of the working battery is attached. The resistance in circuit with the fine wire is then altered until the galvanometer shows no reflexion. We then know that the fall of potential down the 2000 divisions of the line wire must be exactly 2 volts. If then we substitute for the standard cell any other source of electromotive force, we can move the slider into another position in which the galvanometer will show no deflection. The scale reading then indicates directly the electromotive force of this second source of potential. Thus, for instance, if an experiment were made with a Leclanché cell, and if the balancing-point were found to be at 1500 divisions on the scale, the electromotive force would be determined as 1·500 volts. Instead of adjusting in this manner the electromotive force of any form of cell, if we pass any constant current through a known resistance and bring wires from the extremities of that resistance into connexion with the slider and the galvanometer terminal, we can in the same way determine the fall of potential down the above resistance in terms of the electromotive force of the standard cell and thus measure the current flowing through the standard resistance.
In the practical form the potentiometer wire is partly replaced by a number of coils of wire, say 14 (see fig. 1), and the potentiometer wire itself has a resistance equal to one of these coils. One terminal of the galvanometer can then be shifted to the junction

Fig. 1.
between any pair of consecutive coils and the slider shifted to any point on the potentiometer wire. By such an arrangement the potential difference can be measured of any amount from 0 to 1·5 volts. In some cases the potentiometer wire is wholly replaced by a series of coils divided into small subdivisions. We may employ such a potentiometer to measure large potential difference greater than the electromotive force of the working battery, as follows: The two points between which the potential difference is required are connected by high resistance, say of 100,000 ohms or more, and from the extremities of a known fraction of this resistance, say, 1/100 or 1/1000 or 1/10,000 wires are brought to the potentiometer and connected in between the slider and the corresponding galvanometer terminal. We can thus measure as described the drop in volts down a known fraction of the whole high resistance and therefore calculate the fall in potential down the whole of the high resistance, which is the potential difference required. The potentiometer and the divided) resistance constitute a sort of electrical scale yard by means of which any electromotive force or difference of potential can be compared with the electromotive force of a standard cell. Very convenient and practical forms of potentiometer have been devised by Crompton (fig. 2), Nalder, Elliot Bros., Fleming

Fig. 2.—Diagram of the Internal Connexions of a Crompton Potentiometer.
a b, The scale wire.
c, The set of equal potentiometer coils in series with it.
d, The double pole switch connecting the 6 pairs of terminals A B C D E F in succession to the slide contacts.
e, The resistance coils.
f, The rheostat.
g, The galvanometer key.
A, B, C, D, E, F, Terminals to which standard cell or voltages to be tested are attached.
and others. An essential accompaniment therefore of the potentiometer is a series of standard low resistances, say of 0·1, 0·01, 0·001 ohm, and also a series of higher resistances divided into known fractions. In practical work, the low resistances take the form of certain strips of metal which have on them two pairs of terminals, one termed "current terminals," and the other "potential terminals." These resistance strips, as they are called, are carefully adjusted so that the resistance between the potential terminals has a known low value. In order to measure the value of a continuous electric current, and therefore to calibrate any ampere meter we proceed as follows: The ampere meter is placed in series with a suitable low resistance strip, say of 0·01 ohm. From the potential terminals of the strip, wires are brought to the potentiometer so as to determine their potential difference in terms of the electromotive force of the standard Clark cell. An observation is then taken of the reading of the ampere meter and of the fall of resistance down the low resistance when a certain steady current is passing through the strip and ampere meter. Supposing that the potential fall down the strip is found to be ·981 volt, the strip difference having a resistance of 0·1 ohm, it would be seen that the current passing through the strip was 98·1 amperes. If then the ampere meter Scale reading was 100 it would show an error of that scale reading of minus 1·9 amperes or nearly 2%. In the same manner the potentiometer may be used to calibrate a voltmeter by the aid of a divided resistance of known value.
In electrical measurements connected with incandescent electric lamps the potentiometer is of great use, as it enables us to make accurately and nearly simultaneously two measurements, one of the current through the lamp and the other of the potential difference of the terminals. For this purpose a resistance, say, of one ohm is placed in series with the lamp and a resistance of 100,000 ohms placed across the terminals of the lamp; the latter resistance is divided into two parts, one consisting of 1000 ohms and the other of 99,000 ohms. The potentiometer enables us to measure therefore the current through the lamp by measuring the drop in volts down a resistance in series with it and the potential difference of the terminals of the lamp by measuring the drop in volts down the 100th part of the high resistance of 100,000 ohms connected across the terminals of the lamp.
Standard Cells.—A necessary adjunct to the potentiometer is some form of standard cell to be used as a standard of electromotive force. In the case of the Clark standard cell above mentioned the elements are mercury and zinc separated by a paste of mercurous sulphate mixed with a saturated solution of zinc sulphate. Other voltaic standards of electromotive force are in use, such as the Weston cadmium cell, the Helmholtz calomel cell, and the standard Daniell cell. The Clark cell is made in two forms, the board of trade or tubular form, and the H form of cell devised by Lord Rayleigh. The German experts seem to favour the latter form; the specification issued by the Physikalisch-Technische Reichsanstalt of Berlin may be found in the Electrician, xxxi. 265-266. The electromotive force of the cell diminishes with rise of temperature, the board of trade value being 1·434 volts at 15° C.[1] and 1·434 (1−0·00077 (t−15)) volts at t° C. A more exact expression is obtained if instead of 0·00077 the quantity 0·000784+0·000017 (t−15) is used. In the Weston standard cell cadmium and cadmium sulphate are substituted for zinc and zinc sulphate; it has the advantage of a much smaller coefficient of temperature variation than the Clark cell. It is most conveniently made up in a glass vessel of H form, pure mercury and cadmium amalgam being the two elements (fig. 5), and when made as directed below it has at t° C. an electromotive force Et volts, such that
E = 1·0184−0·0000406 (t−20)−0·00000095 (t−20)2+ 0·00000001 (t−20)°.
After the platinum wires have been sealed through the glass, a little aqua regia is placed in the cell legs until bubbles of gas arise from the platinum, when it is thrown out and replaced by a solution of mercurous nitrate. Then, by the use of another piece of platinum as anode, mercury is electrolytically deposited upon the platinum, which may also be amalgamated by making it white hot in a Bunsen flame and plunging it in mercury. To prepare the cadmium amalgam, one part of pure cadmium is dissolved in six parts of pure mercury, and the product while warm and fluid is placed in one
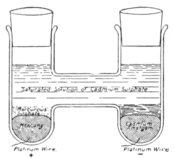
Fig. 3.—Lord Rayleigh’s H form
of Standard Voltaic Cell.
limb of the cell and warmed, to ensure perfect contact with the platinum wire. The cadmium sulphate solution is prepared by digesting a saturated solution of cadmium sulphate with cadmium hydroxide to remove free acid, care being taken not to raise the temperature above 70° C., and then by digesting it still further with mercurous sulphate until no more precipitation occurs. The cadmium sulphate solution must be saturated and have free crystals of the salt in it. The mercurous sulphate must be free from acid, and made neutral by trituration with finely divided mercury. In making the paste, so much cadmium sulphate must be added that a saturated solution of that salt is formed and is present in the cell. The cell has the electromotive force above stated if the amalgam of cadmium has from 6 to 13 parts of mercury to 1 of cadmium. The German investigators seem to have a great preference for the H form of cell, but it is clear that a narrow tubular cell of the British board of trade form not only comes more quickly to the temperature of the water bath in which it is placed, but is more certain to be wholly at one temperature. In a modification of the H form devised by F. E. Smith, of the National Physical Laboratory (Phil. Trans., A, 207, pp. 393–420), a contraction formed in the side of the vertical tube tends to hold the contents in place. Fig. 4 shows this cell, hermetically sealed, mounted in a brass case.
In cases when great accuracy is not required, a Daniell cell can be used as a standard of electromotive force. The form designed

Fig. 4.—Method of mounting
Weston Normal Cell.
Brass case removed.
by J. A. Fleming (Phil. Mag., 20, p. 126) consists of a U tube, one leg of which contains a rod of pure amalgamated zinc, and the other a rod of freshly electrotypes copper. The legs are filled with solutions of zinc sulphate and copper sulphate, the zinc rod being in the zinc sulphate and the copper rod in the copper sulphate. When so made, the cell has an electromotive force of 1.072 volts and no sensible temperature variation. The solutions are made by dissolving the purest recrystallized sulphate of copper and sulphate of zinc in distilled water. For the zinc solution, take 55.5 parts by weight of crystals of zinc sulphate (ZnSO47OH2) and dissolve in 44.5 parts by weight of distilled water; the resulting solution should have a specific gravity of 1.200 at about 20° C. For the sulphate of copper solution, take 16.5 parts by weight of pure crystals of copper sulphate (CuSO45OH2) and dissolve in 83.5 parts by weight of water; the resulting solution should have a specific gravity of 1.100 at 20° C. The solutions should be adjusted exactly to these densities and kept in stock bottles, from which the reservoirs of the cell should be filled up as required. A form of potentiometer employing a vibration galvanometer and suitable for alternating current measurement by null methods has been devised by Dr Drysdale (see Proc. Phys. Soc. Lond. 1909, 21, 61.)
See J. A. Fleming, Handbook for the Electrical Laboratory and Testing Room, vol. i. § London, 1903)—vol. i contains on pp. 108–110 an extensive list of various original memoirs published on the Clark and Weston cells; G. D. Aspinall Parr, Electrical Engineering Measuring Instruments (London, 1903); W. C. Fisher, The Potentiometer and its Adjuncts (London, 1906).
- ↑ According to K. Kahle and W. Wien, the electromotive force of the H form of Clark cell is 1·4322 volts at 15° C.
