A Voyage in Space/Lecture I
A VOYAGE IN SPACE
LECTURE I
THE STARTING-POINT, OUR EARTH
The idea of a "Voyage in Space" is not new by any means. Two thousand years ago it occurred to the Greek writer Lucian to suppose a man flying up to the heavens. He called him Icaro-menippus, because Icarus was supposed to have been the first man to fly. In one of the old stories which were told to Greek children (just as stories are still told to children even in our twentieth century), it was related how Daedalus, the father of Icarus, made him some beautiful wings; but they were only fastened on with wax, and when Icarus flew near the Sun, the wax melted and he fell. Lucian's Icaromenippus was wiser. He caught a large eagle and a large vulture; and then he relates how
He practised flying, gently at first, and then more boldly, until he flew up to the Moon, and looked down on the Earth (see Frontispiece), which he declared was much smaller than the Moon. One of the striking points in Lucian's tale is the suggestion that the eagle's wing endowed Icaromenippus with the eagle's sight.[I]cut off very carefully the right wing of the eagle and the left of the vulture, then tied them on, securing them over the shoulder by strong straps, and at the ends of the quill feathers I put in things like loops for my hands to grip.[1]
An eagle has the keenest sight of any living thing, and the eagle alone looks straight at the Sun.
And so he was able to see things happening on the distant Earth.
Nowadays, of course, we should bring a telescope into the story; but the telescope was not invented until more than a thousand years after Lucian's time, and the best he could think of was this vague notion of the eagle's "strong sight," which in some mysterious way helped Icaromenippus to see very distant things. But since he had not the magnifying power of a telescope the distant things looked very small. He tells how our earthly cities, "including the inhabitants, were not at all unlike ant-hills." It is good for us sometimes to remember how small we are compared with the universe, or even with the solar system of which our Earth is a rather unimportant member: and it is noteworthy that in this early example of a pretended "Voyage in Space" Lucian does not forget to make this use of it.
Since his day many others have had the same notion of pretending to get away from the Earth, and to visit one or other of the planets.
In my boyhood we read a book by Jules Verne, in which a projectile carrying three men is supposed to be shot from an enormous cannon towards the Moon.[2] The pictures were fascinating, and it is distressing to find that the edition with the pictures seems to be out of print; at any rate, I have not been able to recover a copy, though I much wanted to reproduce some of the pictures for you on the screen. There was a terrible explosion when the cannon was fired, and how those poor men ever survived the shock is a mystery which only great writers like Jules Verne can understand. But they did survive, and had most wonderful adventures. They even had the complacency to go over their calculations again, while inside their projectile, travelling at a furious speed towards the Moon; and found that they had made a mistake! It was rather late to find it out, wasn't it? after they had started all wrong. It is better to go over such calculations twice before one commits one's safety to them; but if these particular people had done so, we should perhaps not have had such a good story. The result of the mistake was that they never reached the Moon at all, but circled round it; and by an ingenious device they ultimately came back to Earth. I hope you will read all their adventures for yourselves.
In recent times, Mr. H. G. Wells has written about a supposed visit to the Moon, called The First Men in the Moon. He had not quite the courage to explode his travellers out of a huge cannon like Jules Verne, and so he invents a curious material called Cavorite, which screens off gravity (we shall have a good deal to say about gravity in a moment). Mr. Wells relates how a car, covered with this strange material, can rise quite smoothly from the Earth without the fearful explosion: and the occupants of the car are thus able to reach the Moon, where they find that the inhabitants are like insects rather than like us men and women: and though they are smaller and weaker than we are, their cattle—their "moon-calves"—are immensely greater than ours. There are plenty of exciting adventures in this book too, and Mr. Wells has tried to keep as nearly as he can to what is possible, according to such information as our telescopes give us about the Moon. Of course, his "Cavorite" material is as yet quite unknown—we have not even an inkling of an idea how to screen off gravity; but if we agree to make him a present of this rather startling notion, he uses it very skilfully to pilot his readers through varied experiences. Such books as those of Verne and Wells are worth reading, not only by a "juvenile audience" such as this, but by astronomers too: it is a most useful lesson to them to try and specify exactly where the author is keeping within the possibilities, and where he is making a real mistake. Let me mention one more of such books which I have read with keen pleasure—A Honeymoon in Space, by Mr. George Griffith. I think you can buy it for sixpence, and it teaches us a lot of astronomy in very pleasant fashion, because we have not the idea of lessons in our minds when reading it; and it is much nicer to avoid lessons if we can. I am afraid I shall not be able to avoid the appearance of giving lessons so skilfully as Mr. Griffith or Mr. Wells, because for one thing I am not going to attempt to tell a connected story as they have done. What I shall endeavour to do is to bring before you some of the difficulties of making such voyages, so that you may understand as clearly as possible how they arise: which of them we may hope to get rid of in time, and which seem beyond our powers. And we shall begin to-day with the first difficulty of getting away from this Earth at all.
Why is it so difficult to get away? If we jump up we come down again. We call the reason "gravity," and sometimes we are tempted to let the matter rest when we have given a name to the difficulty. But I want us to think a little more about it than this: to think about what the nature of it is, and also about the great men who found out for us what gravity is. Because it took a great deal of finding. About 2000 years ago, in Greek times, they had some curious ideas about it. The great Greek philosopher Aristotle said that if you took a light thing and a heavy thing and dropped them together, the heavy thing fell much faster. Here are his actual words; some of you (very few, I hope) may not be able to read Greek, and so we will translate them; but it is better to show you the actual words that Aristotle used, because what he said seems so strange to us now.
ὁρῶμεν τὰ μείζω ῥοπὴν ἔχοντα ἤ βάρους ἤ κουφότητος, ἐὰν τἆλλα ὁμοίως ἔχῃ τοῖς σχήμασι, θᾶττον φερόμενα τὸ ἴσον χωρίον, καὶ κατὰ λόγον ὃν ἔχουσι τὰ μεγέθη πρὸς ἄλληλα.
"We see that bodies which have a greater tendency of heaviness or lightness, if they are otherwise similar in shape, pass more quickly through the same space, and in the ratio which the magnitudes have to each other."
What it comes to is this, that if you have a ten-pound weight and a one-pound weight and you drop them together, the ten-pound weight will fall ten times as quickly. The magnitude of the weight settles how quickly it shall fall. That seems to us so astonishing that we can hardly imagine that any one believed it. Yet people went on believing that for 2000 year—just because Aristotle had said it.
Now is it better to believe things people tell you, or is it better to try and find out for yourselves? That is about the hardest question to answer that can be set. At first sight it seems better to believe what people tell you. They may tell you, for instance, that fire burns; and so you need not put your hand in the flame to find out. Or they may tell you that something is poisonous; and if you believe what you are told, you avoid eating it and continue to live. If on the other hand you persist in trying for yourself, you may die; and there is the end of trying things. In this way we seem to have answered our question pretty easily: it seems far better to believe what you are told, because you get all the advantages of other people's experience: and perhaps if they would confine themselves to telling us what they had actually tried, we might be satisfied with this answer.
Unfortunately, however, we cannot always be sure that people are speaking from experience: sometimes we are quite sure that they are not; for instance, we are sure that Aristotle had not tried the experiment of dropping two different weights; if he had, he would have written something very different. Yet he was believed because he wrote so confidently, and because people had a great respect for him in other ways, and perhaps most of all because we are taught in childhood to believe what we are told. The boy who likes to try things for himself is regarded as a troublesome and naughty boy, and is apt to get a whipping, even if he does not get burnt or poisoned. Yet the world has good reason to be very thankful to some of these naughty boys who have persisted in trying things for themselves.
Galileo was one such, and came in for punishment at the time: here on the screen you see a copy of a fine picture in the gallery at Cologne showing his punishment in prison. His troubles began when he first questioned this statement of Aristotle that a ten-pound weight would fall ten times as quickly as a one-pound weight, and by his trying the experiment for himself he first threw some light on this problem of gravity—the force which prevents our getting away from the Earth. Galileo was born at Pisa, a little town in the north of Italy, famous for its leaning tower. He went to school at Florence, not far away; and was determined to become a professor of mathematics. Several times he seemed to have a good chance of such a position, and was disappointed; but ultimately, to his great delight, he was elected Professor at his native city of Pisa, and he made use of the leaning tower to try his famous experiment with a ten-pound weight and a one-pound weight. In the presence of many witnesses, who had all pinned their faith on Aristotle, he dropped the two weights together; and they struck the ground together, showing that Aristotle's statement was quite wrong. Even then—such is the reluctance to abandon an old idea—people would not believe
the thing they saw with their eyes. Such was their profound respect for Aristotle that they declared that there must be some mistake in the experiment, since Aristotle could not be wrong.
In honour of Galileo's memory, I want us to try this experiment to-day, as well as we can. We have no leaning tower, but the roof of this building is pretty high: we have no Galileo, but some one has kindly offered to represent him, and he will drop these two balls, a wooden one and a leaden one, from the roof overhead into this box of sand, so that we may see for ourselves whether they fall together or not. There! you see they fall together just as they did 300 years ago from Pisa's leaning tower. Perhaps you may think that Galileo's representative did not drop them quite fairly together? That is quite possible, though I feel sure he tried to do so; but to make quite sure of being fair we have arranged a kind of trap for the balls up aloft which can be worked from below by means of this long string, which perhaps one of the audience will pull for me.
There again! they have fallen, you see, quite together; and do you see that the wooden one is lying on the top of the sand while the leaden one has quite disappeared? It is buried so deep in the sand that it is quite difficult to find it. This fact does not concern us very much at the moment, though it is interesting as showing the different weights of the two balls; but when we come to speak of meteorites in the next lecture, we shall find it useful to remember how a body striking the Earth may bury itself deeply. A very great man, Charles Darwin, used to say that we ought to learn all we can from an experiment, whether it is of immediate importance or not: and this tendency of heavy falling bodies to bury themselves in the earth is just such an extra consequence as he would have delighted to note.
But to return to the main point; there may have been, perhaps, a little difference between the times of the two balls: indeed there certainly was, and we know the cause of it. It is the resistance of the air, which acts more effectively on light bodies than on heavy. For two solid balls such as we have used the difference is not great: but if we took a feather or other very light body we know that it would fall very slowly. This does not mean that gravity acts less on a feather than on a piece of lead, but that the air resists its fall more effectively. If there were no air, the feather would fall just as quickly as the balls of wood and lead. I cannot show you this by exhausting all the air from this room, because we want some of it to breathe, but if you will kindly be content with a much smaller drop, we can do the experiment with this tall jar. It is an experiment which has been done many times before and is called the "coin and feather" experiment. The coin used to be a golden guinea, but I fear none of my audience is likely to have such a coin with them, and perhaps they might not even like to lend me a sovereign, so I must use one of my own. We put a feather alongside it in a little trap, rather like that which released the balls, and then we close the tall jar over them and exhaust all the air. In old days this was done with a hand-pump, and required some exertion, but with the beautiful resources of this Institution we have merely to attach a tube and turn a tap; in a few seconds we have a nearly perfect vacuum. And now, if we release the trap, you see that the coin and feather fall together. Directly we turn the tap again and let the air in, the feather blows about while the coin rests stolidly at the bottom. Here, again, is a thing worth noting that is not immediately before us—this rapid inrush of the air from outside into the exhausted space. If the jar had been full of air and the outside empty the rush would of course have been the other way and would soon have left very little in the jar. Now in Jules Verne's book, of which I spoke early in the lecture, the brave men who went in the projectile took with them a dog, and the poor dog died. They thereupon opened a trap-door and put it outside; but I fancy this would have been much more difficult and dangerous than Jules Verne thought, because though the travellers had taken the precaution to carry plenty of air with them inside their projectile, there would be very little outside it when once they had got some distance from the Earth. We shall see in the next lecture how very shallow our atmosphere—is the projectile would pass right through it in a few seconds. Hence, when the trap-door was opened to put out the body of the poor dog, I fear all the air would have rushed out almost at once, and the men would have died too, and so would the story.
If we want the story to go on, we must let Jules Verne tell it in his own way: but there is no harm in making mental reservations, and we will take the opportunity to make one more, because it brings to our notice another fact about Gravity, in which we are specially interested to-day.
We have already said that when we jump up we come down again because of Gravity—because the Earth pulls us to itself. Now when Jules Verne's travellers opened the trap-door and put the poor dog out—probably with a fairly good push, because they would be in a hurry not to let more air escape than they could help—when they pushed the dog away from the projectile, would it fall back again on to the projectile as we fall back on to the Earth when we push ourselves away by jumping? We know that the Earth pulls things to itself, but do other bodies also pull other things to themselves in the same way? We can scarcely believe that they do because we never feel the pull of anything but the Earth. If I stand near an object such as this desk in front of me I do not feel any pull towards it, and yet, as a matter of fact, it is pulling me and so is everything else in the room, though the pulls are too slight for me to feel. That is one of the laws of Gravity, that everything is pulling or attracting everything else; but the amount of pull or attraction depends firstly on the size of the body that pulls, and secondly on its distance away. The great Sir Isaac Newton first proved these laws some 250 years ago, and we will presently recall how he did it, just as we have recalled Galileo's experiment to memory. But for the moment I only want you to notice one point—that a large body like our Earth exerts a greater pull than a small one like this desk or like the projectile from which Jules Verne's travellers pushed the dog. Undoubtedly the projectile would try to pull the dog backwards, but owing to its small size it might not succeed, and then the dog would go farther and farther away. We cannot tell what would happen without knowing how hard the dog was pushed out. If a thing is pushed hard enough it can get away even from the Earth—indeed, that is exactly the point of Jules Verne's story, how a very hard push, from a huge cannon, sent the projectile right away from the Earth. The push had to be very hard indeed because the Earth is so big that it pulls very strongly: the pull of the little projectile would be very feeble indeed so that even a very slight push would send the dog right away, never to fall back. This, however, is not what happens in the story: the dog neither goes right away nor falls back, but goes round and round the projectile as a "satellite," that is, as our Moon goes round us: and here I am sorry to say Jules Verne makes another mistake, though it would take too long to explain why. Let us be satisfied for the moment to notice this great fact that a large body pulls harder than a small one. Perhaps you think that is not surprising, perhaps it seems natural to expect more from a large body. Let me remind you that it was just by following what seemed natural that Aristotle made his big mistake: it seemed to him natural to expect a large body to fall quicker than a small one, and he was wrong, as Galileo proved by trying it. If I had no better reason than that it seemed natural, I should not ask you to believe that a large body pulls harder than a small one; but there is a much better reason, namely that the experiment has been tried many times.
One famous experiment was made in 1798 by Henry Cavendish (of the same family as the Dukes of Devonshire), but it is by no means the only one: the experiment is really being made by astronomers every day, for if the fact were not true none of their calculations would come right as we know they do.
Well, then! we may accept this fact that all bodies, even the tiniest little particles, are pulling as hard as they can, though particles cannot do much. It is only when a great crowd of them are massed together to make the Earth that the pull becomes easy to feel. And when we get an enormously greater crowd still, such as the Sun, the pull is enormously greater. Why, then, does not the Sun pull us away from the Earth? Well, there is more than one reason; but one at least is that he is so much farther away, and this brings us to the next fact we have to notice about Gravity—that it depends on the distance.
A body close to you pulls hard: take it farther away and the pull becomes less. Mathematicians say that it diminishes as the "inverse square of the distance"; but we can put the law into simpler language in this way. Take a body twice as far away, and the pull is one quarter of what it was; bring it twice as near, and the pull is four times what it was. And now let us go back to the history of the discovery and see how Newton found this out for us.
About the time when Galileo lived in Italy, there was another wonderful man called Tycho Brahe, living in Denmark, who also mistrusted some of the things told him on good authority. For instance, there were books giving the positions in which the planets ought to be seen at any time, which were still trusted although the planets could be seen not to follow the books. Tycho determined to go to work for himself, observing carefully the movements of the planets with the idea of making better books or tables than those in use. A beautiful observatory was built for him on the little island of Hveen, and he called it Uraniborg—Heavenly City—because it was devoted to the study of the heavens. Kings and nobles visited him there out of respect for the
great work he was doing: and he himself had such reverence for it that whenever he observed the stars and planets he put on his richest robes. The telescope had not yet been invented, so that his observations were made by the use of "sights" such as are used on rifles—a "back"-sight near the eye, and a "fore"-sight at the further end of a straight bar pointed towards the star. Compared with what we can now do with a telescope the observations were rough indeed; and yet they were the means by which we learnt the laws of Gravity. This, however, was not until many years after Tycho Brahe himself was dead: he made thousands of observations, but
A Sextant used by Tycho Brahe.
did not live to find out all they could tell him. Fortunately he had a devoted pupil, Kepler, a German, who went on working at them, and found out the very important things they showed. Kepler is represented with a pair of compasses in his hand, showing that he was fond of measuring things, which is really the chief business of an astronomer—not merely looking at the stars and planets, but measuring their distances apart, or something else that can be measured. Tycho Brahe was also animated by this devotion to measurement, otherwise Kepler would not have been able to use his work as he did. By use of it he found three great laws of movement for the planets. No one suspected the simple laws of Gravity as yet, but Kepler made it possible to find them by establishing the three great laws of movement which have ever since been called by his name —Kepler's Laws. The first is that the planets move round the Sun in ellipses. You can easily draw an ellipse for yourself with two drawing-pins and a loop of string. Fix the pins in a
drawing-board and put the loop of string round them, keeping it stretched into a triangle with a pencil point. You can still move the pencil about and it will draw you an ellipse. The drawing-pins are called the foci of the ellipse, and when a planet moves in an ellipse the Sun is at one of the foci. Once when the late Sir Robert Ball (who several times gave these Christmas lectures) had mentioned this fact that the Sun occupies one of the foci of the ellipse, he was earnestly implored by a lady after the lecture to tell her which of the foci was the one. I am afraid I should have tried to explain that it did not really matter, and the explanation might have taken a long time. But Sir Robert was cleverer than that: raising his right hand, he said, "Madam! the right
one" (which of course was right in any case), and the lady thanked him warmly and went away quite satisfied. But whichever focus we choose it will be nearer one end of the ellipse than the other. Now Kepler's second law tells us that the planet moves quicker when it is near the Sun than when far away. He put it into more precise form, but that will be enough for us to remember—that when a planet or comet is near the Sun, it bustles along at a great pace, when it is far away it moves more soberly, and when very far away it loiters terribly. That is really because the gravity or attraction of the Sun is feeble at a distance and strong when close; but Kepler did not quite realize about this attraction, he contented himself with noting that the planet moved more slowly or more quickly. And finally he found a third law, which is rather tiresomely
(See Notes to Illustrations.)
mathematical at first sight, but was the most important of all for taking the next step, and therefore we should pay it some attention.
It states that if a planet be placed at a distance from the Sun 4 times as great as that of our Earth, it will take 8 times as long as we do to go round the Sun completely, that is to say, 8 years; and if it is 9 times as far away, then 27 years; if 100 times as far away, then 1000 years. Can you see how these numbers are related? Please look carefully at
| Simple Number |
Square for the Distance |
Cube for the Time | |||||
| 1 | 1 × | 1 = | 1 | 1 × | 1 × | 1 = | 1 |
| 2 | 2 × | 2 = | 4 | 2 × | 2 × | 2 = | 8 |
| 3 | 3 × | 3 = | 9 | 3 × | 3 × | 3 = | 27 |
| 4 | 4 × | 4 = | 16 | 4 × | 4 × | 4 = | 64 |
| 10 | 10 × | 10 = | 100 | 10 × | 10 × | 10 = | 1000 |
this little table. Four is called the square of two, because if one square is twice as long and twice as broad as another, it is four times the first in size. We are almost reminded of the Red Queen's argument with Alice, "Five times as warm and five times as cold—just as I'm five times as rich as you are and five times as clever." Poor Alice gave it up like a riddle with no answer: but we must not give it up here, we must go even a step further. When one thing is twice as long and twice as broad and twice as high, we go beyond the square to the cube.
If we multiply 2 × 2 × 2, we get 8, which is the cube of 2: and when the distance is the square of a number, the time is the cube of the same number.
None of the planets fits these numbers exactly: there is no planet at 9 times the Earth's distance, but Saturn is at 10 times—just a little bigger than 9—and we can therefore see from the table that it will take rather more than 27 years to go round the Sun (29½ years as a matter of fact). But we need not trouble about the exact figures if we understand the principle of this great Third Law of Kepler.
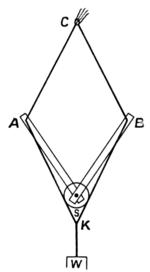
On that law Sir Isaac Newton and others went to work, and soon saw that it told them the Law of Gravity. You have heard the story of Newton and the apple, which must surely be true, because here is a bit of the actual apple tree from Newton's garden at home: it now belongs to the Royal Astronomical Society and they have kindly lent it to us for this occasion. In the entrance hall you will find a beautiful picture of Newton under the apple tree, thinking about Gravity. But though the story of the apple may be quite true, it may suggest to you what is not true, namely, that he thought out the law of Gravity very quickly after seeing the apple fall. This was not the case: it took him 20 years to work out the great law fully in all its bearings. When he saw the apple fall, he began to think; he wondered if the pull of the Earth which made the apple fall, and which brings us down again when we jump up, would still be the same if we could go farther away, or how it would alter; and his thoughts took him farther and farther away till he thought of the Moon, and whether it was feeling the pull of the Earth. And then he must have thought of the movement of the Moon and of other bodies in the heavens, and naturally he would think of Kepler's three laws: and then the third of them, which we have just been talking about, led him to see that if the movements of the planets were in any way controlled by a pull from the Sun, the pull must be weaker at a distance, and stronger close to the Sun: and he calculated how much stronger it would be. Instead of stating the law in the language he used, let us illustrate it with this piece of apparatus, because it is easier to understand a thing when we have something to look at. You can easily make the apparatus for yourselves. Take two equal wooden bars SA and SB (Fig. 2) and put a screw through them at S, into the side of a ladder. The holes in the bars should be larger than the screw shaft so that they will turn freely. At A and B tie the ends of two exactly equal cords ACB and AKB. To the middle (K) of one of them hang the weight W, and hold up the other
Fig. 2.
Now when you go up the ladder and hold C high up, as in Fig. 2, you will find that it is quite easy to support the weight W perhaps with one finger. You may have to ask some one to lift up the weight for you in the first instance, but once lifted, it is very easy to hold it up. If a pair of reins were made on this principle, a child could hold back a runaway horse.
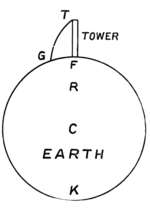
But now drop C down to halfway so that the bars open out. You will find that the pull is much greater—four times as great, as Newton tells us. It is not very strong even yet, but it is beginning to be felt. Here is a spring-balance with which we can measure the pull at C, and you will see that the spring is scarcely moved. If again I let C (the comet) come twice as near to the Sun the pull is four times as great again, or sixteen times as great as at
Fig. 3.
Fig. 4.
The rotation of the Earth can indeed be shown in this way, as Newton thought and as we will presently mention. But unfortunately Hooke misunderstood the point. His mind was full of a different problem, which had gradually come to the front as the most important scientific problem there was at the time, and which no one could solve. It was this. If gravity really changed with the distance as Newton had suspected fourteen years before, and as many others had since suspected from study of Kepler's great Third Law, then would Kepler's Second Law follow as a consequence, that is to say would the planets all move in ellipses round the Sun? People felt that probably this was a necessary consequence, but no one could prove it. Hooke claimed to have proved it, but no one now believes his claim. And he accused Newton of not knowing the fact, much less being able to prove it. This made Newton very angry. He first sat down and proved the proposition for his own satisfaction—did what every one was trying to do and could not—and then he tossed the matter aside, as he could not bring himself to reply to the disagreeable man who had wrongly accused him. And so things might have remained had it not been for Edmund Halley, a man of a very different kind, who came in the nick of time to rescue this great achievement of Newton's. Halley was an Oxford man, Newton was at Cambridge: Oxford and Cambridge often meet in friendly rivalry, but this time they met in co-operation, and took each a share in the great discovery of Gravity, though the share of Cambridge is of course much the greater. Halley had tried without success to get an answer to the difficult question whether planets moved in ellipses because the Sun attracted them in the way suspected; and as a forlorn hope he travelled all the way to Cambridge to ask Newton about it. To his great delight, Newton replied that he had proved the proposition completely; though oddly enough he could not find the paper on which he had written it out. Newton was not careful and tidy, as we all are, I hope. But he was very, very able: and soon wrote out a new proof and sent it to Halley, who had already hastened to London to tell the Royal Society the good news that the great problem was solved. This was, however, rather premature exultation, though no one suspected it but Newton. He knew that there was still the formidable difficulty we have noticed: he had not yet found out where to measure the distance from, whether from the nearest point of the Earth (or other attracting body) , or its centre, or some other point. But so much had he been stimulated by Halley's visit and genial influence, that he forthwith attacked this difficulty again, this time with success: he found the astonishing result that you must measure always from the Earth's centre.
We may therefore summarize the history of this great discovery in three steps—
(i) In 1665 Newton saw the apple fall, and was led to think of the Law of Gravity: "the attraction is inversely as the square of the distance." But he could not see how to measure the distance accurately.
(ii) In 1679 he made the suggestion of proving the Earth's rotation; and Hooke's reply irritated him into solving "the problem of the ellipse"; the solution, however, he kept to himself.
(iii) In 1685 Halley's visit elicited the solution and stimulated Newton into finding that the distance must be measured from the centre of the attracting object.
You see what an important crisis it was when Newton suggested his experiment for proving that the Earth rotates: and in honour of him we will now make such an experiment, though not the one he suggested. I might perhaps have shown you his very experiment, or one founded upon it: for during the last few years the rotation of the Earth has been proved and measured in this way, using, however, the apparatus known as Atwood's machine, to drop the weight. Here is a fine Atwood's machine, which has often been used in this Institution: you see two weights, one heavier than the other, connected by a string over a pulley. The heavier weight falls, pulling the other up; but the fall is comparatively slow, and can be made as slow as we please by making the weights nearly equal. Now this slow fall gives the sideways "flick" due to the Earth's rotation plenty of time to develop. When the experiment is made just as Newton described it, the fall is so rapid that the "flick" has scarcely time to work: with Atwood's machine, it gets a much better opportunity. And where do you think this ingenious development of Newton's idea has been put into practice and the rotation of the Earth demonstrated and measured? Why! at the observatory of the Vatican, where 300 years ago things were made so unpleasant for Galileo merely because he asserted this rotation. Truly Time brings changes!
But this beautiful method of Father Hagen is perhaps not the easiest way for us to see the rotation of the Earth within a few minutes. We had better use the method of an ingenious Frenchman called Foucault, who used for the purpose a long pendulum like this. If you swing a pendulum truly backwards and forwards, without any wobble, it will go on swinging in the same way even though the Earth rotates underneath it. Here is a little pendulum mounted on a model earth: I set it swinging and turn the model earth round—the pendulum still goes on swinging in the same way: it takes no notice of the rotating Earth underneath, though I have turned the model a quarter turn (so that if the pendulum went with it, the swing would be at right angles to its former direction). If, however, there were people living on this model earth, they would not be conscious that I had turned it round: to them the pendulum would seem to change: to them it would seem to be swinging now at right angles to its former direction. And so our long pendulum will not really change, but will seem to us to be changing. But to turn our actual Earth a quarter round takes six hours: we should have to go home to tea long before that: we must be satisfied to watch the real pendulum for a few minutes only. Nevertheless we can see its apparent change if we magnify it in the ingenious way devised by Sir James Dewar.
Here is the pendulum tied back. Presently I am going to swing it by burning this string which ties it up. When the string breaks in burning, the pendulum will swing backwards and forwards. At one end of the swing it comes very close to this lamp which is throwing the shadow of the pendulum-wire on the screen, and you will then see the wire and the motion much magnified; so that we can easily tell whether the swing changes even a little bit. But it is not the pendulum that is changing, it is the Earth rotating underneath; and in a minute or two we shall see the effect of the earth moving.
[In Fig. 5 the pendulum bob was at first swinging from D to C; the shadow being thrown on the screen from the point X was near the middle of the screen most of the time, but as the pendulum bob reached the point C, the shadow fell at c, away to the right. Presently the earth's rotation altered the path of the bob to BA, and at A the shadow fell at a, away to the left.]
FIG. 5. FOUCAULT'S PENDULUM.
Magnification of the Effect.
You will see that as the pendulum comes up to the lamp the shadow will flash to the right, and it would go on doing that always if the earth did not move; but as the earth moves it will presently go to the left. There will be a moment when it will spread out on both sides; and after that it will go to the left. I hope we can manage the experiment without keeping you too long. Now I will burn the thread. There, you see it goes to the right, and presently it will go to the left. You remember when Peter Pan asks those who believe in fairies to clap their hands? Well, I don't want you to believe in things you do not see, but when you see the Earth rotating, that is, when the shadow goes to the left instead of to the right, then you clap your hands; for then you will have seen the rotation of the Earth. Surely it is beginning to go over now, it is more to the left than to the right! (The audience here testified as requested.) In this way you can soon see the Earth rotating, if the experiment is carefully prepared beforehand.
There is another way in which it has been shown by M. Foucault that the Earth is rotating. He showed it by means of a gyrostat. He spun a top quickly and set it up in a certain position. Now a thing that is spinning has got a great tendency to remain in the same position. For instance, we know that a spinning top does not fall down, though it may turn round. I cannot show you M. Foucault's exact experiment, but I can show you some pretty things of the same kind which tell us as much as we want to know. Perhaps you have played with gyrostats already: but probably you have wound them up with string; Mr. Gray, of Glasgow, has invented some beautiful gyrostats which are wound up by means of a small motor. Here is one now spinning very quickly, and if I put it horizontally with one end of the axis on a stand, it will not fall down, as it would if it were not spinning, but simply goes round and round. Its weight tries to make it fall, but can only make it turn round. And if we try to lift the end of the axis, we only make it turn round the other way.
That principle has been used recently for steering ships. A large gyrostat has its axis floated horizontally in mercury. If the axis points East and West, then the rotating Earth is always trying to lift the West end, but it only makes the axis turn round. And this is also more or less true for any other position except that when the axis is due North and South. Hence the axis will be always seeking that due North and South position, as the magnetic needle seeks the Magnetic Poles. This has been known a long time, but only recently has the tendency been used to make a good practical compass. This has at last been done, and the most wonderfully convincing proof of the rotation of the Earth is thus provided—we are steering ships by means of it, and entrusting thousands of lives to its efficacy.
Perhaps it will interest you to know what was the nature of the invention which has made a practical success of this compass. You have seen a workman use a plumb-line to get buildings vertical, and you know that a plumb-line is very like a pendulum. If you set it swinging it will go on swinging for some time, and be no use as a plumb-line. To bring it to rest the workman sometimes puts the bob in a bucket of water, which quickly stops the swinging. This kind of stopping is called "damping" the swing, though it has nothing to do with the water wetting the bob; it merely means that the inconvenient swinging is stopped. Now when a gyro-compass is set up, unless it is pointed exactly North from the first (which is unlikely), it will swing to and fro to find the North, just as a plumb-bob swings to and fro to find the vertical. But the swinging of the gyrostat will be much slower and more persistent than that of the pendulum—so slow and so persistent that most people thought it impossible ever to bring it to rest. But some ingenious Germans have actually found a way, and their invention (which corresponds to the bucket of water with the plumb-bob) has made a practical success of the compass. The gyrostat in spinning round at a great rate makes air currents; and the inventors have led these air currents past a delicately adjusted metal tongue, so that any tendency to swing is resisted. Perhaps it will also interest you to hear how they came to pay attention to the matter at all. They had the notion of going to the North Pole by submarine. They thought that a boat could be sunk so as to travel under the ice to the North Pole and back. But the question arose how they were to steer. The magnetic compass would only take them to the Magnetic Pole, which is several hundred miles away from the true North Pole. The stars would not be visible from under the ice. Hence they had to think of some other plan, and it occurred to them to enquire whether they could not make use of this long-known but never-used principle of the gyrostat setting its axis North and South. Their success has been so complete that their compass is actually superior to the magnetic compass.
But we must now return to Newton and the law of Gravity. Newton proved, then, that the law of Gravity made bodies move in ellipses. An ellipse is called a conic section, because if you take a cone and cut it across you may get an ellipse. But it is not the only possible curve; you may get a parabola—a curve which does not go round and come back again, but goes on for ever. I can show you how to make a parabola, which is just as easy as to make an ellipse, I think almost easier. Take two straight lines, and set off on each a series of equal distances—let us say inches, or half inches, or whatever you like—and then join the corresponding points in the way shown in the diagram, outwards on one line and inwards on the other. I believe in some schools this is done as a needlework exercise, joining the points by threads, which shape out a parabola.
DRAWING A PARABOLA (FIG. 6.)
You need not stop at the point 8; you can go on past it, provided the lines are suitably extended, and there is no stopping-place: so you see a parabola is a curve that goes on without end. That is important to remember: for suppose we started on a journey from the Earth and moved under gravity we might get into one of these curves that goes on without end, and that would be inconvenient, for we should never get back again to Earth.
At one time it was thought that comets moved in parabolas and never came back; that they came to us once, went away and never came back at all. But soon after Newton's discovery about the law of Gravity, Halley thought he would calculate the orbits of these comets. Perhaps you have not seen a big comet, such as that which appeared in 1858.
The Great Comet of 1858.
A "comet" means a hairy star, and in old days comets were represented as stars with hair. Nowadays we get photographs of them. Anybody who has got a Kodak and can strap it to a telescope with clockwork can take a photograph of a comet.
Well, it was supposed that comets moved in parabolas, as we should if we started off with the proper velocity; and it was thought they never came back. Halley found out that they did come back, and that comets move in ellipses as other planets do, only that they are very long ellipses. It was a well-deserved reward for Halley, who took such pains to get the proof of the law of gravitation from Newton, that he should be led to this great discovery. I may add to what I have already told you, that even when Halley took Newton's great work to the Royal Society in triumph, he found to his astonishment that they were at the moment too poor to publish it. Thereupon Halley paid for it out of his own pocket, although he was not a rich man. He got his reward when he made this great discovery about comets coming back to us, and that was soon after he went back to Oxford as Savilian Professor of Geometry.
He set out to examine as many orbits of comets as he could find observations of—assuming that they went in parabolas and never came back—and he calculated the orbits of twenty-four of them. Now the calculation of an orbit is a complicated matter that I am not going to trouble you with, at present at any rate; but we can all of us understand that when figures come out the same, whatever the figures may mean, they must refer to the same thing. Look now at these figures which Halley obtained for three comets which were thought at that time to be quite different. One of them had appeared in 1531, the second in 1607, and the third in 1682; and when Halley calculated the particulars of their orbits quite separately and independently he found—
| Year of Comet |
Node | Perihelion | Inclination | Distance |
| 1531 | 49° | 301° | 18° | 0·57 |
| 1607 | 50° | 302° | 17° | 0·59 |
| 1682 | 51° | 302° | 18° | 0·58 |
The figures are not quite the same, but they are so nearly the same that if we tried to draw the three orbits we should find the pencil going over the same line as nearly as possible: and Halley immediately said that instead of three separate comets, the same one must have come three times, in the same path, which it took about seventy-six years to go round. The path must, therefore, not be a parabola, which does not admit of return, but a long ellipse. And the comet would continue to pay us visits every seventy-six years, the next visit being due in 1758. He knew that he would be dead then, but he hoped that when his words came true, the world would remember to credit an Englishman with the prophecy. Here are his actual Latin words—in those days scientific papers, intended to be read by the whole world, were written in Latin—a language all nations knew, though they might not know the language of their next neighbours.
Quocirca si secundum predicta nostra redierit iterum circa annum 1758, hoc primum ab homine Anglo inventum fuisse non inficiabitur æqua posteritas.
He was proud of his achievement, not for himself but for his nation; and that national pride is appreciated not only by us, but by other countries. My friend, Mr. Hollis, when in Paris one day, saw a picture of the supposed return of Halley's comet; he bought it, and has allowed me to reproduce it here. An angel is calling Halley from the grave to see the return of the comet, the
The Return of Halley to see his Comet
(By a French Artist.)
fulfilment of the prediction he ventured to make.
When Halley had once shown that the comet comes back every seventy-five years, it was easy to calculate when it had appeared before, and they found that it was the comet mentioned by Josephus as having appeared at the siege of Jerusalem. Josephus recorded "a fiery sword hanging over Jerusalem," which foretold its destruction. People were terrified of comets in those days, and generally associated them with disaster: and it was only when Newton and Halley showed that comets obey regular laws that this fear was dissipated. It is seldom very difficult to find some disaster which could be
Halley's Comet on the Bayeux Tapestry.
Various Positions of a Comet's Tail.
Changes in a Comet's Tail
(By E. E. Barnard.)
We thus realize that though gravity is the principal force with which we have to deal when we are travelling out into space, there are, nevertheless, other forces such as that which acts on the lighter particles of a comet's tail. I hope none of us on the journey will be blown away like the lighter particles.
The facts that the Earth rotates and that it pulls us towards itself by gravity are so familiar to us that we scarcely realize their immense importance, and it may seem strange to you to have spent so much time talking about them. But you remember the old proverb that a cow never knows the value of her tail till she has lost it. If we leave the Earth to take our voyage in space we shall lose both these things. We shall lose the Earth's rotation, and with it the changes from day to night. If the Earth stood fast as our forefathers believed, the Sun and the stars revolving round it, we should retain something of the daily change in our journey: but now we know that it is the heavens which remain still, while the Earth rotates, we must make up our minds to lose the peaceful night with its invitation to sleep. If we sleep at all, we must sleep by broad daylight, for the Sun will shine continuously when once we lose the Earth's shelter. Our watches will tell us the time, but clocks, which are driven by weights, and regulated by pendulums, will be useless when we lose the gravity that pulls the weights down and causes the pendulum to swing. It was Galileo who first found out that a pendulum kept time, and he made the discovery in the cathedral at Pisa when the lamps were lit. There was a lamp hung like a long pendulum from the roof: and the verger pulled it toward him to light it and then let it swing back. Galileo thought that as the swinging died down it would become either slower or quicker, and to test this he timed the swings with his pulse: to his amazement they were all made in the same time. He naturally tried other pendulums for himself, and found that they all had this property of keeping time though the swing may alter in size it does not alter in time. One way of realizing this property of the pendulum
Fig. 7.
Note on the Gravity Experiment
The arrangement described on p. 22 is called a "Peaucellier Cell," and can be used to draw a straight line. It was Sir G. H. Darwin who first pointed out that it could be used to illustrate gravity.
Fig. 8.
Notice that (Fig. 8)
Since KA and AS are a string and a rod of constant length, the product CS . SK is therefore constant, and it is this property which is used in drawing the straight line; for if K be made to move on a certain circle, C will move on a straight line.
As regards the use for gravity: the pull at P is to the weight W in the same ratio as the tensions in AC and AK.
Now AC is parallel to KB; and thus ALK is the triangle of forces for the point A. The ratio of the tensions is therefore that of KL to KA: or SL to SA, since KS bisects the vertical angle of the triangle: or finally SK to SC, since AC and KL are parallels.
| Thus |
In practice it is convenient to use, instead of the lower string AKB, one just half the length, attached to the middle points of the bars SA, SB: or reduced in any other ratio. The advantage gained is that S need not be so high above the ground.
- ↑ Six Dialogues of Lucian, by S. T. Irwin. Methuen & Co., 1894.
- ↑ From the Earth to the Moon (Wikisource contributor note)