54. Differentiation of
vers
v
{\displaystyle \operatorname {vers} \ v}
Let
y
{\displaystyle \ y}
=
vers
v
{\displaystyle =\operatorname {vers} \ v\ }
By Trigonometry this may be written
y
{\displaystyle \ y}
=
1
−
cos
v
{\displaystyle =1-\cos v\ }
Differentiating,
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
sin
v
d
v
d
x
{\displaystyle =\sin v{\frac {dv}{dx}}}
XVII
∴
d
d
x
(
vers
v
)
{\displaystyle {\frac {d}{dx}}(\operatorname {vers} v)}
=
sin
v
d
v
d
x
{\displaystyle =\sin v{\frac {dv}{dx}}}
In the derivation of our formulas so far it has been necessary to apply the General Rule , p. 29 [§ 31] (i.e. the four steps), only for the following:
III
d
d
x
(
u
+
v
−
w
)
{\displaystyle {\frac {d}{dx}}(u+v-w)}
=
d
u
d
x
+
d
v
d
x
−
d
w
d
x
{\displaystyle ={\frac {du}{dx}}+{\frac {dv}{dx}}-{\frac {dw}{dx}}}
Algebraic sum.
V
d
d
x
(
u
v
)
{\displaystyle {\frac {d}{dx}}(uv)}
=
u
d
v
d
x
+
v
d
u
d
x
{\displaystyle =u{\frac {dv}{dx}}+v{\frac {du}{dx}}}
Product.
VII
d
d
x
(
u
v
)
{\displaystyle {\frac {d}{dx}}\left({\frac {u}{v}}\right)}
=
v
d
u
d
x
−
u
d
v
d
x
v
2
{\displaystyle ={\frac {v{\frac {du}{dx}}-u{\frac {dv}{dx}}}{v^{2}}}}
Quotient.
VIII
d
d
x
(
log
a
v
)
{\displaystyle {\frac {d}{dx}}(\log _{a}v)}
=
log
a
e
d
v
d
x
v
{\displaystyle =\log _{a}e{\frac {\frac {dv}{dx}}{v}}}
Logarithm.
XI
d
d
x
(
sin
v
)
{\displaystyle {\frac {d}{dx}}(\sin v)}
=
cos
v
d
v
d
x
{\displaystyle =\cos v{\frac {dv}{dx}}}
Sine.
XXV
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
Function of a function.
XXVI
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
d
x
d
y
{\displaystyle ={\frac {1}{\frac {dx}{dy}}}}
Inverse functions.
Not only do all the other formulas we have deduced depend on these, but all we shall deduce hereafter depend on them as well. Hence it follows that the derivation of the fundamental formulas for differentiation involves the calculation of only two limits of any difficulty, viz.,
lim
v
→
0
sin
v
1
{\displaystyle \lim _{v\to 0}{\frac {\sin v}{1}}}
=
1
{\displaystyle =1\ }
by § 22, p. 21
and
lim
v
→
0
(
1
+
v
)
1
v
{\displaystyle \lim _{v\to 0}(1+v)^{\frac {1}{v}}}
=
e
{\displaystyle =e\ }
By § 23, p. 22
EXAMPLES
Differentiate the following:
1.
y
=
s
i
n
a
x
2
{\displaystyle y=sinax^{2}\ }
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
cos
a
x
2
d
d
x
(
a
x
2
)
{\displaystyle =\cos ax^{2}{\frac {d}{dx}}(ax^{2})}
by XI
[
v
=
a
x
2
{\displaystyle v=ax^{2}}
2.
y
=
tan
1
−
x
{\displaystyle y=\tan {\sqrt {1-x}}}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
sec
2
1
−
x
d
d
x
(
1
−
x
)
1
2
{\displaystyle =\sec ^{2}{\sqrt {1-x}}{\frac {d}{dx}}(1-x)^{\frac {1}{2}}}
by XIII
[
v
=
1
−
x
{\displaystyle v={\sqrt {1-x}}}
=
sec
2
1
−
x
⋅
1
2
(
1
−
x
)
−
1
2
(
−
1
)
{\displaystyle =\sec ^{2}{\sqrt {1-x}}\cdot {\frac {1}{2}}(1-x)^{-{\frac {1}{2}}}(-1)}
=
−
sec
2
1
−
x
2
1
−
x
{\displaystyle =-{\frac {\sec ^{2}{\sqrt {1-x}}}{2{\sqrt {1-x}}}}}
3.
y
=
cos
3
x
{\displaystyle y=\cos ^{3}x}
This may also be written,
y
{\displaystyle y}
=
(
cos
x
)
3
{\displaystyle =(\cos x)^{3}}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
3
(
cos
x
)
2
d
d
x
(
cos
x
)
{\displaystyle =3(\cos x)^{2}{\frac {d}{dx}}(\cos x)}
by VI
[
v
=
cos
x
{\displaystyle v=\cos x}
n
=
3
{\displaystyle n=3}
=
3
cos
2
x
(
−
sin
x
)
{\displaystyle =3\cos ^{2}x(-\sin x)}
by XII
=
−
3
sin
x
cos
2
x
{\displaystyle =-3\sin x\cos ^{2}x}
4.
y
=
sin
n
x
sin
n
x
{\displaystyle y=\sin nx\sin ^{n}x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
sin
n
x
d
d
x
(
sin
x
)
n
+
sin
n
x
d
d
x
(
sin
n
x
)
{\displaystyle =\sin nx{\frac {d}{dx}}(\sin x)^{n}+\sin ^{n}x{\frac {d}{dx}}(\sin nx)}
by V
[
v
=
sin
n
x
{\displaystyle v=\sin nx}
v
=
sin
n
x
{\displaystyle v=\sin ^{n}x}
=
sin
n
x
⋅
n
(
sin
x
)
n
−
1
d
d
x
(
sin
x
)
+
sin
n
x
cos
n
x
d
d
x
(
n
x
)
{\displaystyle =\sin nx\cdot n(\sin x)^{n-1}{\frac {d}{dx}}(\sin x)+\sin ^{n}x\cos nx{\frac {d}{dx}}(nx)}
by VI and XI
=
n
sin
n
x
⋅
sin
n
−
1
x
cos
x
+
n
sin
n
x
cos
n
x
{\displaystyle =n\sin nx\cdot \sin ^{n-1}x\cos x+n\sin ^{n}x\cos nx}
=
n
sin
n
−
1
x
(
sin
n
x
cos
x
+
cos
n
x
sin
x
)
{\displaystyle =n\sin ^{n-1}x(\sin nx\cos x+\cos nx\sin x)}
=
n
sin
n
−
1
x
sin
(
n
+
1
)
x
{\displaystyle =n\sin ^{n-1}x\sin(n+1)x}
5.
y
=
sec
a
x
{\displaystyle y=\sec ax}
Ans.
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
a
sec
a
x
tan
a
x
{\displaystyle a\sec ax\tan ax}
6.
y
=
tan
(
a
x
+
b
)
{\displaystyle y=\tan(ax+b)}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
a
sec
2
(
a
x
+
b
)
{\displaystyle =a\sec ^{2}(ax+b)}
7.
s
=
cos
3
a
x
{\displaystyle s=\cos 3ax}
d
s
d
x
{\displaystyle {\frac {ds}{dx}}}
=
−
3
a
sin
3
a
x
{\displaystyle =-3a\sin 3ax}
8.
s
=
cot
(
2
t
2
+
3
)
{\displaystyle s=\cot(2t^{2}+3)}
d
s
d
t
{\displaystyle {\frac {ds}{dt}}}
=
−
4
t
csc
2
(
2
t
2
+
3
)
{\displaystyle =-4t\csc ^{2}(2t^{2}+3)}
9.
f
(
y
)
=
sin
2
y
cos
y
{\displaystyle f(y)=\sin 2y\cos y}
f
′
(
y
)
{\displaystyle f'(y)}
=
2
cos
2
y
cos
y
−
sin
2
y
sin
y
{\displaystyle =2\cos 2y\cos y-\sin 2y\sin y}
10.
F
(
x
)
=
cot
2
5
x
{\displaystyle F(x)=\cot ^{2}5x}
F
′
(
x
)
{\displaystyle F'(x)}
=
−
10
cot
5
x
csc
2
5
x
{\displaystyle =-10\cot 5x\csc ^{2}5x}
11.
F
(
θ
)
=
tan
θ
−
θ
{\displaystyle F(\theta )=\tan \theta -\theta }
F
′
(
θ
)
{\displaystyle F'(\theta )}
=
tan
2
θ
{\displaystyle =\tan ^{2}\theta }
12.
f
(
ϕ
)
=
ϕ
sin
ϕ
+
cos
ϕ
{\displaystyle f(\phi )=\phi \sin \phi +\cos \phi }
f
′
(
ϕ
)
{\displaystyle f'(\phi )}
=
ϕ
cos
ϕ
{\displaystyle =\phi \cos \phi }
13.
f
(
t
)
=
sin
3
t
cos
t
{\displaystyle f(t)=\sin ^{3}t\cos t}
f
′
(
t
)
{\displaystyle f'(t)}
=
sin
2
t
(
3
cos
t
−
sin
2
t
)
{\displaystyle =\sin ^{2}t(3\cos ^{t}-\sin ^{2}t)}
14.
r
=
a
cos
2
θ
{\displaystyle r=a\cos 2\theta }
d
r
d
θ
{\displaystyle {\frac {dr}{d\theta }}}
=
−
2
a
sin
2
θ
{\displaystyle =-2a\sin 2\theta }
15.
d
d
x
sin
2
x
=
sin
2
x
{\displaystyle {\frac {d}{dx}}\sin ^{2}x=\sin 2x}
16.
d
d
x
cos
3
x
2
=
−
6
x
cos
2
x
2
sin
x
2
{\displaystyle {\frac {d}{dx}}\cos ^{3}x^{2}=-6x\cos ^{2}x^{2}\sin x^{2}}
17.
d
d
t
csc
t
2
2
=
−
t
csc
t
2
2
cot
t
2
2
{\displaystyle {\frac {d}{dt}}\csc {\frac {t^{2}}{2}}=-t\csc {\frac {t^{2}}{2}}\cot {\frac {t^{2}}{2}}}
18.
d
d
s
a
cos
2
s
=
−
a
sin
2
s
cos
2
s
{\displaystyle {\frac {d}{ds}}a{\sqrt {\cos 2s}}=-{\frac {a\sin 2s}{\sqrt {\cos 2s}}}}
19.
d
d
θ
a
(
1
−
cos
θ
)
=
a
s
i
n
θ
{\displaystyle {\frac {d}{d\theta }}a(1-\cos \theta )=asin\theta }
20.
d
d
x
(
log
cos
x
)
=
−
tan
x
{\displaystyle {\frac {d}{dx}}(\log \cos x)=-\tan x}
21.
d
d
x
(
log
tan
x
)
=
2
sin
2
x
{\displaystyle {\frac {d}{dx}}(\log \tan x)={\frac {2}{\sin 2x}}}
22.
d
d
x
(
log
sin
2
x
)
=
2
cot
x
{\displaystyle {\frac {d}{dx}}(\log \sin ^{2}x)=2\cot x}
23.
d
d
t
cos
a
t
=
a
t
2
sin
a
t
{\displaystyle {\frac {d}{dt}}\cos {\frac {a}{t}}={\frac {a}{t^{2}}}\sin {\frac {a}{t}}}
24.
d
d
θ
sin
1
θ
2
=
−
2
θ
3
cos
1
θ
2
{\displaystyle {\frac {d}{d\theta }}\sin {\frac {1}{\theta ^{2}}}=-{\frac {2}{\theta ^{3}}}\cos {\frac {1}{\theta ^{2}}}}
25.
d
d
x
e
sin
x
=
e
sin
x
cos
x
{\displaystyle {\frac {d}{dx}}e^{\sin x}=e^{\sin x}\cos x}
26.
d
d
x
sin
(
log
x
)
=
cos
(
log
x
)
x
{\displaystyle {\frac {d}{dx}}\sin(\log x)={\frac {\cos(\log x)}{x}}}
27.
d
d
x
tan
(
log
x
)
=
sec
2
(
log
x
)
x
{\displaystyle {\frac {d}{dx}}\tan(\log x)={\frac {\sec ^{2}(\log x)}{x}}}
28.
d
d
x
a
sin
3
θ
3
=
a
sin
2
θ
3
cos
θ
3
{\displaystyle {\frac {d}{dx}}a\sin ^{3}{\frac {\theta }{3}}=a\sin ^{2}{\frac {\theta }{3}}\cos {\frac {\theta }{3}}}
29.
d
d
α
sin
(
cos
α
)
=
−
sin
α
cos
(
cos
α
)
{\displaystyle {\frac {d}{d\alpha }}\sin(\cos \alpha )=-\sin \alpha \cos(\cos \alpha )}
30.
d
d
x
tan
x
−
1
sec
x
=
sin
x
+
cos
x
{\displaystyle {\frac {d}{dx}}{\frac {\tan x-1}{\sec x}}=\sin x+\cos x}
31.
y
=
log
1
+
sin
x
1
−
sin
x
{\displaystyle y=\log {\sqrt {\frac {1+\sin x}{1-\sin x}}}}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
cos
x
{\displaystyle ={\frac {1}{\cos x}}}
32.
y
=
log
tan
(
π
4
+
x
2
)
{\displaystyle y=\log \tan \left({\frac {\pi }{4}}+{\frac {x}{2}}\right)}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
cos
x
{\displaystyle ={\frac {1}{\cos x}}}
33.
f
(
x
)
=
sin
(
x
+
a
)
cos
(
x
−
a
)
{\displaystyle f(x)=\sin(x+a)\cos(x-a)}
f
′
(
x
)
{\displaystyle f'(x)}
=
cos
2
x
{\displaystyle =\cos 2x}
34.
y
=
a
tan
n
x
{\displaystyle y=a^{\tan nx}}
y
′
{\displaystyle y'}
=
n
a
tan
n
x
sec
2
n
x
log
a
{\displaystyle =na^{\tan nx}\sec ^{2}nx\log a}
35.
y
=
e
cos
x
sin
x
{\displaystyle y=e^{\cos x}\sin x}
y
′
{\displaystyle \ y'}
=
e
cos
x
(
cos
x
−
sin
2
x
)
{\displaystyle =e^{\cos x}(\cos x-\sin ^{2}x)\ }
36.
y
=
e
x
log
sin
x
{\displaystyle y=e^{x}\log \sin x}
y
′
{\displaystyle y'}
=
e
x
(
cot
x
+
log
sin
x
)
{\displaystyle =e^{x}(\cot x+\log \sin x)}
37. Differentiate the following functions:
(a)
d
d
x
sin
5
x
2
{\displaystyle {\frac {d}{dx}}\sin 5x^{2}}
(f)
d
d
x
csc
(
log
x
)
{\displaystyle {\frac {d}{dx}}\csc(\log x)}
(k)
d
d
t
e
a
−
b
cos
t
{\displaystyle {\frac {d}{dt}}e^{a-b\cos t}}
(b)
d
d
x
cos
(
a
−
b
x
)
{\displaystyle {\frac {d}{dx}}\cos(a-bx)}
(g)
d
d
x
sin
3
2
x
{\displaystyle {\frac {d}{dx}}\sin ^{3}2x}
(l)
d
d
t
sin
t
3
cos
2
t
3
{\displaystyle {\frac {d}{dt}}\sin {\frac {t}{3}}\cos ^{2}{\frac {t}{3}}}
(c)
d
d
x
tan
a
x
b
{\displaystyle {\frac {d}{dx}}\tan {\frac {ax}{b}}}
(h)
d
d
x
cos
2
(
log
x
)
{\displaystyle {\frac {d}{dx}}\cos ^{2}(\log x)}
(m)
d
d
θ
cot
b
θ
2
{\displaystyle {\frac {d}{d\theta }}\cot {\frac {b}{\theta ^{2}}}}
(d)
d
d
x
cot
a
x
{\displaystyle {\frac {d}{dx}}\cot {\sqrt {ax}}}
(i)
d
d
x
tan
2
1
−
x
2
{\displaystyle {\frac {d}{dx}}\tan ^{2}{\sqrt {1-x^{2}}}}
(n)
d
d
ϕ
1
+
cos
2
ϕ
{\displaystyle {\frac {d}{d\phi }}{\sqrt {1+\cos ^{2}\phi }}}
(e)
d
d
x
sec
e
3
x
{\displaystyle {\frac {d}{dx}}\sec e^{3x}}
(j)
d
d
x
log
(
sin
2
a
x
)
{\displaystyle {\frac {d}{dx}}\log(\sin ^{2}ax)}
(o)
d
d
s
log
1
−
2
sin
2
s
{\displaystyle {\frac {d}{ds}}\log {\sqrt {1-2\sin ^{2}s}}}
38.
d
d
x
(
x
n
e
sin
x
)
=
x
n
−
1
e
sin
x
(
n
+
x
cos
x
)
{\displaystyle {\frac {d}{dx}}(x^{n}e^{\sin x})=x^{n-1}e^{\sin x}(n+x\cos x)}
39.
d
d
x
(
e
a
x
cos
m
x
)
=
e
a
x
(
a
cos
m
x
−
m
sin
m
x
)
{\displaystyle {\frac {d}{dx}}(e^{ax}\cos mx)=e^{ax}(a\cos mx-m\sin mx)}
40.
f
(
θ
)
=
1
+
cos
θ
1
−
cos
θ
{\displaystyle f(\theta )={\frac {1+\cos \theta }{1-\cos \theta }}}
f
′
(
θ
)
{\displaystyle \ f'(\theta )}
=
−
2
sin
θ
(
1
−
cos
θ
)
2
{\displaystyle =\ -{\frac {2\sin \theta }{(1-\cos \theta )^{2}}}}
41.
f
(
ϕ
)
=
e
a
ϕ
(
a
sin
ϕ
−
cos
ϕ
)
a
2
+
1
{\displaystyle f(\phi )={\frac {e^{a\phi }(a\sin \phi -\cos \phi )}{a^{2}+1}}}
f
′
(
ϕ
)
{\displaystyle \ f'(\phi )}
=
e
a
ϕ
sin
ϕ
{\displaystyle =\ e^{a\phi }\sin \phi }
42.
f
(
s
)
=
(
s
cot
s
)
2
{\displaystyle \ f(s)=(s\cot s)^{2}}
f
′
(
s
)
{\displaystyle \ f'(s)}
=
2
s
cot
s
(
cot
s
−
s
csc
2
s
)
{\displaystyle =\ 2s\cot s(\cot s-s\csc ^{2}s)}
43.
r
=
1
3
tan
3
θ
−
tan
θ
+
θ
{\displaystyle r={\frac {1}{3}}\tan ^{3}\theta -\tan \theta +\theta }
d
r
d
θ
{\displaystyle {\frac {dr}{d\theta }}}
=
tan
4
θ
{\displaystyle =\tan ^{4}\theta }
44.
y
=
x
sin
x
{\displaystyle y=x^{\sin x}\ }
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
x
sin
x
(
sin
x
x
+
log
x
cos
x
)
{\displaystyle =\ x^{\sin x}\left({\frac {\sin x}{x}}+\log x\cos x\right)}
45.
y
=
(
sin
x
)
x
{\displaystyle y=(\sin x)^{x}\ }
y
′
{\displaystyle \ y'}
=
(
sin
x
)
x
[
log
sin
x
+
x
cot
x
]
{\displaystyle =\ (\sin x)^{x}[\log \sin x+x\cot x]}
46.
y
=
(
sin
x
)
tan
x
{\displaystyle y=(\sin x)^{\tan x}\ }
y
′
{\displaystyle \ y'}
=
(
sin
x
)
tan
x
(
1
+
sec
2
x
log
sin
x
)
{\displaystyle =\ (\sin x)^{\tan x}(1+\sec ^{2}x\log \sin x)}
47. Prove
d
d
x
cos
v
=
−
sin
v
d
v
d
x
{\displaystyle {\frac {d}{dx}}\cos v=-\sin v{\frac {dv}{dx}}}
General Rule .
48. Prove
d
d
x
cot
v
=
−
csc
2
v
d
v
d
x
{\displaystyle {\frac {d}{dx}}\cot v=-\csc ^{2}v{\frac {dv}{dx}}}
cot
v
{\displaystyle \cot v}
cos
c
sin
v
{\displaystyle {\frac {\cos c}{\sin v}}}
55. Differentiation of
arcsin
v
{\displaystyle \arcsin v}
Let
y
{\displaystyle \ y}
=
arcsin
v
{\displaystyle =\arcsin \ v}
[ 1]
then
v
{\displaystyle \ v}
=
sin
y
{\displaystyle =\sin \ y}
Differentiating with respect to
y
{\displaystyle y}
XI ,
d
v
d
y
{\displaystyle {\frac {dv}{dy}}}
=
cos
y
{\displaystyle =\cos \ y}
therefore
d
y
d
v
{\displaystyle {\frac {dy}{dv}}}
=
1
cos
y
{\displaystyle ={\frac {1}{\cos y}}}
By (C [§ 43]
But since
v
{\displaystyle v}
x
{\displaystyle x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
(A [§ 42]
giving
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
cos
y
⋅
d
v
d
x
{\displaystyle ={\frac {1}{\cos y}}\cdot {\frac {dv}{dx}}}
=
1
1
−
v
2
d
v
d
x
{\displaystyle ={\frac {1}{\sqrt {1-v^{2}}}}{\frac {dv}{dx}}}
[
cos
y
=
1
−
sin
2
y
=
1
−
v
2
{\displaystyle [\cos y={\sqrt {1-\sin ^{2}y}}={\sqrt {1-v^{2}}}}
cos
y
{\displaystyle \cos y}
y
{\displaystyle y}
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
XVIII
∴
d
d
x
(
arcsin
v
)
{\displaystyle {\frac {d}{dx}}(\arcsin v)}
=
d
v
d
x
1
−
v
2
{\displaystyle ={\frac {\frac {dv}{dx}}{\sqrt {1-v^{2}}}}}
56. Differentiation of
arccos
v
{\displaystyle \arccos v}
Let
y
{\displaystyle \ y}
=
arccos
v
{\displaystyle =\arccos \ v}
[ 2]
then
y
{\displaystyle \ y}
=
cos
y
{\displaystyle =\cos \ y}
Differentiating with respect to
y
{\displaystyle y}
XII ,
d
v
d
y
{\displaystyle {\frac {dv}{dy}}}
=
−
sin
y
{\displaystyle =-\sin \ y}
therefore
d
y
d
v
{\displaystyle {\frac {dy}{dv}}}
=
−
1
sin
y
{\displaystyle =-{\frac {1}{\sin y}}}
By (C [§ 43]
But since
v
{\displaystyle v}
x
{\displaystyle x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
(A [§ 42]
giving
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
−
1
sin
y
⋅
d
v
d
x
{\displaystyle =-{\frac {1}{\sin y}}\cdot {\frac {dv}{dx}}}
=
−
1
1
−
v
2
d
v
d
x
{\displaystyle =-{\frac {1}{\sqrt {1-v^{2}}}}{\frac {dv}{dx}}}
[
sin
y
=
1
−
cos
2
y
=
1
−
v
2
{\displaystyle \sin y={\sqrt {1-\cos ^{2}y}}={\sqrt {1-v^{2}}}}
sin
y
{\displaystyle \sin y}
XIX
∴
d
d
x
(
arccos
v
)
{\displaystyle {\frac {d}{dx}}(\arccos v)}
=
−
d
v
d
x
1
−
v
2
{\displaystyle =-{\frac {\frac {dv}{dx}}{\sqrt {1-v^{2}}}}}
57. Differentiation of
arctan
v
{\displaystyle \arctan v}
Let
y
{\displaystyle \ y}
=
arctan
v
{\displaystyle =\ \arctan v}
[ 3]
then
y
{\displaystyle \ y}
=
tan
y
{\displaystyle =\ \tan y}
Differentiating with respect to
y
{\displaystyle y}
XIV ,
d
v
d
y
{\displaystyle {\frac {dv}{dy}}}
=
sec
2
y
{\displaystyle =\ \sec ^{2}y}
therefore
d
y
d
v
{\displaystyle {\frac {dy}{dv}}}
=
1
sec
2
y
{\displaystyle ={\frac {1}{\sec ^{2}y}}}
By (C [§ 43]
But since
v
{\displaystyle v}
x
{\displaystyle x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
(A [§ 42]
giving
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
sec
2
y
⋅
d
v
d
x
{\displaystyle ={\frac {1}{\sec ^{2}y}}\cdot {\frac {dv}{dx}}}
=
1
1
+
v
2
d
v
d
x
{\displaystyle ={\frac {1}{1+v^{2}}}{\frac {dv}{dx}}}
[
sec
2
y
=
1
+
tan
2
y
=
1
+
v
2
{\displaystyle \sec ^{2}y=1+\tan ^{2}y=1+v^{2}}
XX
∴
d
d
x
(
arctan
v
)
{\displaystyle {\frac {d}{dx}}(\arctan v)}
=
d
v
d
x
1
+
v
2
{\displaystyle ={\frac {\frac {dv}{dx}}{1+v^{2}}}}
58. Differentiation of
arccot
u
{\displaystyle \operatorname {arccot} u}
[ 4]
Following the method of the last section, we get
XXI
d
d
x
(
arccot
v
)
=
−
d
v
d
x
1
+
v
2
{\displaystyle {\frac {d}{dx}}(\operatorname {arccot} v)=-{\frac {\frac {dv}{dx}}{1+v^{2}}}}
59. Differentiation of
arcsec
u
{\displaystyle \operatorname {arcsec} u}
Let
y
{\displaystyle \ y}
=
arcsec
v
{\displaystyle =\ \operatorname {arcsec} v}
[ 5]
then
v
{\displaystyle \ v}
=
sec
y
{\displaystyle =\ \sec y}
Differentiating with respect to
y
{\displaystyle y}
IV ,
d
v
d
y
{\displaystyle {\frac {dv}{dy}}}
=
sec
y
tan
y
{\displaystyle =\ \sec y\tan y}
therefore
d
y
d
v
{\displaystyle {\frac {dy}{dv}}}
=
1
sec
y
tan
y
{\displaystyle ={\frac {1}{\sec y\tan y}}}
By (C [§ 43]
But since
v
{\displaystyle v}
x
{\displaystyle x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
(A [§ 42]
giving
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
sec
y
tan
y
d
v
d
x
{\displaystyle ={\frac {1}{\sec y\tan y}}{\frac {dv}{dx}}}
=
1
v
v
2
−
1
d
v
d
x
{\displaystyle ={\frac {1}{v{\sqrt {v^{2}-1}}}}{\frac {dv}{dx}}}
[
sec
y
=
v
{\displaystyle \sec y=v}
tan
y
=
sec
y
−
1
=
v
2
−
1
{\displaystyle \tan y={\sqrt {\sec y-1}}={\sqrt {v^{2}-1}}}
tan
y
{\displaystyle \tan y}
y
{\displaystyle y}
π
2
{\displaystyle {\frac {\pi }{2}}}
−
π
{\displaystyle -\pi }
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
−
π
{\displaystyle -\pi }
XXII
∴
d
d
x
(
arcsec
v
)
{\displaystyle {\frac {d}{dx}}(\operatorname {arcsec} v)}
=
d
v
d
x
v
v
2
−
1
{\displaystyle ={\frac {\frac {dv}{dx}}{v{\sqrt {v^{2}-1}}}}}
60. Differentiation of
arccsc
v
{\displaystyle \operatorname {arccsc} v}
[ 6]
Let
y
{\displaystyle \ y}
=
arccsc
v
{\displaystyle =\ \operatorname {arccsc} v}
then
v
{\displaystyle \ v}
=
csc
y
{\displaystyle =\ \csc y}
Differentiating with respect to
y
{\displaystyle y}
XVI and following the method of the last section, we get
XXIII
d
d
x
(
arccsc
v
)
{\displaystyle {\frac {d}{dx}}(\operatorname {arccsc} v)}
=
−
d
v
d
x
v
v
2
−
1
{\displaystyle =-{\frac {\frac {dv}{dx}}{v{\sqrt {v^{2}-1}}}}}
61. Differentiation of
arcvers
v
{\displaystyle \operatorname {arcvers} v}
Let
y
{\displaystyle \ y}
=
arcvers
v
{\displaystyle =\operatorname {arcvers} v}
[ 7]
then
v
{\displaystyle \ v}
=
vers
y
{\displaystyle =\operatorname {vers} y}
Differentiating with respect to
y
{\displaystyle y}
XVII ,
d
v
d
y
{\displaystyle {\frac {dv}{dy}}}
=
sin
y
{\displaystyle =\ \sin y}
therefore
d
y
d
v
{\displaystyle {\frac {dy}{dv}}}
=
1
sin
y
{\displaystyle ={\frac {1}{\sin y}}}
By (C [§ 43]
But since
v
{\displaystyle v}
x
{\displaystyle x}
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
d
y
d
v
⋅
d
v
d
x
{\displaystyle ={\frac {dy}{dv}}\cdot {\frac {dv}{dx}}}
(A [§ 42]
giving
d
y
d
x
{\displaystyle {\frac {dy}{dx}}}
=
1
sin
y
⋅
d
v
d
x
{\displaystyle ={\frac {1}{\sin y}}\cdot {\frac {dv}{dx}}}
=
1
2
v
−
v
2
d
v
d
x
{\displaystyle ={\frac {1}{\sqrt {2v-v^{2}}}}{\frac {dv}{dx}}}
[
sin
y
=
1
−
cos
2
y
=
1
−
(
1
−
vers
y
)
2
=
2
v
−
v
2
{\displaystyle \sin y={\sqrt {1-\cos ^{2}y}}={\sqrt {1-(1-\operatorname {vers} y)^{2}}}={\sqrt {2v-v^{2}}}}
sin
y
{\displaystyle \sin y}
y
{\displaystyle y}
π
{\displaystyle \pi }
XXIV
∴
d
d
x
(
arcvers
v
)
{\displaystyle {\frac {d}{dx}}(\operatorname {arcvers} v)}
=
d
v
d
x
2
v
−
v
2
{\displaystyle ={\frac {\frac {dv}{dx}}{\sqrt {2v-v^{2}}}}}
↑ Graph of arc sin v
v
{\displaystyle v}
y
{\displaystyle y}
v
{\displaystyle v}
y
=
arcsin
v
{\displaystyle y=\arcsin v}
v
=
O
M
,
y
=
M
P
1
,
M
P
2
,
M
P
3
,
⋯
,
M
Q
1
M
Q
2
,
⋯
{\displaystyle v=OM,y=MP_{1},MP_{2},MP_{3},\cdots ,MQ_{1}MQ_{2},\cdots }
y
{\displaystyle y}
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
Q
O
P
{\displaystyle QOP}
v
{\displaystyle v}
↑ Graph of arc cos v
v
{\displaystyle v}
y
=
arccos
v
{\displaystyle y=\arccos v}
v
=
O
M
,
y
=
M
P
1
,
M
P
2
,
⋯
,
M
Q
1
M
Q
2
,
⋯
{\displaystyle v=OM,y=MP_{1},MP_{2},\cdots ,MQ_{1}MQ_{2},\cdots }
y
{\displaystyle y}
y
{\displaystyle y}
v
{\displaystyle v}
↑ Graph of arc tan v
v
{\displaystyle v}
y
{\displaystyle y}
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
v
{\displaystyle v}
A
O
E
{\displaystyle AOE}
↑ Fig. a. Graph of arc cot v
v
{\displaystyle v}
a ). In order to make it single-valued, only values of
y
{\displaystyle y}
π
{\displaystyle \pi }
v
{\displaystyle v}
AB .
↑ Fig b. Graph of arc sec v
v
{\displaystyle v}
y
{\displaystyle y}
v
{\displaystyle v}
v
{\displaystyle v}
AB (Fig. b),
y
{\displaystyle y}
π
2
{\displaystyle {\frac {\pi }{2}}}
v
{\displaystyle v}
DC ,
y
{\displaystyle y}
−
π
{\displaystyle -\pi }
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
−
π
{\displaystyle -\pi }
↑ Graph of y = arc csc v
v
{\displaystyle v}
y
{\displaystyle y}
v
{\displaystyle v}
v
{\displaystyle v}
AB (Fig. a),
y
{\displaystyle y}
π
2
{\displaystyle {\frac {\pi }{2}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
v
{\displaystyle v}
CD ,
y
{\displaystyle y}
−
π
{\displaystyle -\pi }
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
−
π
2
{\displaystyle -{\frac {\pi }{2}}}
↑
v
{\displaystyle v}
y
{\displaystyle y}
v
{\displaystyle v}
y
{\displaystyle y}
π
{\displaystyle \pi }
O
P
{\displaystyle OP}
a ).
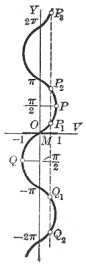
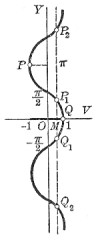




 Defined only for values of between 0 and 2 inclusive, and is many-valued. To make the function continuous, is taken as the smallest positive arc whose versed sine is ; that is, lies between 0 and inclusive. Hence we confine ourselves to arc of the graph (Fig. a).
Defined only for values of between 0 and 2 inclusive, and is many-valued. To make the function continuous, is taken as the smallest positive arc whose versed sine is ; that is, lies between 0 and inclusive. Hence we confine ourselves to arc of the graph (Fig. a).









































































































































![{\displaystyle =\ (\sin x)^{x}[\log \sin x+x\cot x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c9beb166fa9bc9b0d811be2333d463106dbeb3a)
























































































