Great Neapolitan Earthquake of 1857/Part I. Ch. IV

by Robert Mallet

CHAPTER IV.

FIRST CLASS OF DETERMINANTS—FRACTURES IN RECTANGULAR
BUILDINGS AS EVIDENCES OF WAVE-PATH.

---

If an isolated wall (a parallelopiped) of masonry or brick, founded on level ground, be subjected to the transit of an earth wave, whose velocity is sufficient to affect the continuity of its parts, the resulting fractures will vary with the direction of the wave-path as respects the plane of the wall, and with the angle of emergence of the wave.

1st. If the wave-path be horizontal, or nearly so, and in the plan of the wall, the earth moving forward beneath the wall, tends to carry it forward by the grasp of its foundation and at its own velocity; but this is opposed by the wall's inertia. The material of the wall being, within narrow limits flexible and elastic, the tendency is to distort its figure, thus.

The wave reaching the end $a$ (Fig. 14 bis) first, with a transit from $a$ towards $b$, the end $a$ first begins to assume the form $ea$, rapidly taken by the whole wall, if sufficiently high in relation to its length. The wave traverses beneath the whole length, the materials, in virtue of their elasticity, oscillate in the same direction between $e$ and $f$ throughout the whole mass, and if the wall be fissured, it will be by a nearly vertical crack, widest open at top, and extending more or less down towards the base. If the wall were of absolutely uniform cohesion, there would be two such fissures near either end, or only one in the mid length, dependent upon the density, cohesion, and rate of force transmission of its materials, and the velocity of the wave movement: practically, such a wall is usually fissured in the weakest place.

2nd. If the wave transit be horizontal, or nearly so, and oblique to the plane of the wall, the latter either falls prostrate wholly, or a triangular fragment is thrown off from the end last reached by the wave, and in the direction contrary to its transit, or the wall is fissured, as in the first case only, dependent chiefly upon the greater or less obliquity of the line of transit to the plane of the wall.

Isolated walls, exposed to oblique or to directly transverse action, thus when tolerably thick, may sometimes be twisted considerably out of plumb without losing equilibrium or complete cohesion.

3rd. If the wave emerge with a steep angle to the horizon, the distortion is that of compression in the diagonal of the wall's plane, nearest parallel to the line of wave transit; and the fissures, if they occur, are also diagonal to the horizon, and approximate to directions perpendicular to the lines of pressure, i.e., to the line of wave transit. If the velocity of the wave be sufficient, in relation to the density and cohesion of the wall, a triangular mass may be projected from the end at which the wave passes out from it.

Reference will frequently occur to the directions in azimuth and emergence of the earth wave, relative to those of walls, buildings, or other objects affected by it. It will be convenient, therefore, to fix a nomenclature for these relations. A rectangular building, two of whose walls run north and south, and the other two east and west, may be called a cardinal building: buildings whose four walls run in any other azimuths will be described as ordinal.

Referring generally to the direction of wave transit in its horizontal component, or when nearly horizontal, as affecting cardinal buildings (which alone are generally suited for observation), it will be denominated normal when its azimuth is parallel to either pair of walls, viz., either north and south, or east and west.

When the line of wave transit, or its horizontal component, are in some intermediate azimuth, it will be said to be abnormal.

When a normal wave is an emergent one (the line of transit, or wave-path, inclined to the horizon) it will be called a subnormal wave; and in a similar case the abnormal wave will be designated as subabnormal.

These expressions will save much prolixity.

When the observer first enters upon one of those earthquake-shaken towns, he finds himself in the midst of utter confusion. The eye is bewildered by "a city become an heap." He wanders over masses of dislocated stone and mortar, with timbers half buried, prostrate, or standing stark up against the light, and is appalled by spectacles of desolation (such as those in Photogs. Nos. 15, 16, 17, 18, 19, and 20, Coll. Roy. Soc.).

At first sight, and even after cursory examination, all appears confusion. Houses seem to have been precipitated to the ground in every direction of azimuth. There seems no governing law, nor any indication of a prevailing direction of overturning force. It is only by first gaining some commanding point, whence a general view over the whole field of ruin can be had, and observing its places of greatest and least destruction, and then by patient examination, compass in hand, of many details of overthrow, house by house and street by street, analyzing each detail and comparing the results, as to the direction of force, that must have produced each particular fall, with those previously observed and compared, that we at length perceive, once for all, that this apparent confusion is but superficial.

We discover the cause, and in doing so obtain the key to all future correct and ready detection of the general directions of shock, by having learned to choose the proper class of buildings for our observations.

We find that wherever the ruin is complete and featureless—defying deduction—there the streets have been narrowed to five or twelve feet wide, have run winding hither and thither, ascending and descending, and that the walls of the houses, following their irregularities, have stood in every possible azimuth; that the exposed fronts and sides of the houses have faced every point of the compass; and often that the confusion produced by the shock thus reaching walls at the same moment at every conceivable angle, has been further increased by the falling houses having staggered against each other, and so some that might if alone have fallen in other ways, or might have escaped with only fissures, have been beaten to the earth by their neighbours. This sort of destruction, too, we will have remarked, belongs to the poorest habitations and worst built and densest parts of the town, where the wretched rubble masonry falls incoherent at the slightest jar.

We advance then to the churches, the barracks, or castello, the monasteries, the Casa Communale—to any of the better built and isolated, or nearly isolated buildings, and we soon discover that amongst these there are some that in every place present certain grand characteristics of partial or complete overthrow, and that these are everywhere generically much alike.

These we observe, aided by the prismatic compass, and with our previous dynamic knowledge, and soon discover that wherever such buildings, and not very dissimilar to each other, have been placed under like conditions, and so that their walls are in the same azimuths, like dislocations have affected them, and that where the directions in which the forces that we know must have produced the observed dislocations have not passed very diagonally through the walls, they have produced effects, regular and accordant with each other, and from which the directions may be inferred in which the forces themselves acted.

After a little experience we discover, that in every town (and frequently in other places) we may find rectangular buildings whose walls run very nearly north and south and east and west, and that these respond to our questions best; and finally, that buildings so posited, and having certain necessary characters of structure, when not too completely destroyed or overthrown, will enable us to discover the direction of wave transit, whatever may have been its line with reference to the walls.

It remains to describe, therefore, the effects produced upon such cardinal buildings by earthquake shock, to trace from the effects their causes—from the dislocations the forces that produced them and their directions, and to point out some of the more important modifications of effect due to differences of masonry, of form, of architecture, of wall apertures, and other such accidental conditions.

Commencing with the simplest case. If a cardinal building consisting merely of four unroofed walls be exposed to a normal shock, capable of fissuring the masonry, but not completely overthrowing it, the fissures will be found as nearly vertical cracks following the joints of the masonry, and within a few feet (more or less) of each quoin, as in Fig. 21-23, and Fig. 22-24, in plan.

The fissures being widest at top, and becoming a scarce visible line at part of the way down the walls, or perhaps extending to their base, the earth wave, if in the direction $a$ to $b$, reaches the end wall, $a$, first. Its inertia acts as an equal and opposite force at its centre of gravity, and tends to cause it to be left behind while the remainder of the building is pushed forward. The end wall towards the direction from which the shock has come moves in the opposite one, and if fracture occur the side walls fissure a short way off from the quoins, and the movement of the end wall is one of rotation round some horizontal line or lines situated along the length of its base.

Were every part of the walls of the building of perfectly equal coherence, and the rate of wave transit the same in its materials as that of the earth wave, the fracture would occur exactly at the internal angle of the wall at each quoin, breaking the side walls across in a plane coinciding with that of the internal face of the end wall. But the quoins are in practice built with larger, longer bedded, and better dressed masonry than the rest of the structure; and hence from this cause alone, without reference to others, the fissures are removed along the side walls nearer the middle, and into the less coherent masonry of the walls, and take place at $c$.

The earth wave pushes the side walls along with it, and these push the end wall $b$ at either quoin before them. The end wall $b$ therefore cannot fall by inertia in the same way as that, $a$, being propped up by the side walls. The earth wave, however, having passed its first semiphase, returns through the second half vibration in the opposite direction, and, we may assume, with equal velocity. The same set of forces now operate upon the end wall, $b$, the movement of the whole mass being in the direction $b$ to $a$, and as described for the former end wall; so that $b$ tends to turn over upon its base in the contrary direction to the movement of the wave itself in its second semiphase, and the side walls are fissured as before at a distance from the quoins greater or less along them, as at $e$ (Fig. 21). As the force producing fracture and dislocation at any given velocity is always proportionate to $\mathrm {M}$—the mass broken off or dislodged—so the extent of dislodgement after fracture (the materials being the same) is always proportionate to the velocity; and hence in any one building of like material and masonry the width of each fissure is proportionate to the velocity that has been effective in opening it; and we may compare component velocities in the directions of the planes of parallel or abutting walls by means of the widths of such fissures, the width in every case being measured with reference to an unit in length of the fissure from its origin, or where it becomes evanescent. This unit length may be arbitrary, but 10 feet in length of fissure is a very convenient unit, and the widths expressed in inches and decimals for that unit.

It is almost invariably found that in every building (with certain exceptions, to be noticed), although the masonry and form, &c., of the building may be quite or very nearly alike at both ends, the fissures $c$ and $e$, do not occur at equal distances from the respective quoins (measured along the side walls), nor are they equally opened, large, and long, at both the opposite ends.

Whether this arises—as, from other considerations respecting the vibration of pendulous lamps set in motion by shock, and to be hereafter noticed (Part III.), seems probable—from a real difference in velocity in the two semiphases of the wave itself, and that the second semiphase is described with a somewhat slower velocity than the first, owing to defect of perfect elasticity in material substances composing the earth's surface—or whether it is due to the conjoint action of the elastic wave (the earth wave) itself, and of the wave of elastic compression of the materials of the walls themselves—or to whatever other cause, which future research must make clear, the fact may be accepted as certain and very general—that the end wall which is first acted upon by the wave (whenever it is something near normal), has the higher velocity shown upon it, and that the fissures at that end are, cœteris paribus, found to be wider than those at the opposite one.

The fissure formed at the end $a$, that first reached, is frequently rather wider than what is precisely due to this difference in velocity in the two semiphases of the wave; for the end $a$ is first fissured, the end $b$ is next fissured by the second semiphase, which leaves the end wall $b$ broken off, behind it, but carries back with it both side walls in the direction of its own return motion, and towards the end wall $a$. But more or less dust and broken fragments are often intercepted in the fissure $a$ when first opened. These hinder the mass broken off at $a$ from approaching the side walls, and closing the fissures (by the inertia of the broken-off mass), so that the side walls, in this return movement, push the end wall $a$ before them, through the intervention of these obstacles, and so a second movement is impressed (small in extent) upon the broken-off end $a$, in the contrary direction to the wave transit, and in the same direction with its first movement, which ends by increasing the final width of the fissures at the end $a$.

The chief disturbing causes that interfere with and mask the regularity of this phenomenon are—The wave being subnormal and emergent at a considerable angle; in which case the length of the dynamic couple (as has been already generally explained) that measures the overthrowing and dislocating power at a given velocity, is greatest in the second semiphase of the wave, and to such an extent, as to obliterate the effect of the difference in velocity of the two semiphases, and either leave the fissures equal at both ends, or even make those at the end $b$ the wider.

Inequalities in the materials or masonry at the opposite ends in the line of the wave-path—want of complete or nearly approximate symmetry in the size and form of those ends—perforations of doors or windows, or such-like sudden changes of continnity of wall—and great length of bond in the wall stones at all or at a few points—are the other conditions which chiefly perplex and interfere with the phenomenon.

Practically, however, this fact is a guide of much importance in seismic observation, inasmuch as it enables us very frequently to decide, with more or less certainty, as to the direction of wave transit, from conditions that otherwise would afford no information beyond that of the path of the wave, leaving it quite uncertain whether the seismic vertical were to be sought for towards $a$ or towards $b$.

Where the phenomena are clear, we may, on the contrary, always conclude that it lies along the wave-path, towards the end that presents the widest fissures. Very few large and massive cardinal buildings will be found that will not give, as respects a normal or slightly subnormal wave, a decisive response, from some or other of its parts, by this means.

The actual phenomena in a well-developed case are illustrated in the Photog. No. 25, which shows th front end of the church of Pertosa, looking at its N.W. end. The direction of the nearly horizontal wave that

CHURCH at PERTOSA, Looking North West.		CATHEDRAL OF MARSICO NUOVO. North Side.

produced these fissures having been almost parallel to the west end wall, and from the N.E. to the S.W., or from left to right of the picture. The wave of shock was of very steep emergence at Pertosa; but the whole "colline" upon which the town is perched, oscillated laterally with the wave, and horizontally, or nearly so. The horizontal fractures, and those over the door, are due to the emergent wave only.

The force producing fracture and dislocation, impressed by the shock, may be viewed as separated into two-one just sufficient to fracture the materials, the other to dislodge them more or less. Both depend upon the velocity at maximum of the wave; but the power to produce fracture depends much more upon velocity than upon the amplitude of the wave, while the energy to produce dislocation after fracture depends also upon the latter, which determines the time during which the motion of the passing wave acts upon the mass.

The flexibility and elasticity of masonry or brickwork, even of the highest quality, in masses of ordinary size is small, the limits of distortion without rupture narrow: the compressive or extending forces being due to inertia, are proportional to $\mathrm {MV}$, and for the same material proportionate to $\mathrm {V}$ only; and as the amount of extension or compression, for the unit of length due to any force suddenly applied to an elastic solid, is double that produced by the same force, if statically or slowly applied, the effect of a high velocity is to produce fracture with great facility in bodies of narrow elastic limits. A wave shock of extremely small amplitude, therefore—one so small as not to appeal at all alarmingly to our senses—may yet be competent to produce considerable fractures in buildings; but in this case the fissures will be found to be close and thread-like.

Were the mass of a wall (viewed as a single parallelopiped) so circumstanced that, its integrant portions, retaining their relative positions merely, were free to oscillate, and then to remain at the points which they occupied at the moment the wave left them, having no resilience, in such case the chord of the arc of movement at the centre of oscillation would be very nearly equal to the amplitude of the wave that produced the oscillation; and this would be equally true of the width of a fissure produced in such a wall. Now, we occasionally find walls that are extremely massive in proportion to their altitude, and built of small stones or brick laid in bad masonry, and with almost bondless mortar; such walls have little or no resilience, and, when thrown more or less out of plumb, or fissured, with suitable conditions, afford a rude approximate measure of the horizontal amplitude of the earth wave, by the range of movement impressed at the level of the centre of oscillation. Some examples of this, as observed, will be found in Part II.

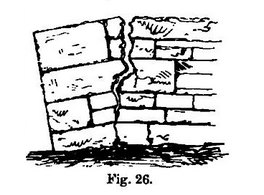
The adhesion of mortars and cements to stone or brick, in a direction perpendicular to the faces of the joints of the work, is always much less, with the ordinary materials employed, than the cohesion of the latter for equal sections; the exceptions being only buildings of very soft tufa, or some such stuff. Hence, although fracture and open fissures may occur occasionally, running right through some stones and breaking them across in a building which may be acted on transversely, as when very long upon their beds, and crossing a line of fissure near the axis of revolution, thus (Fig. 26); it nevertheless almost invariably happens that the line of fracture, whether in stonework or brickwork, follows down or along a line of joints, producing a jagged or serrated fissure, the jaws or serrations depending upon the length of bed of each block or brick, and the depth of the courses.

It has been found that the adhesion of Portland cement to Portland stone is only 146 lbs. per square inch, while the cohesion of the cement itself is 400 lbs. per square inch, or the former little more than one-third; and that the adhesion of Parker's cement to granite is as low as 22 lbs. per square inch, the cohesion of the cement being 300 lbs. per square inch, or less than one-thirteenth. The adhesion of common lime mortar varies enormously, with the nature of its materials, the sort of stone or brick which it is used to cement, the thickness of the joints, the care taken to fill them effectually and solidly, the degree of wetness or dryness of the mortar itself and of the stone or brick to which it has been applied, and the rate at which the mortar has been dried during its setting, and the amount of moisture and of air to which it has been subsequently exposed. All these conditions, or some of them, have been found sufficient to make a difference of absolute cohesion of more than 2 : 1 between old Roman mortar consolidated and hardened for ages, and good modern mortar allowed sufficient time to be viewed as fully set or indurated. When very dry, mortar. is much more brittle and easily fractured than when wet even after complete induration Such conditions, and others similar, but tedious to detail, must be known to, and constantly looked out for, by the seismic observer in the field, or otherwise he will continually be liable to compare, as to effects, unlike and incomparable buildings or circumstances.

The coefficients of cohesion which apply to our equations of fracture will be given hereafter.

Returning now to Figs. 23 and 24. If the path of the wave be normal as before, but its velocity and amplitude greater than are sufficient only to cause fissures, then one or both end walls may be overthrown. If the direction of the transit be from $a$ to $b$, the end wall $a$ will be prostrated outwards, or in the contrary sense. The end wall $b$, propped, as before explained, by the side walls, may possibly be projected outwards and fall also; but in most instances there will be only fissures produced at its end, as in Figs. 21, 22.

This may be made clearer by referring to Fig. 27. Let $\mathrm {AE}$ be the path of the wave, its direction of transit being

from $\mathrm {A}$ towards $\mathrm {E}$, and the form of the wave vibration cut by a vertical plane, be $\mathrm {A} p\mathrm {C} q$ at the end $a$, and the same when it has progressed to that $b$; bearing in mind, however, that the amplitude of the wave, as it actually occurs in earthquake, is very great in proportion to its altitude, in most cases, indeed in every case of a normal or nearly normal wave, and that during its transit the whole building is simultaneously in motion.

The end wall begins to be affected by its own inertia at the moment that the forward phase of the wave $\mathrm {A}$ to $\mathrm {C}$ reaches it. The velocity of the vibrating mass increases to the maximum at the point $p$; when whatever fissure may take place occurs, and the centre of gravity of the mass begins to move in the direction from $\mathrm {C}$ to $\mathrm {A}$, the whole turning round the point $x$ at the base. This movement is continued, though with diminished energy, by the wave motion during the second half of its first semi-vibration, i.e., from $p$ to $\mathrm {C}$, when it passes through zero, and now, during the whole of the second semi-vibration from $\mathrm {C}$ to $\mathrm {A}$, passing through the second maximum at $q$, the motion of the earth is in a contrary sense to that of the wall, and of the wave transit.

It has set the detached mass in motion with a momentum = $\mathrm {MV}$, $\mathrm {V}$ being the velocity of first semiphase of the wave itself at its maximum. It tends to destroy this during the second half vibration, by a momentum = $\mathrm {M} (\mathrm {V} -v)$, $v$ being the difference of velocity in the semiphases. During the time of the second half, of the first semi-vibration from $p$ (when fracture occurs) to $\mathrm {A}$, the wall continues to fall or turn over outwards, and for a little beyond this; but this is now checked by the return or second semi-vibration, and unless the angular motion of the mass in the time from $p$ to $\mathrm {A}$ shall have carried its centre of gravity beyond the vertical passing through $x$, the wall shall not fall. If such be the case—i.e., if the wall do not fall—a contrary motion, more or less tending to restore its position, is impressed upon it in the return from $\mathrm {C}$ through $q$ to $\mathrm {A}$, and it comes to rest, with the fissure somewhat closer than it was, at an intermediate moment just after its formation, unless fragments have fallen between and prevented this, and always assuming that its parts hold coherent. Proceeding now to follow the train of action upon the end wall $b$, the wave affecting almost simultaneously the whole building, the two side walls and the end wall $b$ are forced forward together, the movement as before, commencing at the instant the initial movement of the wave $\mathrm {D}$ reaches them. They both (side and end walls) pass through the point $r$ of maximum velocity nearly together, and so to $\mathrm {E}$, when the motion of the wave itself is zero, and the motion of its second semi-vibration commences, which is retrograde as before.

Fracture cannot occur at the end $b$ during the first semi-vibration $\mathrm {D} r\mathrm {E}$, because the side and end walls are alike urged forward together and at equal velocities: there is therefore nothing to produce separation. If fracture, therefore, take place at the end $b$, it must occur at the point of maximum velocity $s$, in the second semi-vibration, from which to $\mathrm {D}$, the motion of the wave continues to promote separation; but the momentum impressed at $s$ is = $\mathrm {M} (\mathrm {V} -v)$, whereas at the former end at $p$ it was $\mathrm {MV}$. The force necessary to produce fracture of the materials being the same at both ends (which is, however, only strictly true for absolutely equal velocities), the amount of movement impressed upon the mass at the end $a$, will be greater than that at the end $b$, by the momentum due to $\mathrm {M} v$, (neglecting any small restoration of position of $a$, at the return semiphase of the wave), and so if fissures only be produced, those at $a$ will be wider than those at $b$, as was before stated; or if the impressed movement be capable of more than this, the end wall $a$ will be prostrated; and that $b$ may stand, but fissured from the side walls, or with still greater violence, it, too, may be thrown forwards in the same direction as that of the wave transit, but to a less horizontal distance.

Were the building in Figs. 21-23 square in plane, instead of rectangular, it will readily be conceived that precisely the same phenomena must succeed to a normal wave, whose path should be orthogonal to one in the direction $a...b$ or in $s...t$.

If, however, the building be rectangular, and with the sides $ce$ and $hk$ of considerable absolute length, and largely exceeding that of the ends, and the path of a normal wave be through them in the direction $a...b$ (Fig. 28), it then rarely happens that fissures occur, or occur alone near the quoins.

The wave, as before, passes from $a$ towards $b$, and the side wall $ce$, as before, moves by inertia in the contrary sense; and were it sufficiently rigid along its length, it might tear off from the ends, and fissures occur as before at $nn$, $n'n'$, the other side wall $hk$ following the movement already described for $b$ (Figs. 21-23).

The whole length of $ce$ has an equal velocity impressed; it is unsupported for its whole length, except at the two extremities, where it is connected by the quoins with the end walls, and held fast by them. It bends into a curve, therefore, along its length, bowing outwards most at the top and centre of length, and receiving several fractures $mmm$, approaching to vertical in direction, owing to the length of the curve being greater than that of the originally straight wall. The whole bond of the materials is more or less disturbed; but the force of the shock may only be such, as to thus curve and fracture, but not overthrow the wall. The wall $hk$ in like manner is urged forward at the ends $h$ and $k$ by the connection with the quoins of the end walls; but failing also in rigidity, the central part is left behind, and bent also by inertia; differing from the first case analyzed in this also, that the direction of movement impressed is not in the same direction with the wave transit, but reverse to it; so that here both side walls $ce$ and $hk$ move alike in direction, but to different extents. The greater velocity $\mathrm {V}$ is common to both, for both have their velocities impressed by the first semi-vibration of the wave; and were the nature of the connection at the quoins the same, whether the walls were forced outwards or inwards, both would, cœteris paribus, be bowed alike. From the nature of the quoin bond of masonry, however, the end walls at the quoins offer much less resistance to the wall $ce$, being forced outwards, than they do to the wall $hk$, being forced inwards, the quoin stones bonded into both wails finding a better fulcrum in the transverse resistance of the end walls in the latter case. The wall $ce$ in some degree resembles a beam merely supported at the two ends, while that $hk$ is partially in the condition of one encastré at both ends, both being subjected to transverse strains; and accordingly the latter usually presents the characteristic curve of double curvature when looked at in plan upon top, as in Fig. 29.

The difference in result is practically not great, but sufficient generally, to cause the side wall first moved by the wave, to have a greater curvature than the opposite one, both being more or less fractured. When the shock is of sufficient force, however, the wall $ce$ is quite overthrown, falling outwards, and tearing away from the end portions, in an irregular, sloping, and hollow curve, following along the joints, so that the detached mass is in the form in the section in line $ss$ looking towards $ce$. This seldom happens, when the wall $hk$ is devoid of intermediate support, without its being more or less prostrated likewise. This form of fracture is seen in two of the walls in the Photog. (No. 30) of overthrown houses at Polla, though unfortunately somewhat masked by the effects of the falling walls having been in this instance precipitated upon and against others.