Light waves and their uses/Lecture I
LECTURE I
WAVE MOTION AND INTERFERENCE
Science, when it has to communicate the results of its labor, is under the disadvantage that its language is but little understood. Hence it is that circumlocution is inevitable and repetitions are difficult to avoid. Scientific men are necessarily educated to economize expression so as to condense whole sentences into a single word and a whole chapter into a single sentence. These words and sentences come to be so familiar to the investigator as expressions of summarized work—it may be of years—that only by considerable effort can he remember that to others his ideas need constant explanation and elucidation which lead to inartistic and wearying repetition. To few is it given to combine the talent of investigation with the happy faculty of making the subject of their work interesting to others. I do not claim to be one of these fortunate few; and if I am not as successful as I could wish in this respect, I can only beg your indulgence for myself, but not for the subject I have chosen. This, to my mind, is one of the most fascinating, not only of the departments of science, but of human knowledge. If a poet could at the same time be a physicist, he might convey to others the pleasure, the satisfaction, almost the reverence, which the subject inspires. The æsthetic side of the subject is, I confess, by no means the least attractive to me. Especially is its fascination felt in the branch which deals with light, and I hope the day may be near when a Ruskin will be found equal to the description of the beauties of coloring, the exquisite gradations of light and shade, and the intricate wonders of symmetrical forms and combinations of forms which are encountered at every turn.
Indeed, so strongly do these color phenomena appeal to me that I venture to predict that in the not very distant future there may be a color art analogous to the art of sound—a color music, in which the performer, seated before a literally chromatic scale, can play the colors of the spectrum in any succession or combination, flashing on a screen all possible gradations of color, simultaneously or in any desired succession, producing at will the most delicate and subtle modulations of light and color, or the most gorgeous and startling contrasts and color chords! It seems to me that we have here at least as great a possibility of rendering all the fancies, moods, and emotions of the human mind as in the older art.
These beauties of form and color, so constantly recurring in the varied phenomena of refraction, diffraction, and interference, are, however, only incidentals; and, though a never-failing source of æsthetic delight, must be resolutely ignored if we would perceive the still higher beauties which appeal to the mind, not directly through the senses, but through the reasoning faculty; for what can surpass in beauty the wonderful adaptation of Nature's means to her ends, and the never-failing rule of law and order which governs even the most apparently irregular and complicated of her manifestations? These laws it is the object of the scientific investigator to discover and apply. In such successful investigation consists at once his keenest delight as well as his highest reward.
It is my purpose to bring before you in the following lectures an outline of a number of investigations which are based on the use of light waves. I trust I may be pardoned for citing, as illustrations of these uses, examples which are taken almost entirely from my own work. I do this because I believe that I shall be much more likely to interest you by telling what I know, than by repeating what someone else knows.
In order to discuss intelligently these applications of light waves, it will be necessary to recall some fundamental facts about light and especially about wave motion. These facts, though doubtless familiar to most of us here, need emphasis and illustration in order that we may avoid, as far as possible, the tedious repetition against which we were warned.
Doubtless there are but few who have not watched with interest the circular waves produced by a stone cast into a still pond of water, the ever-widening circles, going farther and farther from the center of disturbance, until they are lost in the distance or break on the shore. Even if we had no knowledge of the original disturbance, its character, in a general way, might be correctly inferred from the waves. For instance, the direction and distance of the source can be determined with considerable accuracy by drawing two lines perpendicular to the front of the wave; the source would lie at their intersection. The size of the waves will give information concerning the size of the object thrown. If the waves continue to beat regularly on the shore, the disturbance is continuous and regular and, if regular, the frequency (i. e., the number of waves per second) determines whether the disturbance is due to the splash of oars, to the paddles of a steamer, or to the wings of an insect struggling to escape.
In a precisely similar manner, though usually without conscious reasoning about the matter on our part, the sound waves which reach the ear give information regarding the source of the sound. Such information may be classified as follows:
1. Direction (not precise).
2. Magnitude (loudness).
3. Frequency (pitch).
4. Form (character).
Light gives precisely the same kinds of information, and hence it is only natural to infer that light also is a wave motion. We know, in fact, that it is so; but before giving the evidence to prove it, it will be well to make a little preliminary study of the chief characteristics of wave motion.
One of the difficulties encountered in studying wave motion is the rapidity of the propagation of the waves. A fairly moderate speed is attained by the waves propagated along a spiral spring. If one end of such a spring be fastened to a wooden box on the wall of the lecture-room, while the other end is held in the hand, we can see that any motion communicated by the hand is successively transmitted to the different parts of the spring until it reaches the wall. Here it is reflected back toward the hand, but with diminished amplitude. We can also see that any kind of transverse motion, i. e., motion at right angles to the length of the spring, whether regular or irregular, gives rise to a corresponding wave form which travels along the spring with a velocity that is the same in every case.
If the spring be very suddenly stretched or relaxed, a wave of longitudinal vibrations passes along it, announcing its arrival at the other end by a sound at the box; the time occupied in the passage being perceptibly less than that required for the transverse wave.[1]
The velocity of the wave is in both cases too great to admit of convenient investigation. In order to familiarize the student with wave 
FIG. 2motion, a number of mechanical devices have been constructed, such as that shown in Fig. 1. Such mechanical models imitate wave motions rather than produce them. They are purely kinematic illustrations, and not true wave motions; for in the latter the propagation is determined by the forces and inertias which exist within the system of particles through which the wave is moving.
The wave model of Lord Kelvin is free from this objection. It consists of a vertical steel wire on which blocks of wood are fastened at regular intervals. It is very essential that these blocks should not slip on the wire, and this end is best accomplished by bending the wire, in the middle of each block, around three small nails, as shown in Fig. 2. For the sake of symmetry two such pieces may be fastened together, with the wire passing between them. Attention may be fixed upon the motion of the ends of the blocks, by driving into them large, gilt, upholstering tacks—a device which adds considerably to the attractiveness of the experiment. The complete apparatus is shown in Fig. 3.
On giving the lowest element a twist, the torsion produced in the wire will communicate the twist to the next element, etc. The twist thus travels along the entire row, 
FIG. 3moving more slowly the smaller the wire and the heavier the blocks, so that, by varying these two factors, any desired speed may be obtained.
The wave form which is propagated in any of the various possible cases is, in general, very complicated. It can be shown, however, that it is always possible to express such forms, however complex, by a series of simple sine curves such as that represented in Fig. 4. The study of wave motion may be much simplified by this device. Accordingly, in all that follows, except where the contrary is expressly stated, it will be assumed that we are dealing with waves of this simple type.
There are certain characteristics of wave motion of which we shall have to speak frequently in what follows, and which therefore need definition. In the first place, the shape of the wave illustrated in Fig. 4 is important. It is the curve which would be drawn by a pendulum, carrying a marker, upon a piece of smoked glass moving uniformly at right angles to the motion of the pendulum. Since the pendulum moves in what is called simple harmonic motion, the curve is called a simple harmonic curve, or a sine curve. The amplitude of the wave is the maximum distance of a crest or a trough from the position of rest, i. e., from the straight line drawn through the middle of the curve. The period of the vibration is the time it takes one particle to execute one complete vibration; i. e., to revert to the pendulum, it is the time it takes the pendulum to execute one complete swing.[2] The phase of any particle along the curve is the portion of a complete vibration which the particle has executed. The wave length is the distance between two particles in the same phase. Thus it is the distance 
FIG. 4between two consecutive crests or between two consecutive troughs. When all the particles vibrate in one plane, e. g., the plane of the drawing, the wave is said to be polarized in a plane. The velocity of propagation of the wave is the distance traveled by any given crest in one second.
As has just been stated, the type of wave motion illustrated in Fig. 4 may be approximately realized by imparting the motion of a pendulum or a tuning-fork to one end of a very long cord. It can be shown that after a time every particle of the cord will vibrate with precisely the 
FIG. 5same motion as that of the pendulum or tuning-fork from which the disturbance starts. Any particular phase of the motion occurs a little later in every succeeding particle; and it is this transmission of a given phase along the cord which constitutes the wave motion.
Very elementary considerations show that the length (l) of the wave is connected with the period (p) of vibration of the particles (the time of one complete cycle) and the velocity (v) of transmission by the simple relation l = pv. 
FIG. 6In fact, if we could take instantaneous photographs of such a train of waves at equal intervals of time, say one-eighth of the period, they would appear as in Fig. 5. It will readily be seen that in the eight-eighths of a period the wave has advanced through just one wave length, while any particle has gone once through all its phases.
Let us next consider the superposition of two similar trains of waves of equal period and amplitude. If the phases of the two wave trains coincide, the resulting wave train will have twice the amplitude of the components, as shown in Fig. 6. If, on the other hand, the phase of one train is half a period ahead of that of the other, as in Fig. 7, the resulting amplitude 
FIG. 7is zero; that is, the two motions exactly neutralize each other. In the case of sound waves, the first case corresponds to fourfold intensity, the second to absolute silence.
The principle of which these two cases are illustrations is miscalled interference; in reality the result is that each wave motion occurs exactly as if the other were not there to interfere. The name has, however, the sanction of long usage, and will therefore be retained. The principle of interference is of 
FIG. 8such fundamental importance that it will be worth while to impress it upon the mind by a few experimental illustrations.
Fig. 8 represents an apparatus devised by Professor Quincke for illustrating interference of sound. An organ pipe is sounded near the base of the instrument. Thence the sound waves are conducted through the two vertical tubes, one of which is capable of being lengthened, like a trombone. They then reunite and are conducted by a 
FIG. 9single tube to a "manometric capsule," which impresses the resulting vibrations on a gas jet, the trembling of the jet being rendered visible in a revolving mirror.
When the two branch tubes are of equal length, the waves reach the flame in the same phase, causing it to
FIG. 10 vibrate, as shown by the character of the image in the revolving mirror, Fig. 9; while, if one of the branches be made half a wave[3] longer than the other, the disturbance disappears, and the image appears as shown in Fig. 10.
A very simple and instructive experiment may be made by throwing simultaneously two stones into still water, and a number of interesting variations may be obtained by varying the size of the stones and their distance apart.
The experiment may be arranged for projection by using a surface of mercury instead of one of water, and agitating it by means of a tuning-fork, 
FIG. 11to the ends of whose prongs are attached light pieces of iron wire which dip slightly into the mercury.
The arrangement of the apparatus is shown in Fig. 11. The light of an electric lamp is concentrated on a small mirror, by which it is reflected through a lens to the tuning-fork, whose ends dip into a surface of mercury. It is reflected by the mercury surface back through the lens and passes to another mirror, by which it is reflected to form an image on a distant screen. Fig. 12 shows the resulting disturbance of the surface. The circular ripples which diverge from the points of contact of the forks are represented by the circles. These move too rapidly to be seen in the actual experiment, but may be readily recognized in an instantaneous photograph. The heavy lines are the lines of maximum disturbance, where the two systems of waves meet, always in the same phase; while the lighter parts between represent the quiescent portions of the surface, where the crests of one system meet the troughs of the other, forming stationary waves. Fig. 13 is a photograph of the actual appearance.
Another striking instance of interference is furnished by two tuning-forks of nearly the same pitch. Take, first, two similar forks mounted on resonators. When these are sounded by a cello bow, the resultant tone may or may not be louder than the component tones, but it is constant—or, at least, dies away very slowly. If, now, one of the forks be loaded by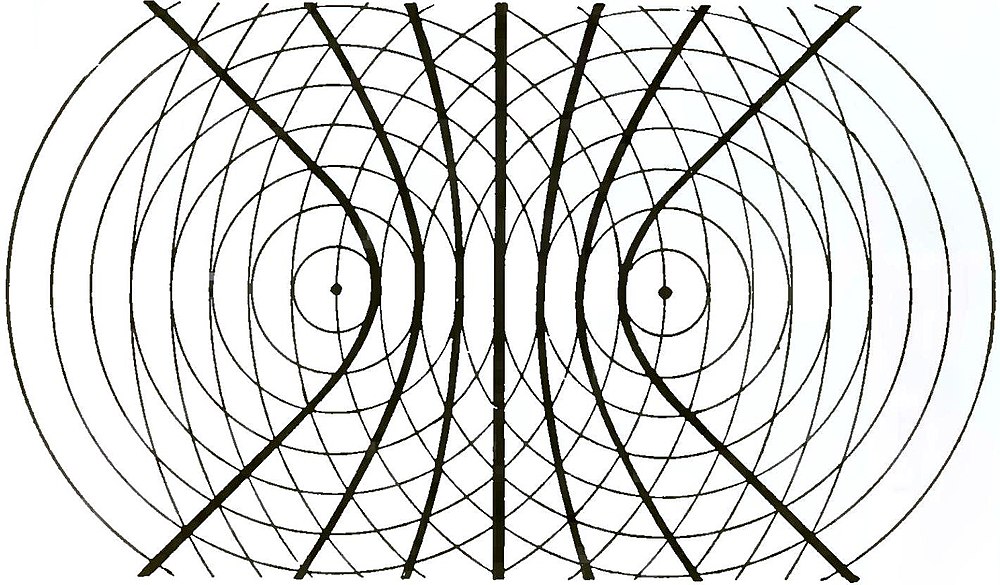 
FIG. 12fastening a small weight to the prong, the sound sinks and swells at regular intervals, producing the well-known phenomenon of "beats." The maximum occurs when the two vibrations are in the same phase. Gradually the loaded fork loses on the other until it is half a vibration behind; then there is a brief silence. This may be shown graphically by allowing each fork to trace its own record along a piece of smoked glass, and by adding the two sine curves, as shown in Fig. 14.
The matter of the interference of light waves requires special treatment on account of the enormous rapidity of the vibrations. This statement, however, inverts the actual chronology, for this rapidity is inferred from the interference experiments themselves.
A beautiful instance of such interference occurs in a soap film. Ordinarily, however, such films have the form 
FIG. 13of a soap bubble; and, while the disturbing causes usually in operation enhance wonderfully the beauty of the appearance, they do not permit the accurate investigation of the 
FIG. 14phenomenon. These disturbing elements are very much diminished in the arrangement which follows:
A soap solution is made up as follows: One part of fresh Castile soap is dissolved in forty parts of warm water; when cool, three parts of the solution are mixed with two parts 
FIG. 15of glycerine. The mixture is cooled to a temperature of 3° or 4° C., and filtered. A soap film is formed by dipping into the solution a short piece of wide glass tubing. Removing the tube and placing it so that the film is vertical, a series of beautifully colored bands appear, the colors being deeper at the top and gradually fading into barely perceptible alternations of pink and green near the bottom. The bands broaden out as the film gets thinner, but the succession of colors remains the same and may be described as follows: The top of the film is black; then the colors in the first band are bluish gray, white, yellow, and red; those in the second band are, in order, violet, blue, green, yellow, red; the third band is blue, green, yellow, and red; and the succeeding bands green and red. The colors are best observed by using the film as a mirror to reflect the light from a white wall; or the light from a lantern may be reflected to a lens which forms an image of the film on a screen.
The colors of thin films and of interference phenomena generally are among the most beautiful in nature, and while no artist could do justice to such a subject, much less a lithographic plate, such a plate (Plate II) may be used to recall the more striking characteristics.
For the scientific investigation of the interference of light waves, however, the soap film is rather unsatisfactory 
FIG. 16on account of the excessive mobility of its parts and the resulting changes in thickness. A much more satisfactory arrangement for this purpose is the following: Two pieces of glass with optically plane surfaces are carefully cleaned and freed from dust particles. A single fiber of silk is placed on one of the surfaces near the edge, and the other is pressed against it, thus forming an extremely thin wedge of air between the two plates, as shown in Fig. 16.
It will be found that in this case the succession of colored bands will resemble in every respect those in the soap film, except that they are now permanent. The light is reflected from all four surfaces, and hence the purity of the colors is somewhat dimmed by the first and the fourth reflections. These may be obviated by using wedges of glass instead of plates.
To account for the colored fringes it will be best to begin with the simpler case of monochromatic light. If a piece of red glass is interposed anywhere in the path of the light, the bands are no longer colored, but are alternately red and black. They are rather more numerous than before, and a trifle wider. If a blue glass is interposed, the bands consist of alternations of blue and black, and are somewhat narrower (cf. Plate II).
Let us suppose now that red light consists of waves of very small length. The train of waves reflected by the first surface of the film will be in advance of that reflected by the second surface. At the point where the two surfaces touch each other the advance is, of course, zero; and here we should have the two wave trains in the same phase, with a consequent maximum of light. Where the thickness of the film is such that the second wave train is half a wave behind, there should be a dark band; at one whole wave retardation, a bright band; and so on.
The alternations of light and dark bands are thus accounted for, but the experiment shows that the first band is dark instead of bright. This discrepancy is due to the assumption that both reflections took place under like conditions, and that the phase of the two trains of waves would be equally affected by the act of reflection. This assumption is wrong, for the first reflection takes place from the inner surface of the first glass, while the second occurs at the outer surface of the second glass. The first reflection is from a rarer medium—the air; while the second is from a denser medium—the glass. A simple experiment with the Kelvin wave apparatus will illustrate the difference between the two kinds of reflection. The upper end of this apparatus is fixed, while the lower end is free; the fixed end, therefore, represents the surface of a denser medium, the free end that of a rarer medium. If now a wave be started at the lower end by twisting the lowest element to the right, the twist travels upward till it reaches the ceiling, whence it returns with a twist to the left—i. e., in the opposite phase. When, however, this left twist reaches the lowest element, it is reflected and returns as a twist to the left—so that the reflection is in the same phase.
There is thus a difference of phase of one-half a period between the two reflections, and, when this is taken into account, experiment and theory fully agree. We may now make use of the experiment to find a rough approximation to the length of the light waves.
If we measure by the microscope the diameter of the filament which separates the glasses, it will be found to be, say, two and seven-tenths microns.[4] Counting the number of dark bands in red light, we find there are eight; and hence we conclude that at the thickest part of the air film the retardation is eight waves, and hence the distance separating the glasses—that is, the thickness of the filament—is four waves, which gives about sixty-eight hundredths of 
FIG. 17a micron for the wave length of red light. If blue light is used, there will be twelve dark bands, whence the wave length of blue light is forty-five hundredths of a micron.
The following table gives the approximate wave lengths of the principal colors:
|
Red
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
0.68 microns |
|
Orange
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
.63 microns„ |
|
Yellow
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
.58 microns„ |
|
Green
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
.53 microns„ |
|
Blue
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
.48 microns„ |
|
Violet
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
|
.43 microns„ |
Fig. 17 gives a diagram of the wave lengths of the different colors, magnified about twenty thousand times.
SUMMARY
Waves give information concerning direction, distance, magnitude, and character of the source. Light does the same; hence the presumption in favor of the hypothesis that light consists of waves.
Wave trains may destroy each other by "interference." Light added to light may produce darkness.
The reason why interference is not more frequently apparent in the case of light is that light waves are exceedingly minute.
By the measurement of interference fringes it is possible to measure the length of light waves, and the results of such measurements show that the wave lengths are different for different colors.
- ↑ I am indebted to Professor Cross for this illustration.
- ↑ In some works the half of this is taken, i. e., the time it takes a pendulum to move from the extreme left to the extreme right.
- ↑ The length required will depend on the tone of the organ pipe. For middle C (256 vibrations per second) the double length required is two feet.
- ↑ A micron is a thousandth of a millimeter, or about a twenty-five thousandth of an inch.