Methods of Operating the Comptometer
INDEX.
| To Set the Machine at Naught | 1 |
| Explanation of the Key-Board | 1 |
| Addition | 1-4 |
| Not Necessary to Strike Keys in Regular Order | 2 |
| How to Finger the Keys | 3 |
| Finger Exercise | 4 |
| Position Illustrated | 4 |
| Multiplication | 5-10 |
| Proper Key Strokes | 5 |
| Colored Diagram of Key Strokes | 6 |
| Explanation of Diagram | 7 |
| Position of Hands for | 8 |
| Two Finger Method | 9 |
| Where the Sum to be Multiplied Stands on the Register of Machine | 9 |
| Where the Multiplier Consists of Two Figures and the Multiplicand is Already on the Machine | 9 |
| Multiplying High Decimals | 10 |
| The Red Figures | 11 |
| Subtraction | 12 |
| Correcting Mistakes | 12 |
| Division | 13-21 |
| Rule for Small Divisors | 13-17 |
| Position of Hands for | 18 |
| Rule for Large Divisors | 18 |
| Dividing High Decimals | 21 |
| Common Fractions | 22 |
| Stone Measure | 23 |
| British Exchange | 24-28 |
| Addition of | 24-25 |
| Reduction of United States Money to | 26 |
| Table for Reducing | 27 |
| Reducing United States Money to | 26-28 |
| Interest | 29 |
| Discounts | 30 |
| Compound Interest | 31 |
| Square Root | 32-33 |
| Equations | 34 |
PRICE OF THIS BOOK $5.00.
COPYRIGHT 1895, BY FELT & TARRANT MFG. CO.
Preface.
Anyone knowing the meaning of common mathematical terms, such as dividend, product, etc., can learn how to perform on the Comptometer any of the classes of examples explained in this book in a few minutes. It is very easy to learn how, but it is to have skill of the fingers that is most necessary. The Comptometer is not a hand organ or grind stone. Being a key-operated instrument, like the typewriter, it requires considerable practice to render one sufficiently skillful to operate it successfully. Addition requires more practice than anything else. Multiplication requires comparatively little, but care must be taken to follow the methods laid down in the book, because there are other methods which one is apt to stumble onto which are not nearly so rapid. Division is more difficult to learn, but easy to remember, and though it requires more practice than multiplication, it does not require nearly as much as addition. To those who think they are so gifted that they can learn to operate the Comptometer with little or at least much less practice than is necessary for common mortals, we will say, do not undertake to learn the Comptometer at all. You will not succeed. Nothing but faithful practice will enable anyone to become an operator. You may say that you learned to use the typewriter skillfully in a few days, but that is impossible. No one ever did. After a few days' practice one may be able to operate slowly, but not as they would be expected to operate to fill a position as a regular operator. There is nothing in this world worth knowing, no skill worth having, which does not cost study or practice.
The Comptometer requires practice.
A stenographer finds it necessary to be a good typewriter operator and a book-keeper finds it advantageous to be a good Comptometer operator, which he can by using it twenty minutes a day for sixty or eighty days on his regular work.
Overlooking the fact that it takes practice to do anything well which is worth doing, some assume that they are operators before they can "operate" a little bit, and ascribe the resulting inefficiency in the combination (machine and operator) to the machine, when it should be ascribed to the operator, and when a few weeks' use of the machine would remove that inefficiency.
Some not only do not practice long enough, but fail to obtain a correct understanding of the methods for operating, and therefore jump to the conclusion that it is not adapted to their particular work, when there are hundreds using it on precisely the same work at a large saving of time and trouble. We will be glad to write special instructions for anyone who will send us a sample example in their principal work. This book is not intended to give the short cuts on the Comptometer, which can be employed on almost every kind of special work.

Oil.
If used only once or twice a week, oil about once in six months. If used eight hours a day right along by a rapid operator, oil about once in two weeks.
Put only a couple of drops each side of each numeral wheel through top corner of square holes in the register plate. Use any good typewriter or sewing machine oil.
Methods of Using the Comptometer.
Do not try too complicated examples, such as interest, exchange, square root, etc., until thoroughly familiar with handling the keys in the operations of subtraction, multiplication and division.
Always depress each key as far as it will go, and never depress two keys at the same time, but allow one to come back to its place before another is depressed.
To set the machine at naught, depress the lever on the right of the machine with the third finger of the right hand and turn the knob from the operator a little. Then release the lever, and continue to turn until the machine stops.
Explanation of the key-board. It will be observed that there are two figures on each key, one a large black one and the other a small red one. The black ones indicate the keys to be struck in addition and multiplication, and the red ones, those to be struck in division and subtraction.
In speaking of the keys, those running in a line up and down are called a column, and those running in a line from left to right are called a row. Thus all the keys having a large 4 on top stand in a row and are called the row of 4s.
In explaining the key-board for addition and multiplication, the keys are called by the black figures on their tops. Beginning at the right of the machine, the first column running from 1 to 9 represents units; the second column, tens; the third, hundreds; the fourth, thousands, etc. Thus the 7 key in the fifth column indicates 70000, and the 3 key in the second column indicates 30; therefore, to strike 467 on the machine, depress the 4 key in the third column, the 6 key in the second column, and the 7 key in the first or units column; 467 will then be indicated on the register of the machine. This number being left on the register and some other being struck as, for example, 3261, the register will show the sum of the two numbers; in this case, 3728.
Addition.
Many users of the Comptometer, after several months' practice, become so familiar with the key-board that they do do not look at the keys at all when adding. Therefore we make the tops of every other row of keys concave, so that one can instantly tell by the feeling which row he is striking. All the keys standing for odd numbers have concave tops, and all standing for even numbers have flat tops. It requires considerable practice to acquire sufficient skill to enable one to use the Comptometer rapidly and accurately on addition. It is not to know how, but it is to acquire skill of the fingers, which requires practice. In this respect it is precisely like the typewriter.
Twenty minutes' use of the Comptometer each day for sixty days will develop more speed than sixty hours' practice all in a few days. It requires more practice to perform addition rapidly than it does to do any other class of examples. Doing actual work is the only practice that is good for anything. But as addition constitutes the bulk of mathematical work, the Comptometer is used for addition more than for anything else. One should not try to do all their practicing of addition in one day, but use the machine twenty minutes each day for several weeks, when they will find that they can easily add with the Comptometer more rapidly and correctly than any two men can mentally. Do not imagine that you can estimate what you will be able to do after more practice, when you have only practiced ten days, for at that time you will just be beginning to learn how to use the machine, although you may think yourself quite an operator.
To perform addition, it is necessary merely to strike each number on the machine and the total will be indicated on the register.
It is not necessary to strike the figures in regular order, but for convenience and speed it is better to strike the small figures in each number before striking the larger ones. Thus: In striking the number 263, first, with the first finger, strike 2 in the third column; next, with the third finger, strike 3 in the first column; with the second finger, strike 6 in the second column. The movement of the hand back and forth over the key-board several times is thus avoided, and the key next to be struck is always exposed to view.
Strike each key firm and distinct, raising the finger clear up before putting another finger on another key. Always begin at the top and add downward. Point the place on the paper with the index finger of the left hand. Only take three columns at a time; read the three figures, and then look at the key-board while striking the first two, and read the next three figures while striking the last one of the preceding three. Use the first finger for the hundreds column, the second for the tens column, the third for the units column. Do this every time, so that each finger has one column to attend to, and there is no movement of the hand from left to right and from right to left. When three columns are added, move the hand over on the keys and take the next three columns. Speed in addition comes only from practice on actual work. Twenty minutes a day for sixty days will make a fair speed, and from that on the speed will continue to increase for a year or more.
Some prefer to use four fingers and carry four columns at a time. If one finds the little finger handy it is well to do so. Others prefer to carry all the columns at once, and it is always best to do so when adding scattered items, or direct from checks also when adding cross footings.
We give a few finger exercises on next page, which, if practiced, will help in obtaining control of the muscles of the fingers and familiarize the fingers with the key-board. The key-stroke on the Comptometer is different from that required on a typewriter, therefore typewriter operators will have to learn to give it the proper and natural stroke. On a typewriter the touch must be a quick blow, for the typehead is used as a hammer to strike the impression; but on the Comptometer the touch required is a natural quick downward stroke, not a blow.
Finger Exercise.
|
|
|

Position of Hands for Addition.
Always begin at the top of the column and add downward, keeping the index finger of the left hand where it points to the next item to be added.
Multiplication.
In multiplication the first thing is to acquire the habit of rapidly giving the keys the proper stroke a number of times in succession. Therefore practice for fifteen minutes the following finger exercises:
Place the second finger of the right hand on the 7 key and strike it four times; move to the 70 key and strike it four times, and continue clear across the machine, striking each 7 key four times. Let the finger raise off of the key one-quarter inch each stroke, not much more or less. Strike them just as rapidly as possible, always giving a full stroke. After practicing on the 7 keys a few minutes, take the 5 keys, then the 9 keys, then the 2 keys. Then begin on the 7 keys again and strike the first one six times, the next one four times, the next one six times, the next one four times, and so on across the row. Do this on some of the other rows.
In multiplying, keep the eyes on the paper and not on the machine. By keeping the eyes on the paper the accuracy and rapidity of the work will be increased 100 per cent. It is advisable to glance at the keys each time a new figure of the multiplier is employed, but not when moving from one key to another in the same row.

2253×84.
Multiplication.
Multiplication.
Its Simplicity as done on the Comptometer illustrated by diagram.
Copyright 1894, by Felt & Tarrant Mfg. Co.
RULE.—Begin at the right of the rows of keys indicated by the first figure of the multiplier, and strike each successive key in the same row towards the left as many times as indicated by the corresponding figure in the multiplicand. Proceed with each figure of the multiplier as with the first, beginning always in the column of keys in which the figure of the multiplier stands.
Explanation of Diagram.
See black lines descending from arrows on cut. Each line represents a stroke on the key in performing the following example: Example 2253×84. Because 4 is the first figure of the multiplier, begin on the first key of the row of 4s and strike the first one three times, the second one five times, the third one two times and the fourth one two times—that is, strike each key in succession the number of times indicated by the corresponding figure of the multiplicand (2253).
8 being the second figure of the multiplier, begin on the second key in the row of 8s and strike three times, move to the next key to the left and strike five times, etc., etc., when the answer, 189252, is shown on the register in front. (See cut.)
Observe that in multiplying the finger only moves from one key to its next neighbor, therefore keep the eyes on the paper, not on the keys. (See finger exercises on page 5 and proper position of hands on page 8.)

Position of Hands for Multiplication.
Noting the first figure of the multiplier, place one finger of the right hand on the proper key and then, keeping the eyes on paper, without even glancing at the machine, strike each succeeding key, as explained in the rule and diagram.
After a little practice one can try the two-finger method of multiplying, in which the position of the finger is the same as for division. (See page 9.)
Two-finger Method of Striking the Keys.
After a little practice one can carry two figures of the multiplier at once with the index finger of each hand, striking alternately, and by so doing increase the speed 50 per cent.
Considerable time can with profit be devoted to the following finger exercises, because two fingers are used a great deal, especially in division and multiplication. In practicing this method run fast, do not be too cautious, and you will soon acquire the right stroke.
Strike 74,000,000 five times, using the index finger of the left hand in striking the 7, and the index finger of the right hand in striking the 4; striking them alternately, allowing one finger to be raised entirely off one key before depressing another; raise the fingers one-fourth of an inch off the keys each stroke. Move both fingers one key to the right and strike five times; continue moving to the right one column at a time across the machine, striking the keys five times each. Do the same thing with 36, 45, 63, 54, 18, 81, 92, 47 and 58. At first it will be difficult to strike the keys rapid and also each independently and in proper time. It is to teach this, the proper key stroke, that this exercise is given. Avoid the tendency to strike keys in jerky time like this, .. .. .. .. .. .. but strike them regular like this......................
Where the sum to be multiplied stands on the register of the machine, and the multiplier is not greater than 9, to avoid taking it off, it can be conveniently multiplied by using the number one less than the multiplier, for example: we are required to obtain 4263 x 64 x 8. After multiplying 4263 by 64 as illustrated above, 272832 appears on the register as the result. To multiply this amount by 8, without turning the machine to naught, take the row of keys next lower than 8 the multiplier, (the 7's,) and beginning at the left of the multiplicand over the hundreds of thousands, strike twice, as 2 is in that order on the register; then moving to the right one column, strike seven times, as 7 is in that order; two times in the next order to the right, as 2 is in that order, etc., until all the keys have been struck as many times as the corresponding figures on the register indicate. The product, 2182656, will then appear on the register.
Where the multiplier consists of two figures and the multiplicand is already on the machine, deduct one from the multiplier and then proceed to strike it on the keys by striking each figure of the multiplier alternately (using the index finger of each hand), and working from the left of the multiplicand just the same as in the example illustrated above.
Where one factor is on the machine and the other consists of three or more figures, the following method will be found advantageous. In this rule we will call the number standing on the register of the machine the multiplier and the one not on the machine the multiplicand.
Observe the figure which stands in the highest order of the multiplier; place the finger on the key representing that figure and standing in the same column; strike it one time less than is indicated by the first figure on the right of the multiplicand; move one key to the left and strike it as many times as is indicated by the next figure of the multiplicand. Continue to strike each succeeding key to the left as many times as is indicated by the corresponding figure of the multiplicand. Observing the figures standing in the next highest order on the machine, proceed the same as with the first.
Example: 17+(4×30)+(360×2)×2,743. First add 17; then without turning the machine to naught, multiply 30 by 4, then 360 by 2, when the sum of all these operations, 857, will have accumulated on the register of the machine. The next step is to multiply 2,743 by 857, which stands on the register. As 8 stands in the highest order on the register, (third column), place the finger on the 8 key of that column and strike it two times, as two is one less than three which is the right hand figure of the number 2,743. Then move one key to the left and strike four times; moving one more key to the left, strike seven times, and again moving one column, strike two times. The next figure of the multiplier is 5 and stands in second column. Therefore, place the finger on the 5 key of that order and strike two times; move to the left one column and strike four times, etc. Proceed with the last figure of the multiplier, which is 7, the same as with the first two, when the answer, 2,350,751, will appear on the register.
In multiplying examples in which high decimals occur it is desirable to reverse the system of striking the keys and work from the left to the right. By doing so, examples which would otherwise be too large for an eight column machine can be computed. Thus: 486.34286 X 75.8763. Begin on the highest key in the row of 7's and strike it four times; move one key to the right and strike eight times, etc. The answer expressed on the register will be 36901.8952 which is correct to the second decimal place.
It is obvious that when decimal fractions occur in any kind of computations, all that is necessary is to point off in the usual way.
Where high decimals are used and the keys are struck from the left, point off as many holes from the left as there are places to the left of the points in the multiplicand and multiplier. There is one hole to the left of the highest column of keys, therefore, with the product of 2.487634×3.24692 we would have 08.07+ and with the product of 8.76321×6.76342 we would have 59.26+.
The Red Figures.
Directions for using the Red Figures.—In performing division or subtraction, both the black and the red figures are used to indicate the keys to be struck, and for convenience of explanation, the black figures will be named positive, and the red figures negative. The red figures are small and the black ones large.
When it is not specified whether the keys are positive or negative, it is to be understood that they are positive.
When striking the keys negative (according to the small figures), we always strike one less than the number itself, except that if there be ciphers on the right, deduct one from the nearest number to the right. Thus, in using the small figures, we would strike 83 for 84, 126 for 127, and 340 for 350, etc., etc. On the keys themselves the small figures are colored red and the large figures black, making the difference conspicuous.
When a number to be struck negative has a cipher or ciphers on the right, before deducting the 1, such ciphers must be disregarded in striking the keys, but when the ciphers occur between digits, they must be struck the same as the digits. Thus, in the number 1450, strike 1, 4 and 4 in the fourth, third and second series respectively, and pay no attention to the cipher in the units series. But should the number given be 1508, 1, 5, 0 and 7 must be struck on the keys.
It will be observed that there are no keys having the figure 9 in red. Wherever the figure 9 occurs in the number remaining after deducting the one, it is to be disregarded in striking the keys according to the red figures. Thus, to strike 5963, the red 5 must be struck in the fourth column of keys, and as 9 stands in the third order, we do not strike any key in the third column, but strike six in the second column, and two in the first or unit column.
Should the right hand figure of a number to be struck negative be "1," the cipher remaining after deducting one must be struck: as, for example, if 1561 is to be struck negative, after deducting one, the number 1560 will remain, each figure of which must be struck, including the cipher. Subtraction.
Strike the minuend positive and the subtrahend negative, see page 11.
A row of cut offs by which the carrying of any column can be stopped at will, have been put in front of the keys. They are for use in subtraction and in correcting mistakes. Do not try to subtract a number from one smaller than itself; for instance in the example, 2114-18; as 18 cannot be substracted from 14, push back the cut off just above the third column and strike 017 according to the red figures.
In examples like 183-45, push back the cut off above the second column and strike 44 on the red figures.
Example: Find the value of 4286-262. After striking 4286 positive strike 262 negative while holding back the cut off between the third and fourth columns. The red figures to be struck are, therefore, 2, 6, and 1. The number 4024 will be then indicated on the register, as the remainder.
Correcting Mistakes.
One seldom strikes a wrong key without noticing it before completing the stroke, and can immediately rectify the mistake by striking a key in the same column which is the same distance from the other end of the column while holding back the proper cut off. Thus: If the 8 key in the thousands column is struck by mistake, it being the second key from the back end of the column, strike the second key from the front end of that column.
If several keys are struck by mistake, simply subtract the amount which they represent and proceed as though no mistake had been made. Thus: Suppose 1783 had been struck, strike 1782 according to the red figures in the same columns while holding back the proper cut off, and the amount on the register will be the same as though no mistake had been made.
Division.
Its Simplicity as done on the Comptometer illustrated by diagram.
COPYRIGHTED 1894, BY FELT & TARRANT MFG. CO.
RULE.—Strike the dividend on the keys according to the large figures on their tops.
Then place the fingers on the keys for the divisor—less 1—according to the small figures on their tops, in the columns embracing on the left of the dividend the least number of places which, by themselves, represent an amount as large or larger than the divisor and strike repeatedly until the number of strokes agree with the figure in the next column to the left of that on which the keys are being struck, and then continue striking until those columns of the register in which the keys are being struck represent an amount less than the divisor;[1] after which the left hand figure on the register is the first quotient figure.
Then move the fingers one column to the right and proceed to find the second quotient figure in the same manner and so on until all the quotient figures have been obtained.
Point off from the right as many places as there are places in the divisor, when the figures at the left will be the quotient and those at the right the remainder.
NOTE.—Do not worry about why the above process brings the answer. It is simply an arbitrary rule, by which any and all examples in division can be computed on the Comptometer, and once understood is so simple that it cannot be forgotten. All there is to it is that you strike the divisor on the keys just as many times as indicated by the figure in the "next place to the left in the register" and then if the remainder is larger than the divisor strike the keys again one or more times until the remainder becomes smaller than the divisor. Twenty key strokes, all on eight keys, perform the following example, to do which only requires five seconds. No guessing how many times the divisor is contained as when computing mentally, for on the Comptometer every step is positive and assured. The machine tells you how many times to strike the keys, and after you have struck them it tells you what the answer is.

Example: 2952÷84.
First strike the number to be divided (2952) according to the large figures on the keys, which will cause it to show in the register as above.
The divisor (less 1) is always struck according to the small figures on the key tops. [2]Therefore, we place our fingers on the small 8 and on the small 3 over the units and tens of 295 in the register as shown above, because the two left hand figures of the dividend (29) represent an amount smaller than the divisor (84) otherwise we would place the fingers on keys small 8 and small 3 over the 29. 
Having the fingers on the keys, as shown above and explained under preceding cut, we strike them twice, because 2 stands in the next column in the register to the left of the column of keys on which the fingers are placed (see register fourth column preceding cut) but after striking the keys twice 3 appears (as shown by above cut) where the 2 was (preceding cut) so strike once more, making three times, because in division the keys must always be struck the number of times indicated by the figure showing in the next column to the left of the columns in which the keys are being struck.[3]
After striking the keys three times, for the reasons specified, we have 3 as our first quotient figure and 43 as our first remainder, as shown above.

Having obtained the first quotient figure, we now move our fingers one column to the right (as shown above) and find the second quotient figure in the same manner that the first one (3) was found.
Because 4 shows in the register, (see register third column preceding cut) next column to the left of those on which the fingers now rest, strike four times, after which we have a remainder of 96. Therefore, strike again because the remainder (96) is larger than the divisor (84) after which 5 shows as the second quotient figure and 12 as the remainder, as shown above.
Point off from the right two places because you have two places in the divisor, and the final answer, 35+12, shows on the register.

Position of Hands for Division.
In dividing keep the eyes on the register, not on the keys. There is no occasion to look at the keys after the fingers are once placed. After once understanding division and obtaining a little practice, strike the keys in rapid succession. Where one hesitates it is because of habit acquired in learning, not because of any necessity of proceeding carefully.
- ↑ It is obvious that if 0 be in the next column to the left, you strike only to reduce those columns of the register in which the keys are being struck to an amount less than the divisor.
- ↑ See page 11 and page 17. The large figures show what keys to strike when adding, multiplying, computing interest, etc., etc., and the small figures which to strike when subtracting, dividing, exacting square root, figuring discounts, etc., etc. It is obvious that where there are ciphers on the extreme right of the divisor they are disregarded except in pointing off for the remainder. Thus, if the divisor be 4700 divide just the same as though it was 47 and stop dividing as soon as the quotient figure in the fifth place from the right in the register is obtained, and point off four places. That is, do not strike any keys for the divisor on the two right hand columns of the machine. The figure in the next column to the left is always a check on the accuracy of the work. If you have struck the keys five times and the figure in the next column to the left is 4, you have struck them once too much, so push back the cut off next above the keys struck and add the divisor once. In using large divisors, especially where high decimals are used, set the dividend on the left of the machine, so that it can be carried out decimally if desired. Where either the divisor or dividend, or both, are decimals, set the dividend on the left of the machine, and if there be one more place to the right of the point in the dividend than there are to the left of the point in the divisor turn down the second pointer from the left of the machine, if two more turn the third pointer, etc., then proceed to divide, and the decimal point in the quotient will be where the pointer is turned down. If there is one more place to the left of the point in the divisor than in the dividend, the decimal point in quotient is to the left of the highest hole of the register. If two more places to the left of the point in the divisor than in the dividend, the point is one place to the left of the highest hole of the register, etc. etc.
- ↑ See page 17. In other words, the figure in the register first column to the left of the keys being struck always tells how many times to strike the keys. If, in the case above illustrated, the figure in the fourth column of the register had been 5 instead of 3 we would have struck the keys five times instead of three times. Generally, after you start striking the keys the "next figure, to the left," will change, but always keep right on striking the keys until the number of strokes on the keys agrees with it. It never changes so as to require more than nine strokes on the keys. In striking the divisor, strike each key alternately allowing one finger to be raised entirely off one key before depressing the other.
Special Rule, Illustrated by Diagram, for Using Large Divisors on the Comptometer.
COPYRIGHTED 1894, BY FELT & TARRANT MFG. CO.
The regular rule, illustrated on pages 13-17, for computing division, applies to all examples, large or small, but where the divisor exceeds three or four places the following modification of the regular method is more convenient, because, by this modification, the fingers do not have to handle more than two keys at a time. It is also more simple for, by it, only keys in rows are used (except for the two left hand or trial figures of the divisor) the same as in multiplication.
It is useless for one to attempt to divide by this process until the regular process on pages 13-17 is thoroughly understood.
Rule:—Find a quotient figure by using the two left hand figures of the divisor, and then, on the row of keys on which the "large key figure" is the same as the quotient figure, strike for each of the remaining figures of the divisor; thus, suppose a remaining quotient figure to be 6, count "six, seven, eight," striking each time, which, of course, is three times altogether. Or, suppose the remaining quotient figure is 4, count "four, five, six, seven, eight." Always start counting with the figure and stop at eight, except for the extreme right hand figure which must be struck once extra.
NOTES.—If either of the two left hand figures of the divisor be 9, use the first three figures as a trial divisor, because that column in which 9 stands does not have to be struck at all.
If any of the "remaining" figures of the divisor be 9, of course no counts of strokes are made for it unless it is the units figure (last figure) of the divisor when one stroke is given.
If there be a naught (0) among the remaining figures of the divisor count "naught, one, two, three," etc., just the same as for any figure.
In obtaining a quotient figure with the trial divisor it sometimes occurs that the remainder resulting from dividing by the trial divisor nearly equals the trial divisor, and that, striking for the "remaining" figures of the divisor, increases the remainder, until it becomes as great or greater than the trial divisor. In such cases, strike the entire divisor on the keys according to the red figures; this will increase the quotient figure and reduce the remainder.

Example:— 90892150÷3567648.
Striking the dividend on the machine and then using 35 (according to the small figures on the keys) as a trial divisor, two strokes show that the first quotient figure is 2; therefore, move the right hand finger one column to the right on the large 2 key. The first of the remaining figures of the divisor (67648) being 6, count thus: "six, seven, eight," striking the key each count; (the next "remaining" figure being 7) move to the next 2 key and count "seven, eight," striking each count; move one key to the right and count "six, seven, eight," striking each count; move one key to the right and count "four, five. six, seven, eight;" move one key to the right and count "eight," but this being the last figure strike one time more. See Fig. A.
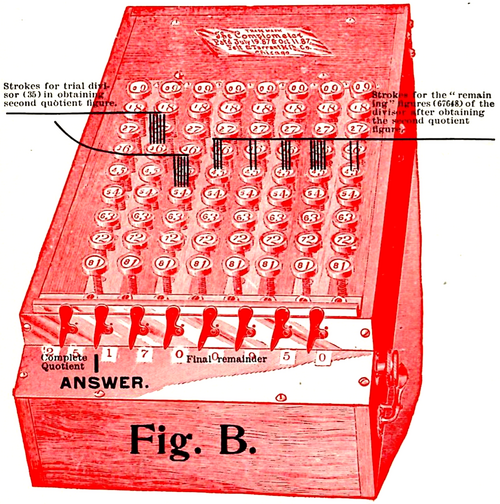
Again using the two left hand figures as a trial divisor we find that the second quotient figure is 5, so put right hand finger on the large 5, one column to the right and count "six, seven, eight," move to the right and count "seven, eight," and so on for each of the remaining figures of the divisor, when pointing off we have 25+1700950. See Fig. B.
It will be seen that, if desired, the quotient can be carried out decimally. To carry the quotient out decimally on an eight column machine, one figure on the right of the divisor will be dropped as each decimal figure is obtained. But in the examples just illustrated this dropping of figures of the divisor will not make any difference in the answer, until the fourth decimal place of the quotient is reached.
Common Fractions.
As in commercial computations common fractions very often occur the most convenient method of multiplying a whole number by a fraction on the Comptometer is given below.
To Multiply a Whole Number by a Fraction. Multiply the whole number by the numerator first. As the product will then be indicated on the register, it can be divided by the denominator; and after pointing off the quotient, the remainder, if any, will constitute a new numerator.
Example: Find the value of 436 multiplied by 4⁄7. After multiplying 436 by 4, 1744 appears on the register. Now divide this amount by 7, and 249 appears as quotient, and 1 as remainder. Ans. 2491⁄7.
To Multiply a Whole Number by a Mixed Number. First multiply by the numerator of the mixed number, and then dividing by the denominator and leaving the result standing on the register, consider the units column of the quotient as the units column on the machine, and multiply by the integral part of the mixed number.
Thus: what is the product of 453 multiplied by 3725⁄16? After multiplying by the numerator, 5, 2265 appears, which being divided by 16, the denominator, 1419⁄16, is the result. As there are two places in the denominator, we ignore the first two columns of the machine and consider the third column as the units or first column, and multiplying by 372, the result, 168,6579⁄16, appears on the register.
Multiplication—Stone Measure.
To multiply feet and inches by feet and inches stone measure, without reducing either of the factors to inches. Multiply the feet of each factor by the inches of the other, leaving the products to accumulate on the register. Multiply mentally the inches of one factor by the inches of the other factor, divide by twelve and strike the result on the machine as in addition. Divide the amount now on the register by twelve, leaving the quotient and the remainder on the register; multiply the feet of one factor by the feet of the other factor, over the quotient, when the number of inches will be indicated in the first two columns on the right of the register and the feet in the columns to the left.
It is obvious that in the mental calculation of the inches by inches, there will sometimes be a slight remainder which will be lost. This can be avoided by calculating it on the machine, instead of mentally, before multiplying feet by inches, and carrying all the operations three places further to the left.
Example: 37 ft. 5 in. multiplied by 19 ft. 11 in.
Multiplying 19 by 5, 95 appears. Then multiplying 11 by 37, 502 appears. 5×11÷12,=4.6. Therefore, add 4, when 506 appears. Dividing this by 12, 42.02 appears. Multiplying 37 by 19 over the quotient, 745 sq. feet. 2 sq. in., stone measure, appears on the register as the answer.
If there are three factors containing feet and inches to be multiplied together to obtain cubic feet and inches, observe in which one the inches can be the most easily stated decimally, then multiply the other factors together as illustrated above, and then multiply the other by the product, by means of one of the methods given for multiplying where the multiplier stands on the register. Page 9. British Exchange.
Adding Pounds, Shillings and Pence.
To add English money on the Comptometer, the pence are added first, and when the bottom of the column is reached, a few strokes on the keys divides it by 12 and places the number of shillings thus found in the next higher column of the register, so that adding the columns of shillings up it will be included in the shillings, while the remainder of the pence will stand to the right. Then after adding up the shillings column and dividing the sum thus obtained by 20, the pounds are added up and the entire sum total in pounds, shillings and pence is indicated on the register.
As each division is made the machine throws the quotient into the proper column, where it is included in the footing of the denomination to which it belongs. As compared to the mind, it saves even more time in adding pounds, shillings and pence than in adding ordinary numbers expressed by the decimal system.
RULE.—First add the pence on the two right hand columns of the machine and divide by 12. The quotient is shillings and the remainder pence. Leave this standing on the register; add up the shillings on the third and fourth columns of the machine. Divide the footing of the shillings by 20 (in doing which you do not touch the three right hand columns of keys). Then add the pounds on the fourth and higher columns of the machine, and the sum total in pounds, shillings and pence is indicated on the register: pence in the first and second columns of the register, shillings in the third and fourth columns of the register, and pounds in the fifth and higher columns of the register.
Example:
| £ | s. | p. |
| 178 | 13 | 3 |
| 526 | 9 | 7 |
| 3476 | 6 | 11 |
| 216 | 3 | 2 |
| 1276 | 16 | 4 |
| 316 | 19 | 11 |
| 124 | 17 | 3 |
Adding up the pence, we have 41. Placing our fingers on the keys (red 11) to divide by 12, we find, after three strokes, that there are 3s and 5d. Leaving this stand on the register and adding up the shillings on the fourth and fifth columns, the register indicates 86s 5d.
Now divide the 86s by 20 (red 1 in the fourth column is the only key used in this case). Four strokes performs the division, when the register indicates £4 6s 5d. Then adding the pounds on the fifth and higher columns the answer, £6116 6s 5d, is shown by the register.
To reduce pounds, shillings and pence to United States Currency, at any given rate, multiply the pounds by 480. Leaving that on the register, multiply the shillings by 24 and the pence by 2; then multiply (by rule for high decimals on page 10) the result, by the number opposite the given rate of exchange in the table, page 27. Point off from the left of the machine two more holes than there are pounds in the bill of exchange, and the answer, expressed in dollars, cents and mills, is shown in the register.
Example: Find the value in dollars of £352 9s 7d at 4.877⁄8.
After multiplying 352 by 480, and on top of that 9s by 24 and 7d by 2, 169190 appears on the register.
The number opposite the rate of exchange (4.877⁄8) being 10164062, multiply 169190 by 10164062 from the left according to the rule for high decimals (page 10), and pointing off five holes from the left of the machine, 1719.656, the answer in dollars, cents and mills, appears on the register.
To reduce dollars and cents to English Currency at any given rate set the dollars and cents so that units of cents will come three columns from the right of the machine and turn down the third pointer and divide by the number in the table, opposite the given rate, until you have obtained the quotient figure one place to the right of the pointer. Subtract out the remainder. If the figure to the right of the pointer be less than five, subtract it out with the remainder; if more than 5, carry one to the left before subtracting it out.
Divide the quotient now standing in the register by 24, then turn down the fifth pointer from the right of the machine and divide the amount to the right of the fifth pointer by 2, and then divide the amount to the left of the fifth pointer by 20; turn down the seventh pointer and that to the left of the seventh pointer is pounds, that between the seventh and fifth pointers is shillings, that in the first column to the right of the fifth pointer is pence, and the figures to the left of that, half pence.
Note: If the remainder after dividing by 24 is over 19, you have to take the remainder off to divide it by 2. Of
course this seldom occurs. In dividing by 20 do not forget that you are through when you have obtained the quotient figure in the seventh column of the machine.
A ten column machine is required to reduce from United States to English money, at one operation, bills of $500.00 and over; but by setting the amount in dollars and cents on the extreme left of the machine, and after dividing by the proper table number, turning to naught and setting the quotient over to the extreme right of the machine, bills of $50,000.00 and over, can be rapidly computed on an eight column machine.
Example: What is the value in English money of $351.24 rate 4.865⁄8.
Setting 351.24 in the register so that 4 will come in the third place from the right; turning down the pointer to the left of the 4 and dividing by 10138021, (10138021 in the table, page 27, opposite 4.865⁄8) until we obtain all the quotient figures to one place to the right of the pointer we have 34645 to the left of the pointer and 6 in the next place to the right of the pointer; as 6 is more than 5, carry one, which makes it 34646 to the left of the third pointer.
Now dividing 34646 by 24 we have 1443+14.
Turning down the fifth pointer and dividing 14 by 2 we have 7. Leave it standing on the register and dividing 1443 by 20 and turning down the seventh pointer we have £72, 3s and 7d.
Table for British Exchange.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Interest.
To perform interest on the Comptometer, the following methods are so rapid that the most complex examples in interest can be computed in twenty-five seconds, and an ordinary example in ten seconds.
No one can compute interest one-half as rapid mentally or by using an interest table.
Method of Computing Interest. If the number of days for the whole term is not known, first strike the number of days on the machine, as in addition; then strike the 30 key as many times as there are months, and the 300 key and the 60 key as many times as there are years. The number of days will then be indicated on the register.
Multiply the principal by the number of days, without taking the number of days off of the register, as illustrated on page 9, and divide the product
- By 90, if the rate is 4%;
- By 72, if the rate is 5%;
- By 60, if the rate is 6%;
- By 45, if the rate is 8%;
- By 40, if the rate is 9%;
and point off four places, if there are no cents in the principal; but if there be cents in the principal, point off six places.
Example: Find the interest on $462 for three years, 7 months and 11 days at 8 per cent. First strike 11, as there are 11 days, then strike the 30 seven times, as there are seven months; and strike the 300 three times, and the 60 three times, as there are three years. 1301 is now indicated. on the register. Multiplying the principal by 1301 and 601062 is given as the product; dividing this by 45, and there is a quotient of 1335642⁄45%; point off four places, and $133.56 appears as the answer.
Where the rate per cent is 7, after multiplying the principal by the number of days, multiply this product by striking each 6 key as many times as the corresponding figure of the register indicates. (See rule page 9.) Then divide the amount now indicated on the register by 36, and if there be no cents in the principal, point off five places; but if there be cents in the principal, point off seven places.
Example: What is the interest of $273 for 6 months and 26 days, at 7 per cent? Computing the number of days, 206 is the answer; and multiplying 273 by 206, 56238 appears on the register. As the rate of interest is 7 per cent, multiply by 7 by using the row of 6s as above directed, and 393666 appears on the register. Dividing by 36 causes 109356⁄36 to appear, and pointing off five places, the answer, $10.935, is obtained.
Discount.
Method of Discounting Bills. Multiply the amount of the bill by the negative of the rate of discount. The product will be the net amount of the bill.
Thus: $524.25, 30 per cent off. To strike the negative of 30 we strike the red 2, (see page 11). Therefore, we begin on the second key from the right on the row of red 2's, and strike each red 2 in succession toward the left, as many times as the corresponding figure in the multiplicand indicates. Thus, striking the red 2 in the second column five times, the next red 2 to the left two times, the next four times, the next two times, and the next five times; and pointing off four places, $366.975 appears as the amount of the bill, after discounting.
It is obvious that to find the discount, all that is necessary is to multiply the principal by the rate of discount.
For discounting bills like the following:
| 24 | 1⁄2 in M.I. Caps | 09 | $2.16 | 22% off. |
| 36 | 1 in. M.I. Ells. | 22 | 7.92 | 30% off. |
| 24 | 1 in. M.I. Tees | 28 | 6.72 | 15% off. |
Multiply the first item negatively by its per cent. off, and leaving the amount standing on the register, proceed to multiply the other items negatively by their per cent. off. The sum of all the items with their discounts deducted will then be indicated on the register.
Thus: After multiplying $2.16 by 22 negatively, $1.6848 appears on the register, and leaving this amount on the register, and multiplying $7.92 by 30 negatively we have $7.2288, and after multiplying $6.72 by 15 negatively, $12.94 appears as the answer.
Where there are several Discounts on one Bill.
Example: $452 less 70%, 47% and 10%.
After multiplying 452 by the red 6 (one less than the 7 of the 70%) we have 135.60. Multiply this by 47 on the red figures (not one less than 47 because 135.60 is already on the machine) we have 71.868, and in the same manner multiply this by red 1 (for the 10%) we have 64.68, the value of the bill after taking off 70%, 47% and 10%.
In multiplying by the red 47 and red 1 use the rule on page 9.
In taking off any per cent. less than 10, remember that such per cent. stated decimally has a cipher before it. Thus, 6% is .06, so for 6% multiply on the row of red naughts for the naught and on the red 5 for the 6.
Compound Interest.
To Perform Compound Interest. Multiply the principal in cents by the rate of interest and add the principal. Set the amount down on paper in dollars and cents, leaving off the mills and tens of mills, and begin on the unit key of the row of keys representing the rate per cent., and without turning the machine to naught, multiply the amount set down by the rate per cent., thereby placing the product two places to the right of the amount standing on the machine. Set down on paper the amout now on the machine, which is the amount of compound interest and principal for two years. Proceed in like manner, as many times as there are years remaining in the term for which the interest is to be compounded.
Example: What is the amount of $326.21 for five years at 7 per cent. compound interest?
Starting on the row of 7's indicated by the rate per cent., strike the first one, one time, the next two times, the third six times, and so on. $22.8347 appears on the register, as the interest for one year. Add the principal and $349.04 appears as the amount of interest and principal for one year, the mills and tenths of mills being disregarded. Starting on the row of 7's, strike the first 7 four times, the third nine times, the fourth four times, and the fifth three times. The amount of interest and principal will now be indicated on the register. Setting this down, continue the operation as directed by above rule, three times more, when the amount of compound interest and principal for five years will be indicated on the register.
Square Root.
Before trying to extract square root, practice division on at least fifty examples, employing those having one, two, and also five figures in the divisor.
The simplest way to extract square root on the Comptometer is to act on the principle that in the series of odd numbers, 1, 3, 5, 7, 9, etc., the square of the number of terms always equals the sum of all the terms.
Thus: In the series 1, 3, 5, 7, 9, 11, 13, we have seven terms, and find that the sum of these terms is 49, and that the square of seven, the number of terms, is also 49.
Method where the first period on the left is not greater than 25. Strike on the keys the number to be operated on, so that it will appear on the register of the machine, and separate it by the pointers above the register into periods of two figures each from the right.
To obtain the first root figure, strike the red 0 key in the units column of the highest period, and each succeeding key towards the register in that column which has a bent top. until the figure in the tens column of that period indicates the number of key strokes, and the figures in the units column indicate an amount not greater than the red figure on the next key to be struck. (This simply amounts to dividing by the series of number of which 1 is the starting point and 2 the common difference.) The figure which now stands in the highest column of the register (the column which was the tens of the first period) is the first root figure, and the figure in the next column to the right is the remainder of the first period.
To obtain the second root figure. To the remainder of the first period annex the next period on the right for a new number from which to obtain the second quotient figure. Multiply the root figure already obtained by 20. If this amount is less than the number composed of the remainder and the next period, use it as a starting point at which to begin striking the series of even numbers according to the red figures, and strike it and each succeeding even number (example, 4×20=80-82-84-86-88, etc.) until the number of even numbers struck coincide with the figure on the register in the column next higher than the highest key struck, and the figures in the column in which the keys are struck indicates an amount not greater than the next even number to be struck. If the first root figure multiplied by 20 is as large or larger than the minuend, the second root figure is 0; therefore annex one more period to the remainder and proceed to find the third root figure.
To find the third and all succeeding root figures. Proceed same as with the second, except that there are two or more root figures to be multiplied by 20.
Two figures can be used as a trial divisor to find each root figure the same as in the method of dividing by three or more numbers, after which strike each of the keys which represent the rest of the even numbers to be struck, the number of times required as indicated by the quotient figure obtained by the trial divisor.
Example: . After striking 14334027 on the machine and pointing off, we find that 14 is the highest period. Striking the red 0 in the units column of that period, then each succeeding key having a crooked top, we find that the figure in the tens column of that period on the register does not coincide with the number of keys struck until three keys are struck, then as 5, which stands in the units column of the period on the register is not greater than the red figure on the next crooked topped key, we have obtained the first root figure. Annexing the next period to the remainder of the first period, we have 533 as a new number from which to obtain the second root figure. The first root figure multiplied by 20=60, therefore place the index finger of the left hand on the red 6, and the index finger of the right hand on the red 0 of the tens and units column of the 533, and strike once; move the right hand finger to the red 2 of its column, strike 62; then to the 4 (all the time watching the figure in the next higher column on the register, and counting the numbers struck), strike 61, and then to the 6, strike 66; then to the 8, strike 68, then move the right hand index finger back to the red 0, at the same time moving the left hand finger to the red 7, strike 70, then moving the right hand to the red 2, strike 72. Now having struck seven even numbers, to coincide with the seven standing on the register in the next higher column than the one on which the keys were struck, we observe the remainder which is 64, and as 64 is not greater than 74, the next even number, the second root figure has been obtained.
Annexing another period to the remainder 64, we have 6440 as a number from which to obtain the third root figure. Multiplying the first two root figures (37) by 20, we have 740 as a starting point from which to begin striking the series of even numbers; use 74 as a trial divisor, and begin striking it on the tens and hundreds column of the number 6440, to find the next root figure. After striking the trial divisor five times, move the right hand finger one key towards the register, as it is apparent that the sixth succeeding even number is always ten greater than the one used as a starting point. We find that not until the trial divisor has been struck 8 times, does the number of strokes coincide with the figure in the next higher column on the register, when the remainder being smaller than the trial divisor, 8 is the third root figure; therefore, we strike the red 0 in the units column of the 6440, and each succeeding bent top key towards the register, and coming to the last one, begin again on the same red 0 key and strike it and the next two succeeding bent keys, making 8 strokes in all, because 8 is the root figure found by using the trial divisor. 456 now appears as the remainder. Annexing the next period we have 45627 as a number from which to obtain the fourth root figure. 378, the root figures already obtained, multiplied by 20 equals 7560. Taking 75 as a trial divisor, we strike 6 times before the number of strokes coincide with the next higher figure (do not drop the right hand finger one key towards the register after the fifth stroke, as when obtaining the third root figure, because 10 added to 7560 would not change either of the figures of the trial divisor), then place the finger on the red 6 in the next column to the right, because 6 is the next figure to the trial divisor, and strike 6 times, because 6 is the root figure obtained by using the trial divisor (drop one key towards the register after the fifth stroke), then strike 6 times in rotation on the series of bent keys of the units column in the usual manner, when the root, 3786, will appear, with the remainder, 231, standing to the right.
Method where the first period on the left is greater than 25. To obtain the first root figure, strike the red 00 in the tens and units columns of the highest period, and then 02, 04, 06, 08, 10, 12, etc., until the number of strokes coincide with the figure in the next higher column on the register, and the remainder standing in the column in which the keys are struck is not greater than the amount represented by the red figure on the keys to be struck.
To obtain the second and all succeeding root figures, proceed the same as for the third root figure illustrated in the method and example given above.
Equations.
There are many equations in which one of the operations is to subtract the product of two numbers or to subtract the square of a number. The following will show how it can be done without finding what the product of the number is or what the square of the number is and thereby saving much time. We have not space in which to illustrate one of each class of such equations but will illustrate examples in two classes which will suffice to give the principle of doing it.
Example 1. (2742 × 58)—(864×74). After multiplying 2742 by 58, 159036 appears as a product. Leave it on the register and deduct one from the multiplier, in this case 74, which leaves 73. Place the finger on the key in the units column which has a red 3 and strike it and each succeeding key to the left in the row bearing red 3's as many times as the corresponding figures of the multiplicand, 864, indicate. Then place the finger on the key in the tens column which bears a red 7 and proceed to strike the row of red 7 keys in the same manner according to the figures of the multiplicand. Next annex as many ciphers to the multiplicand as there are places in the multiplier and subtract it from the amount on the register. In this case there are two places in the multiplier; therefore, subtract 86400, when the answer, 95100, appears on the register.
Example 2. The hypothenuse of a triangle is 1278 feet; the base is 473 feet; what is the perpendicular? The equation is . Squaring 1278 we have 1633284. Leaving it on the register, we multiply 473 by 473 according to the red figures. as illustrated in Example 1, and then annex three ciphers to 473, and subtract it, when 1409555 appears on the register. Extracting the square root, we have 1187, +586. If you desire to express the root as a mixed number, all that is necessary is to multiply the root figures already obtained by 2 and add 1. Then place the result under the remainder as a denominator. In this case it would be as follows: 1187×2=2374. 2374+1=2375; therefore the root is 1187 586.2375.
It is evident that the periods of ciphers can be annexed to the remainder and the root carried out decimally if desired.
![]()
This work is in the public domain in the United States because it was published before January 1, 1929.
This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
![]()
Public domainPublic domainfalsefalse



