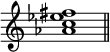of music, and giving a larger scope to the basis of a single key—and thereby avoiding the consideration of innumerable short transitions—he gives a number of chromatic chords as belonging essentially to every key, though their signatures may not be sufficient to supply them, and with the same object builds his fundamental discords on the basis of the supertonic and tonic as well as on the dominant. In respect of this he says—'The reason why the tonic, dominant, and supertonic are chosen for roots, is because the harmonics in nature rise in the same manner; first the harmonics of any given note, then those of its fifth or dominant, then those of the fifth of that dominant, being the second or supertonic of the original note. The reason why the harmonics of the next fifth are not used, is because that note itself is not a note of the diatonic scale, being a little too sharp, as the fifth of the supertonic, and can only be used as part of a chromatic chord.' The advantages of this system of taking a number of chromatic chords under the head of one key will be obvious to any one who wishes for a complete theory to analyse the progressions of keys in modern music as well as their harmonic structure. For instance, even in the early 'Sonata Pathetique' of Beethoven, under a less comprehensive system, it would be held that in the first bar there was a transition from the original key of C minor to G; whereas under this system the first modulation would be held to take place in the 4th bar, to E♭, which is far more logical and systematic.
The detailed examination of the series of chords which have been summarised above is very elaborate. In most cases his views of the resolutions, even of well-known chords, are more varied and comprehensive than is usual with works on harmony, and point to the great patience and care bestowed on the elaboration of the theory. The most salient points of this part of the work are the reduction of well-known chords and their recognised and possible resolutions under the author's system of fundamental discords. The chord of the diminished seventh (a) he points out to be the first inversion of that of the minor ninth (b);

and though this inversion, in which the root is omitted, is decidedly more common than the original chord (b), yet the latter is to be found complete—as is also the major ninth, without omission of the root—in the works of the great masters; and that on tonic and supertonic as well as dominant roots.

The chord of the dominant eleventh, when complete (as c), is hardly likely to be found unabridged;
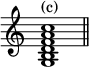
and it is even doubtful whether any examples of its first position exist, even with some notes omitted, which can be pointed to with certainty as an essential chord. But in this scheme the chord is important as giving in its fourth inversion the chord known as the added sixth (d), in which case the fifth of the original chord is at the top and the root and third are omitted, and the free treatment which has generally characterised this formerly isolated chord fully agrees with the rest of the principles of the system.

This chord of the eleventh, unlike the others in the series, can only be used on the dominant, because if used on either the tonic or supertonic it would resolve out of the key. The last chord of the series is that of the major or minor thirteenth on either of the before-mentioned roots; of which the whole chord on the dominant of C (for example) would stand as (e).
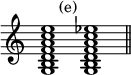
It is not suggested that all these notes occur at once, but that the discordant ones have their own proper resolutions, which they will follow in whatever positions they may be combined; their resolutions being liable to modification by the omission of any notes with which they form dissonances. The commonest and smoothest form of the chord is
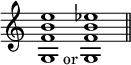
which will be readily recognised; and there are various resolutions given of the interval which makes the thirteenth with the root in this combination. One of the resolutions of the minor thirteenth deserves special consideration, namely, that in which it rises a semitone while the rest of the chord moves to tonic harmony. This makes the chord appear to be the same as that which was and is commonly known as that of the sharp fifth, as (f).

To the whole doctrine of a sharpened fifth Dr. Day strongly opposed himself, and maintained that the two chords marked (g) and (h) in the example were identical; and brought to bear

both mathematics and practical experiment to prove it. The combinations and resolutions which result from his views of the nature of this chord are some of them very curious and original, and would probably be impossible if the chord were not a minor thirteenth but a sharp fifth. Still, the case against the sharp fifth cannot be said to be thoroughly substantiated, and the singular results of his views in this special case are not to be found in great numbers in the works of composers.
The chord of the augmented sixth he derives from the primary harmonics arising from a primary root, and the secondary harmonics arising from a secondary root. Thus in the following chord in the key of C, the lower note A♭ he