object glass should be equal to twice the height of the mirror from the floor. The telescope being now directed towards the mirror will see in it the reflexion of the scale. If the part of the scale where the plumb-line crosses it appears to coincide with the vertical wire of the telescope, then the line of colliraation of the mirror coincides with the plane through the mark and the optical centre of the object glass. If the vertical wire coincides with any other division of the scale, the angular position of the line of collimation is to be found as follows:—
Let the plane of the paper be horizontal, and let the various points be projected on this plane. Let be the centre of the object glass of the telescope, P the fixed mark, P and the vertical wire of the telescope are conjugate foci with respect to the object glass. Let M be the point where OP cuts the plane of the mirror. Let MN be the normal to the mirror; then OMN = θ is the angle which the line of collimation makes with the fixed plane. Let MS be a line in the plane of OM and MN, such that NMS = OMN, then S will be the part of the scale which will be seen by reflexion to coincide with the vertical wire of the telescope. Now, since
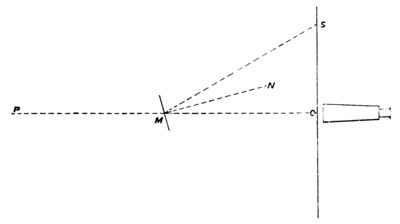
Fig. 14.
MN is horizontal, the projected angles OMN and NMS in the figure are equal, and OMS =2θ. Hence OS = 0M tan 2θ.
We have therefore to measure OM in terms of the divisions of the scale; then, if s0 is the division of the scale which coincides with the plumb-line, and s the observed division,
whence θ may be found. In measuring OM we must remember that if the mirror is of glass, silvered at the back, the virtual image of the reflecting surface is at a distance behind the front surface


