(η). II. 13.
A Pair of Lines, of which one has two points on the same side of, and equidistant from, the other, are eqiddistantial from each other.
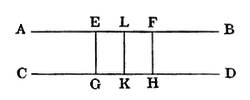
Let AB contain two points E, F, equidistant from CD. From E, F, draw EG, FH, ⊥ CD; bisect GH in K, and EF in L, and join KL.
Now EG = FH; [hyp.
hence, if the diagram be reversed, and so placed on its former traces that G coincides with H, and H with G, K retaining its position, GE coincides with HF, and HF with GE;
∴ E coincides with F, and F with E;
∴ L retains its position;
∴, if there be a point in LA whose distance is < LK, there is another such point in LB, and the Line AB will first recede from and then approach CD; which is absurd. [(ζ).
Similarly if there be one whose distance is > LK.
∴ AB is equidistantial from CD.
Similarly it may be proved that CD is equidistantial from AB.
Therefore a Pair of Lines, &c. Q. E. D.
Lemma 2.
Through a given point may he drawn a common perpendicular to a given Pair of Lines, of which each is equidistantial from the other.

