(·001)2, we can obtain three more figures approximately by dividing 2−(1·414)2 by 2·818.
114. Binomial Theorem.—More generally, if we have obtained a as an approximate value for the pth root of N, the binomial theorem gives as an approximate formula p√N = a + θ, where N = ap + pap−1θ.
115. Series.—A number can often be expressed by a series of terms, such that by taking successive terms we obtain successively closer approximations. A decimal is of course a series of this kind, e.g. 3·14159 . . . means 3 + 1/10 + 4/102 + 1/103 + 5/104 + 9/105 + . . . A series of aliquot parts is another kind, e.g. 3·1416 is a little less than 3+17−1800.
Recurring Decimals are a particular kind of series, which arise from the expression of a fraction as a decimal. If the denominator of the fraction, when it is in its lowest terms, contains any other prime factors than 2 and 5, it cannot be expressed exactly as a decimal; but after a certain point a definite series of figures will constantly recur. The interest of these series is, however, mainly theoretical.
116. Continued Products.—Instead of being expressed as the sum of a series of terms, a number may be expressed as the product of a series of factors, which become successively more and more nearly equal to 1. For example,
3·1416＝3×1047210000＝3 × 13091250＝3 × 2221 × 24992500＝3(1 + 121)(1−12500).
Hence, to multiply by 3·1416, we can multiply by 317, and subtract 12500 (= ·0004) of the result; or, to divide by 3·1416, we can divide by 3, then subtract 122 of the result, and then add 12499 of the new result.
117. Continued Fractions.—The theory of continued fractions (q.v.) gives a method of expressing a number, in certain cases, as a continued product. A continued fraction, of the kind we are considering, is an expression of the form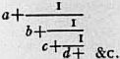 
where b, c, d, . . . are integers, and a is an integer or zero. The expression is usually written, for compactness, a + 1b+ 1c+ 1d+ &c. The numbers a, b, c, d, . . . are called the quotients.
Any exact fraction can be expressed as a continued fraction, and there are methods for expressing as continued fractions certain other numbers, e.g. square roots, whose values cannot be expressed exactly as fractions.
The successive values, a1, ab + 1b, . . ., obtained by taking account of the successive quotients, are called convergents, i.e. convergents to the true value. The following are the main properties of the convergents.
(i) If we precede the series of convergents by 01 and , then the numerator (or denominator) of each term of the series 01, 10, a1, ab+1b . . ., after the first two, is found by multiplying the numerator (or denominator) of the last preceding term by the corresponding quotient and adding the numerator (or denominator) of the term before that. If a is zero, we may regard 1b as the first convergent, and precede the series by 10 and 11.
(ii) Each convergent is a fraction in its lowest terms.
(iii) The convergents are alternately less and greater than the true value.
(iv) Each convergent is nearer to the true value than any other fraction whose denominator is less than that of the convergent.
(v) The difference of two successive convergents is the reciprocal of the product of their denominators; e.g. ab + 1b − a1 = 11·b, and abc + c + abc + 1−ab + 1b = −1b(bc + 1).
It follows from these last three properties that if the successive convergents are p11, p2q2, p3q3, . . . the number can be expressed in the form p1(1 + 1p1q2) (1 − 1p2q3 (1 + 1p3q4) . . . , and that if we go up to the factor 1 ± 1pnqn + 1 the product of these factors differs from the true value of the number by less than ±1qnqn + 1.
In certain cases two or more factors can be combined so as to produce an expression of the form 1 ± 1k, where k is an integer. For instance, 3·1415927 = 3(1 + 13·7) (1 − 122·106) (1 + 1333·113) ...; but the last two of these factors may be combined as (1 − 122·113). Hence 3·1415927 = 31·2221·24852486 . . .
XII. Applications
(i.) Systems of Measures.[1]
118. Metric System.—The metric system was adopted in France at the end of the 18th century. The system is decimal throughout. The principal units of length, weight and volume are the metre, gramme (or gram) and litre. Other units are derived from these by multiplication or division by powers of 10, the names being denoted by prefixes. The prefixes for multiplication by 10, 102, 103 and 104 are deca-, hecto-, kilo- and myria-, and those for division by 10, 102 and 103 are deci-, centi- and milli-; the former being derived from Greek, and the latter from Latin. Thus kilogramme means 1000 grammes, and centimetre means 1100 of a metre. There are also certain special units, such as the hectare, which is equal to a square hectometre, and the micron, which is 11000 of a millimetre.
The metre and the gramme are defined by standard measures preserved at Paris. The litre is equal to a cubic decimetre. The gramme was intended to be equal to the weight of a cubic centimetre of pure water at a certain temperature, but the equality is only approximate.
The metric system is now in use in the greater part of the civilized world, but some of the measures retain the names of old disused measures. In Germany, for instance, the Pfund is 12 kilogramme, and is approximately equal to 1110 ℔ English.
119. British Systems.—The British systems have various origins, and are still subject to variations caused by local usage or by the usage of particular businesses. The following tables are given as illustrations of the arrangement adopted elsewhere in this article; the entries in any column denote multiples or submultiples of the unit stated at the head of the column, and the entries in any row give the expression of one unit in term of the other units.
| Inch. | Foot. | Yard. | Chain. | Furlong. | Mile. |
| 1 | 112 | 136 | 1792 | 17920 | 163360 |
| 12 | 1 | 13 | 166 | 1660 | 15280 |
| 36 | 3 | 1 | 122 | 1220 | 11760 |
| 792 | 66 | 22 | 1 | 10 | 180 |
| 7920 | 660 | 220 | 10 | 1 | 18 |
| 63360 | 5280 | 1760 | 80 | 8 | 1 |
| Ounce. | Pound. | Stone. | Quarter. | Hundred- weight. |
Ton. |
| 1 | 116 | 1224 | 1448 | 11792 | 133840 |
| 16 | 1 | 114 | 128 | 1112 | 12240 |
| 224 | 14 | 1 | 12 | 18 | 1160 |
| 448 | 28 | 2 | 1 | 14 | 180 |
| 1792 | 112 | 8 | 4 | 1 | 120 |
| 33840 | 2240 | 160 | 80 | 20 | 1 |
(Also 7000 grains＝1 ℔ avoirdupois.)
120. Change of System.—It is sometimes necessary, when a quantity is expressed in one system, to express it in another,
- ↑ See also Weights and Measures.
