To compare this with the previous table, φ = (A+B)/A = 1+ρ. Except when the limiting stresses are of opposite sign, the two tables agree very well. In bridge work this occurs only in some of the bracing bars.
It is a matter of discussion whether, if fatigue is allowed for by the Weyrauch method, an additional allowance should be made for impact. There was no impact in Wöhler’s experiments, and therefore it would seem rational to add the impact allowance to that for fatigue; but in that case the bridge sections become larger than experience shows to be necessary. Some engineers escape this difficulty by asserting that Wöhler’s results are not applicable to bridge work. They reject the allowance for fatigue (that is, the effect of repetition) and design bridge members for the total dead and live load, plus a large allowance for impact varied according to some purely empirical rule. (See Waddell, De Pontibus, p.7.) Now in applying Wöhler’s law, fmax. for any bridge member is found for the maximum possible live load, a live load which though it may sometimes come on the bridge and must therefore be provided for, is not the usual live load to which the bridge is subjected. Hence the range of stress, fmax.−fmin., from which the working stress is deduced, is not the ordinary range of stress which is repeated a practically infinite number of times, but is a range of stress to which the bridge is subjected only at comparatively long intervals. Hence practically it appears probable that the allowance for fatigue made in either of the tables above is sufficient to cover the ordinary effects of impact also.
English bridge-builders are somewhat hampered in adopting rational limits of working stress by the rules of the Board of Trade. Nor do they all accept the guidance of Wöhler’s law. The following are some examples of limits adopted. For the Dufferin bridge (steel) the working stress was taken at 6.5 tons per sq. in. in bottom booms and diagonals, 6.0 tons in top booms, 5.0 tons in verticals and long compression members. For the Stanley bridge at Brisbane the limits were 6.5 tons per sq. in. in compression boom, 7.0 tons in tension boom, 5.0 tons in vertical struts, 6.5 tons in diagonal ties, 8.0 tons in wind bracing, and 6.5 tons in cross and rail girders. In the new Tay bridge the limit of stress is generally 5 tons per sq. in., but in members in which the stress changes sign 4 tons per sq. in. In the Forth bridge for members in which the stress varied from 0 to a maximum frequently, the limit was 5.0 tons per sq. in., or if the stress varied rarely 5.6 tons per sq. in.; for members subjected to alternations of tension and thrust frequently 3.3 tons per sq. in. or 5 tons per sq. in. if the alternations were infrequent. The shearing area of rivets in tension members was made 11/2 times the useful section of plate in tension. For compression members the shearing area of rivets in butt-joints was made half the useful section of plate in compression.

|
| Fig. 37. |
20. Determination of Stresses in the Members of Bridges.—It is convenient to consider beam girder or truss bridges, and it is the stresses in the main girders which primarily require to be determined. A main girder consists of an upper and lower flange, boom or chord and a vertical web. The loading forces to be considered are vertical, the horizontal forces due to wind pressure are treated separately and provided for by a horizontal system of bracing. For practical purposes it is accurate enough to consider the booms or chords as carrying exclusively the horizontal tension and compression and the web as resisting the whole of the vertical and, in a plate web, the equal horizontal shearing forces. Let fig. 37 represent a beam with any system of loads W1, W2, . . . Wn.
The reaction at the right abutment is
R2 = W1x1/l+W2x2/l+. . .
That at the left abutment is
R1 = W1+W2+ . . .−R2.
Consider any section a b. The total shear at a b is
S = R–Σ(W1+W2 . . .)
where the summation extends to all the loads to the left of the section. Let p1, p2 . . . be the distances of the loads from a b, and p the distance of R1 from a b; then the bending moment at a b is
M = R1p−Σ(W1p1+W2p2 . . .)
where the summation extends to all the loads to the left of a b. If the loads on the right of the section are considered the expressions are similar and give the same results.
If At Ac are the cross sections of the tension and compression flanges or chords, and h the distance between their mass centres, then on the assumption that they resist all the direct horizontal forces the total stress on each flange is
Ht = Hc = M/h
and the intensity of stress of tension or compression is
ft = M/At h,
fc = M/Ach.
If A is the area of the plate web in a vertical section, the intensity of shearing stress is
fx = S/A
and the intensity on horizontal sections is the same. If the web is a braced web, then the vertical component of the stress in the web bars cut by the section must be equal to S.
|
| Fig. 38. |
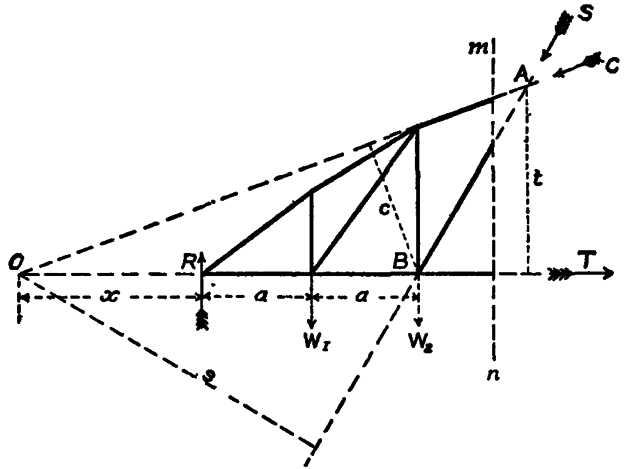
21. Method of Sections. A. Ritter’s Method.—In the case of braced structures the following method is convenient: When a section of a girder can be taken cutting only three bars, the stresses in the bars can be found by taking moments. In fig. 38 m n cuts three bars, and the forces in the three bars cut by the section are C, S and T. There are to the left of the section the external forces, R, W1, W2. Let s be the perpendicular from O, the join of C and T on the direction of S; t the perpendicular from A, the join of C and S on the direction of T; and c the perpendicular from B, the join of S and T on the direction of C. Taking moments about O,
Rx−W1(x+a)−W2(x+2a) = Ss;
taking moments about A,
R3a−W12a−W2a = Tt;
and taking moments about B,
R2a−W1a = Cc
Or generally, if M1 M2 M3 are the moments of the external forces to the left of O, A, and B respectively, and s, t and c the perpendiculars from O, A and B on the directions of the forces cut by the section, then
Ss = M1; Tt = M2 and Cc = M3.
Still more generally if H is the stress on any bar, h the perpendicular distance from the join of the other two bars cut by the section, and M is the moment of the forces on one side of that join,
Hh = M.
 |

|
| Fig. 39. | Fig. 40. |
22. Distribution of Bending Moment and Shearing Force.—Let a girder of span l, fig. 39, supported at the ends, carry a fixed load W at m from the right abutment. The reactions at the abutments are R1 = Wm/l and R2 = W(l−m)/l. The shears on vertical sections to the left and right of the load are R1 and −R2, and the distribution of shearing force is given by two rectangles. Bending moment increases uniformly from either abutment to the load, at which the bending moment is M = R2m = R1(l−m). The distribution of bending moment is given by the ordinates of a triangle. Next let the girder carry a uniform load w per ft. run (fig. 40). The total load

