anorthic systems. It was, however, noticed by Brewster himself
that there are many apparent exceptions, and the “optical
anomalies” of crystals have been the subject of much study.
The intimate relations existing between various other physical
properties of crystals and their external form have subsequently
been gradually traced.
The symmetry of crystals, though recognized by Romé de l’Isle and Haüy, in that they replaced all similar edges and corners of their primitive forms by similar secondary planes, was not made use of in defining the six systems of crystallization, which depended solely on the lengths and inclinations of the axes of reference. It was, however, necessary to recognize that in each system there are certain forms which are only partially symmetrical, and these were described as hemihedral and tetartohedral forms (i.e. ἡμι-, half-faced, and τέταρτος, quarter-faced forms).
As a consequence of Haüy’s law of rational intercepts, or, as it is more often called, the law of rational indices, it was proved by J. F. C. Hessel in 1830 that thirty-two types of symmetry are possible in crystals. Hessel’s work remained overlooked for sixty years, but the same important result was independently arrived at by the same method by A. Gadolin in 1867. At the present day, crystals are considered as belonging to one or other of thirty-two classes, corresponding with these thirty-two types of symmetry, and are grouped in six systems. More recently, theories of crystal structure have attracted attention, and have been studied as purely geometrical problems of the homogeneous partitioning of space.
The historical development of the subject is treated more fully in the article Crystallography in the 9th edition of this work. Reference may also be made to C. M. Marx, Geschichte der Crystallkunde (Karlsruhe and Baden, 1825); W. Whewell, History of the Inductive Sciences, vol. iii. (3rd ed., London, 1857); F. von Kobell, Geschichte der Mineralogie von 1650–1860 (München, 1864); L. Fletcher, An Introduction to the Study of Minerals (British Museum Guide-Book); L. Fletcher, Recent Progress in Mineralogy and Crystallography [1832–1894] (Brit. Assoc. Rep., 1894).
The fundamental laws governing the form of crystals are:—
1. Law of the Constancy of Angle.
2. Law of Symmetry.
3. Law of Rational Intercepts or Indices.
According to the first law, the angles between corresponding faces of all crystals of the same chemical substance are always the same and are characteristic of the substance.
(a) Symmetry of Crystals.
Crystals may, or may not, be symmetrical with respect to a point, a line or axis, and a plane; these “elements of symmetry” are spoken of as a centre of symmetry, an axis of symmetry, and a plane of symmetry respectively.
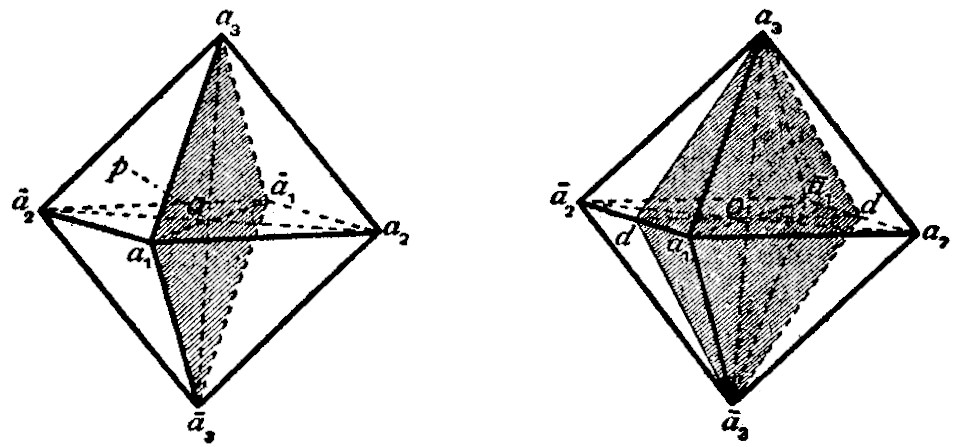
Centre of Symmetry.—Crystals which are centro-symmetrical have their faces arranged in parallel pairs; and the two parallel faces, situated on opposite sides of the centre (O in fig. 3) are alike in surface characters, such as lustre, striations, and figures of corrosion. An octahedron (fig. 3) is bounded by four pairs of parallel faces. Crystals belonging to many of the hemihedral and tetartohedral classes of the six systems of crystallization are devoid of a centre of symmetry.
Axes of Symmetry.—Consider the vertical axis joining the opposite corners a3 and ā3 of an octahedron (fig. 3) and passing through its centre O: by rotating the crystal about this axis through a right angle (90°) it reaches a position such that the orientation of its faces is the same as before the rotation; the face ā1ā2ā3, for example, coming into the position of a1ā2a3. During a complete rotation of 360° (= 90° × 4), the crystal occupies four such interchangeable positions. Such an axis of symmetry is known as a tetrad axis of symmetry. Other tetrad axes of the octahedron are a2ā2 and a1a1.
An axis of symmetry of another kind is that which passing through the centre O is normal to a face of the octahedron. By rotating the crystal about such an axis Op (fig. 3) through an angle of 120° those faces which are not perpendicular to the axis occupy interchangeable positions; for example, the face a1a3a2 comes into the position of ā2a1ā3, and ā2a1ā3 to a3ā2ā1. During a complete rotation of 360° (= 120° × 3) the crystal occupies similar positions three times. This is a triad axis of symmetry; and there being four pairs of parallel faces on an octahedron, there are four triad axes (only one of which is drawn in the figure).
 | |
| Fig. 3. | Fig. 4. |
| Axes and Planes of Symmetry of an Octahedron. | |
An axis passing through the centre O and the middle points d of two opposite edges of the octahedron (fig. 4), i.e. parallel to the edges of the octahedron, is a dyad axis of symmetry. About this axis there may be rotation of 180°, and only twice in a complete revolution of 360° (= 180° × 2) is the crystal brought into interchangeable positions. There being six pairs of parallel edges on an octahedron, there are consequently six dyad axes of symmetry.
A regular octahedron thus possesses thirteen axes of symmetry (of three kinds), and there are the same number in the cube. Fig. 5 shows the three tetrad (or tetragonal) axes (aa), four triad (or trigonal) axes (pp), and six dyad (diad or diagonal) axes (dd).
Although not represented in the cubic system, there is still another kind of axis of symmetry possible in crystals. This is the hexad axis or hexagonal axis, for which the angle of rotation is 60°, or one-sixth of 360°. There can be only one hexad axis of symmetry in any crystal (see figs. 77-80).
 |
| Fig. 5.—Axes of Symmetry of a Cube. |
Planes of Symmetry.—A regular octahedron can be divided into two equal and similar halves by a plane passing through the corners a1a3ā1ā3 and the centre O (fig. 3). One-half is the mirror reflection of the other in this plane, which is called a plane of symmetry. Corresponding planes on either side of a plane of symmetry are inclined to it at equal angles. The octahedron can also be divided by similar planes of symmetry passing through the corners a1a2ā1ā2 and a2a3ā2ā3. These three similar planes of symmetry are called the cubic planes of symmetry, since they are parallel to the faces of the cube (compare figs. 6-8, showing combinations of the octahedron and the cube).
A regular octahedron can also be divided symmetrically into two equal and similar portions by a plane passing through the corners a3 and ā3, the middle points d of the edges a1ā2 and ā1a2, and the centre O (fig. 4). This is called a dodecahedral plane of symmetry, being parallel to the face of the rhombic dodecahedron which truncates the edge a1a2 (compare fig. 14, showing a combination of the octahedron and rhombic dodecahedron). Another similar plane of symmetry is that passing through the corners a3ā3 and the middle points of the edges a1a2 and ā1ā2, and altogether there are six dodecahedral planes of symmetry, two through each of the corners a1, a2, a3 of the octahedron.
