Page:EB1911 - Volume 07.djvu/599

of the first and second orders when the indices are {111} and {101} respectively: ABB is the face (111), and ACC is (101). A combination of these two forms is shown in fig. 45.

Fig. 46.—Ditetragonal
Bipyramid.

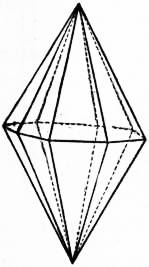
Ditetragonal bipyramid (fig. 46). This is the general form; it is bounded by sixteen scalene triangles, and all the indices are unequal, being {321}, &c., or {hkl}.

Tetragonal prism of the first order. The four faces intersect the horizontal axes in equal lengths and are parallel to the principal axis; the indices are therefore {110}. This form does not enclose space, and is therefore called an “open form” to distinguish it from a “closed form” like the tetragonal bipyramids and all the forms of the cubic system. An open form can exist only in combination with other forms; thus fig. 47 is a combination of the tetragonal prism {110} with the basal pinacoid {001}. If the faces (110) and (001) are of equal size such a figure will be geometrically a cube, since all the angles are right angles; the variety of apophyllite known as tesselite crystallizes in this form.

Tetragonal prism of the second order. This has the same number of faces as the last prism, but differs in position; each face being parallel to the vertical axis and one of the horizontal axes; the indices are {100}.

Ditetragonal prism. This consists of eight faces all parallel to the principal axis and intercepting the horizontal axes in different lengths; the indices are {210}, {320}, &c., or {hko}.

Basal pinacoid (from πίναξ, a tablet). This consists of a single pair of parallel faces perpendicular to the principal axis. It is therefore an open form and can exist only in combination (fig. 47).

Fig. 47. Combination of Tetragonal Prism and Basal Pinacoid.	Fig. 48.	Fig. 49.
Combinations of Tetragonal Prisms and Pyramids.

Combinations of holohedral tetragonal forms are shown in figs. 47–49; fig. 48 is a combination of a bipyramid of the first order with one of the second order and the prism of the first order; fig. 49 a combination of a bipyramid of the first order with a ditetragonal bipyramid and the prism of the second order. Compare also figs. 87 and 88.

Examples of substances which crystallize in this class are cassiterite, rutile, anatase, zircon, thorite, vesuvianite, apophyllite, phosgenite, also boron, tin, mercuric iodide.

Scalenohedral Class

(Bisphenoidal-hemihedral).

Here there are only three dyad axes and two planes of symmetry, the former coinciding with the crystallographic axes and the latter bisecting the angles between the horizontal pair. The dyad axis of symmetry, which in this class coincides with the principal axis of the crystal, has certain of the characters of a tetrad axis, and is sometimes called a tetrad axis of “alternating symmetry”; a face on the upper half of the crystal if rotated through 90° about this axis and reflected across the equatorial plane falls into the position of a face on the lower half of the crystal. This kind of symmetry, with simultaneous rotation about an axis and reflection across a plane, is also called “composite symmetry.”

In this class all except two of the simple forms are geometrically the same as in the holosymmetric class.

Bisphenoid (σφήν, a wedge) (fig. 50). This is a double wedge-shaped solid bounded by four equal isosceles triangles; it has the indices {111}, {211}, {112}, &c., or in general {hhl}. By suppressing either one or other set of alternate faces of the tetragonal bipyramid of the first order (fig. 42) two bisphenoids are derived, in the same way that two tetrahedra are derived from the regular octahedron.

Tetragonal scalenohedron or ditetragonal bisphenoid (fig. 51). This is bounded by eight scalene triangles and has the indices {hkl}. It may be considered as the hemihedral form of the ditetragonal bipyramid.

Fig. 50.—Tetragonal Bisphenoids.	Fig. 51.—Tetragonal Scalenohedron.

The crystal of chalcopyrite (CuFeS₂) represented in fig. 52 is a combination of two bisphenoids (P and P′), two bipyramids of the second order (b and c), and the basal pinacoid (a). Stannite (Cu₂FeSnS₄), acid potassium phosphate (H₂KPO₄), mercuric cyanide, and urea (CO(NH₂)₂) also crystallize in this class.

Bipyramidal Class

(Parallel-faced hemihedral).

The elements of symmetry are a tetrad axis with a plane perpendicular to it, and a centre of symmetry. The simple forms are the same here as in the holosymmetric class, except the prism {hko}, which has only four faces, and the bipyramid {hkl}, which has eight faces and is distinguished as a “tetragonal pyramid of the third order.”

Fig. 52.—Crystal of Chalcopyrite.	Fig. 53.—Crystal of Fergusonite.

Fig. 53 shows a combination of a tetragonal prism of the first order with a tetragonal bipyramid of the third order and the basal pinacoid, and represents a crystal of fergusonite. Scheelite (q.v.), Scapolite (q.v.), and erythrite (C₄H₁₀O₄) also crystallize in this class.

Pyramidal Class

(Hemimorphic-tetartohedral).

Here the only element of symmetry is the tetrad axis. The pyramids of the first {hhl}, second {hol} and third {hkl} orders have each only four faces at one or other end of the crystal, and are hemimorphic. All the simple forms are thus open forms.

Examples are wulfenite (PbMoO₄) and barium antimonyl dextro-tartrate (Ba(SbO)₂(C₄H₄O₆)·H₂O).

Ditetragonal Pyramidal Class

(Hemimorphic-hemihedral).

Here there are two pairs of vertical planes of symmetry intersecting in the tetrad axis. The pyramids {hhl} and {hol} and the bipyramid {hkl} are all hemimorphic.

Examples are iodosuccimide (C₄H₄O₂NI), silver fluoride (AgF·H₂O), and penta-erythrite (C₅H₁₂O₄). No examples are known amongst minerals.

Trapezohedral Class

(Trapezohedral-hemihedral).

Here there are the full number of axes of symmetry, but no planes or centre of symmetry. The general form {hkl} is bounded by eight trapezoidal faces and is the tetragonal trapezohedron.