through tubes of micanite or specially prepared paper lining the slots; or with single-turn loops, stout bars of copper of U-shape can be driven through the slots and closed by soldered connexions at the other end.
The first experimental determination of the shape of the E.M.F. curve of an alternator was made by J. Joubert in 1880. A revolving contact-maker charged a condenser with the E.M.F. produced by the armature at a particular instant during each period. The condenser was discharged through a ballistic galvanometer, and from Shape of E.M.F. curve.the measured throw the instantaneous E.M.F. could be deduced. The contact-maker was then shifted through a small angle, and the instantaneous E.M.F. at the new position corresponding to a different moment in the period was measured; this process was repeated until the E.M.F. curve for a complete period could be traced. Various modifications of the same principle have since been used, and a form of “oscillograph” (q.v.) has been perfected which is well adapted for the purpose of tracing the curves both of E.M.F. and of current. The machine on which Joubert carried out his experiments was a Siemens disk alternator having no iron in its armature, and it was found that the curve of E.M.F. was practically identical with a sine curve. The same law has also been found to hold true for a smooth-core ring or drum armature, but the presence of the iron core enables the armature current to produce greater distorting effect, so that the curves under load may vary considerably from their shape at no load. In toothed armatures, the broken surface of the core, and the still greater reaction from the armature current, may produce wide variations from the sine law, the general tendency being to give the E.M.F. curve a more peaked form. The great convenience of the assumption that the E.M.F. obeys the sine law has led to its being very commonly used as the basis for the mathematical analysis of alternator problems; but any deductions made from this premiss require to be applied with caution if they are likely to be modified by a different shape of the curve. Further, the same alternator will give widely different curves even of E.M.F., and still more so of current, according to the nature of the external circuit to which it is connected. As will be explained later, the phase of the current relatively to the E.M.F. depends not only on the inductance of the alternator itself, but also upon the inductance and capacity of the external circuit, so that the same current will produce different effects according to the amount by which it lags or leads. The question as to the relative advantages of differently shaped E.M.F. curves has led to much discussion, but can only be answered by reference to the nature of the work that the alternator has to do—i.e. whether it be arc lighting, motor driving, or incandescent lighting through transformers. The shape of the E.M.F. curve is, however, of great importance in one respect, since upon it depends the ratio of the maximum instantaneous E.M.F. to the effective value, and the insulation of the entire circuit, both external and internal, must be capable of withstanding the maximum E.M.F. While the maximum value of the sine curve is √2 or 1·414 times the effective value, the maximum value of a Λ curve is 1·732 times the effective value, so that for the same effective E.M.F. the armature wires must not only be more heavily insulated than in the continuous-current dynamo, but also the more peaked the curve the better must be the insulation.
Since an alternating current cannot be used for exciting the field-magnet, recourse must be had to some source of a direct current. This is usually obtained from a small auxiliary continuous-current dynamo, called an exciter, which may be an entirely separate machine, separately driven and used for exciting several alternators, or Excitation.may be driven from the alternator itself; in the latter case the armature of the exciter is often coupled directly to the rotating shaft of the alternator, while its field-magnet is attached to the bed-plate. Although separate excitation is the more usual method, the alternator can also be made self-exciting if a part or the whole of the alternating current is “rectified,” and thus converted into a direct current.
 |
| Fig. 39. |
 |
| Fig. 40. |
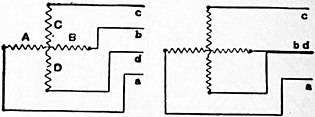
The general idea of the polyphase alternator giving two or more E.M.F.’s of the same frequency, but displaced in phase, has been already described. The several phases may be entirely independent, and such was the case with the early polyphase machines of Gramme, who used four independent circuits, and also in the large Quarter-phase alternators.two-phase alternators designed by J. E. H. Gordon in 1883. If the phases are thus entirely separate, each requires two collector rings and two wires to its external circuit, i.e. four in all for two-phase and six for three-phase machines. The only advantage of the polyphase machine as thus used is that the whole of the surface of the armature core may be efficiently covered with winding, and the output of the alternator for a given size be thereby increased. It is, however, also possible so to interlink the several circuits of the armature that the necessary number of transmitting lines to the external circuits may be reduced, and also the weight of copper in them for a given loss in the transmission.[1] The condition which obviously must be fulfilled, for such interlinking of the phases to be possible, is that in the lines which are to meet at any common junction the algebraic sum of the instantaneous currents, reckoned as positive if away from such junction and as negative if towards it, must be zero. Thus if the phases be diagrammatically represented by the relative angular position of the coils in fig. 39, the current in the coils A and B differs in phase from the current in the coils C and D by a quarter of a period or 90°; hence if the two wires b and d be replaced by the single wire bd, this third wire will serve as a common path for the currents of the two phases either outwards or on their return. At any instant the value of the current in the third wire must be the vector sum of the two currents in the other wires, and if the shape of the curves of instantaneous E.M.F. and current are identical, and are assumed to be sinusoidal, the effective value of the current in the third wire will be the vector sum of the effective values of the currents in the other wires; in other words, if the system is balanced, the effective current in the third wire is √2, or 1·414 times the current in either of the two outer wires. Since the currents of the two phases do not reach their maximum values at the same time, the sectional area of the third wire need not be twice that of the others; in order to secure maximum efficiency by employing the same current density in all three wires, it need only be 40% greater than that of either of the outer wires. The effective voltage between the external leads may in the same way be calculated by a vector diagram, and with the above star connexion the voltage between the outer pair of wires a and c is √2, or 1·414 times the voltage between either of the outer wires and the common wire bd. Next, if the four coils are joined up into a continuous helix, just as in the winding of a continuous-current machine, four wires may be attached to equidistant points at the opposite ends of two diameters at right angles to each other (fig. 40). Such a method is known as the mesh connexion, and gives a perfectly symmetrical four-phase system of distribution. Four collecting rings are necessary if the armature rotates, and there is no saving in copper in the transmitting lines; but the importance of the arrangement lies in its use in connexion with rotary converters, in which it is necessary that the winding of the armature should form a closed circuit. If e=the effective voltage of one phase A, the voltage between any pair of adjacent lines in the diagram is e, and between m and o or n and p is e √2. The current in any line is the resultant of the currents in the two phases connected to it, and its effective value is c √2, where c is the current of one phase.
 |
| Fig. 41. |
- ↑ As in the historical transmission of energy from Lauffen to Frankfort (1891).

