We should then know that there must be equal tangential
traction directed along the length of the bar, and exerted across
some planes or other which are parallel to this direction. We
should also know that, at the bounding surface, these planes
must cut this surface at right angles. The corresponding strain
would be shearing strain which could involve (i.) a sliding
of elements of one cross-section relative to another, (ii.) a relative
sliding of elements of the above mentioned planes in the direction
of the length of the bar. We could conclude that there may
be a longitudinal displacement of the elements of the cross-sections.
We should then attempt to satisfy the conditions
of the problem by supposing that this is the character of the
strain, and that the corresponding displacement consists of
(i.) a rotation of the cross-sections in their planes such as we
found in the case of the circle, (ii.) a distortion of the cross-sections
into curved surfaces by a displacement (w) which is
directed normally to their planes and varies in some manner
from point to point of these planes. We could show that all
the conditions of the problem are satisfied by this assumption,
provided that the longitudinal displacement (w), considered as
a function of the position of a point (x, y) in the cross-section,
satisfies the equation
| ∂2w | + | ∂2w | = 0, |
| ∂x2 | ∂y2 |
and the boundary condition
| ( | ∂w | − τy) cos(x,ν) + ( | ∂w | + τx) cos(y,ν) = 0, |
| ∂x | ∂y |
where τ denotes the amount of the twist, and ν the direction
of the normal to the boundary. The solution is known for a
great many forms of section. (In the particular case of a circular
section w vanishes.) The tangential traction at any point of
the cross-section is directed along the tangent to that curve
of the family ψ = const. which passes through the point, ψ being
the function determined by the equations
| ∂w | = τ ( | ∂ψ | + y ), | ∂w | = − τ ( | ∂ψ | + x ). |
| ∂x | ∂y | ∂y | ∂x |
The amount of the twist τ produced by terminal couples of magnitude G is G/C, where C is a constant, called the “torsional rigidity” of the prism, and expressed by the formula
| C = μ ( | ∂ψ | ) | 2 | + ( | ∂ψ | ) | 2 | dxdy, |
| ∂x | ∂y |
the integration being taken over the cross-section. When the coefficient of μ in the expression for C is known for any section, μ can be determined by experiment with a bar of that form of section.
 |  |
| Fig. 4. | Fig. 5. |
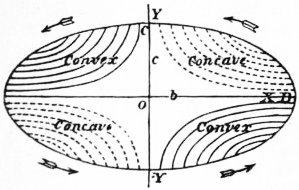
43. The distortion of the cross-sections into curved surfaces is shown graphically by drawing the contour lines (w = const.). In general the section is divided into a number of compartments, and the portions that lie within two adjacent compartments are respectively concave and convex. This result is illustrated in the accompanying figures (fig. 4 for the ellipse, given by x2/b2 + y2/c2 = 1; fig. 5 for the equilateral triangle, given by (x + 13a) (x2 − 3y2 − 43ax + 49a2) = 0; fig. 6 for the square).
44. The distribution of the shearing stress over the cross-section is determined by the function ψ, already introduced. If we draw the curves ψ = const., corresponding to any form of section, for equidifferent values of the constant, the tangential traction at any point on the cross-section is directed along the tangent to that curve of the family which passes through the point, and the magnitude of it is inversely proportional to the distance between consecutive curves of the family. Fig. 7 illustrates the result in the case of the equilateral triangle. The boundary is, of course, one of the lines. The “lines of shearing stress” which can thus be drawn are in every case identical with the lines of flow of frictionless liquid filling a cylindrical vessel of the same cross-section as the bar, when the liquid circulates in the plane of the section with uniform spin. They are also the same as the contour lines of a flexible and slightly extensible membrane, of which the edge has the same form as the bounding curve of the cross-section of the bar, when the membrane is fixed at the edge and slightly deformed by uniform pressure.
 |
| Fig. 6. |
 |
| Fig. 7. |
45. Saint-Venant’s theory shows that the true torsional rigidity is in general less than that which would be obtained by extending Coulomb’s law (G = μτI) to sections which are not circular. For an elliptic cylinder of sectional area ω and moment of inertia I about its central-line the torsional rigidity is μω4 / 4π2I, and this formula is not far from being correct for a very large number of sections. For a bar of square section of side a centimetres, the torsional rigidity in C.G.S. units is (0.1406) μa4 approximately, μ being expressed in dynes per square centimetre. How great the defect of the true value from that given by extending Coulomb’s law may be in the case of sections with projecting corners is shown by the diagrams (fig. 8 especially no. 4). In these diagrams the upper of the two numbers under each figure indicates the fraction which the true torsional rigidity corresponding to the section is of that value which would be obtained by extending Coulomb’s law; and the lower of the two numbers indicates the ratio which the torsional rigidity for a bar of the corresponding section bears to that of a bar of circular section of the same material and of equal sectional area. These results have an important practical application, inasmuch as they show that strengthening ribs and projections, such as are introduced in engineering to give stiffness to beams, have the reverse of a good effect when torsional stiffness is an object, although they are of great value in increasing the resistance to bending. The theory shows further that the resistance to torsion is very seriously diminished when there is in the surface any dent approaching to a re-entrant angle. At such a place the shearing strain tends to become infinite, and some


