consider carefully fig. 21, which shows that, when the root is a prime,
and not composite, number, as 7, eight letters a, b, . . . h may proceed
from any, the same, cell, suppose that marked 0, each letter being
repeated in the cells along different paths. These eight paths are
called “normal paths,” their number being one more than the root.
Observe here that, excepting the cells from which any two letters
start, they do not occupy again the
Fig. 21
same cell, and that two letters, starting
from any two different cells along different
paths, will appear together in one
and only one cell. Hence, if p1 be placed
in the cells of one of the n + 1 normal
paths, each of the remaining n normal
paths will contain one, and only one,
of these p1’s. If now we fill each row
with p2, p3, . . . pn in the same order,
commencing from the p1 in that row,
the p2’s, p3’s and pn’s will lie each in a
path similar to that of p1, and each of
the n normal paths will contain one,
and only one, of the letters p1, p2,. . . pn,
whose sum will be Σp. Similarly, if
q1 be placed along any of the normal paths, different from that of
the p’s, and each row filled as above with the letters q2, q3, . . . qn,
the sum of the q’s along any normal path different from that of
the q1 will be Σq. The n2 cells of the square will now be found to
contain all the combinations of the p’s and q’s; and if the q’s
be multiplied by n, the p’s made equal to 1, 2, . . . n, and the q’s
to 0, 1, 2, . . . (n − 1) in any order, the Nasik square of n will be
obtained, and the summations along all the normal paths, except
those traversed by the p’s and q’s, will be the constant Σnq + Σp.
When the root is an odd composite number, as 9, 15, &c., it will be
found that in some paths, different from the two along which the
p1 and q1 were placed, instead of having each of the p’s and q’s,
some will be wanting, while some are repeated. Thus, in the case
of 9, the triplets, p1p4p7, p2p5p8, p3p6p9, and q1q4q7, q2q5q8, q3q6q9 occur,
each triplet thrice, along paths whose summation should be—Σp 45
and Σr 36. But if we make p1, p2, . . . p9, = 1, 3, 6, 5, 4, 7, 9, 8, 2, and
the r1, r2, . . . r9 = 0, 2, 5, 4, 3, 6, 8, 7, 1, thrice each of the above sets
of triplets will equal Σp and
Σq respectively. If now the
q’s are multiplied by 9, and
added to the p’s in their
several cells, we shall have a
Nasik square, with a constant
summation along eight of its
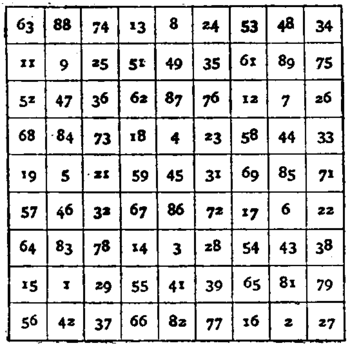
ten normal paths. In fig. 22
the numbers are in the nonary
scale; that in the centre is
the middle one of 1 to 92, and
the sum of pair of numbers
equidistant from and opposite
to the central 45 is twice 45;
and the sum of any number
and the 8 numbers 3 from it,
diagonally, and in its row and
column, is the constant Nasical
summation, e.g. 72 and
32, 22, 76, 77, 26, 37, 36, 27. The numbers in fig. 22 being kept
in the nonary scale, it is not necessary to add any nine of them
together in order to test the Nasical summation; for, taking the
first column, the figures in the place of units are seen at once
to form the series, 1, 2, 3, . . . 9, and those in the other place three
triplets of 6, 1, 5. For the squares of 15 the p’s and q’s may be
respectively 1, 2, 10, 8, 6, 14, 15, 11, 4, 13, 9, 7, 3, 12, 5, and 0, 1, 9, 7,
5, 13, 14, 10, 3, 12, 8, 6, 2, 11, 4, where five times the sum of every
third number and three times the sum of every fifth number makes
Σp and Σq; then, if the q’s are multiplied by 15, and added to the
p’s, the Nasik square of 15
is obtained. When the root
is the multiple of 4, the same
process gives us, for the
square of 4, fig. 23. Here
the columns give Σp, but
alternately 2q1, 2q3, and 2q2,
2q4; and the rows give Σq,
but alternately 2p1, 2p3,
and 2p2, 2p4; the diagonals
giving Σp and Σq. If p1, p2, p3, p4 and q1, q2, q3, q4 be 1, 2, 4, 3,
and 0, 1, 3, 2, we have the Nasik square of fig. 24. A square like this
is engraved in the Sanskrit character on the gate of the fort of
Gwalior, in India. The squares of higher multiples of 4 are readily
obtained by a similar adjustment.
 |
| Fig. 22. |
 |  |
| Fig. 23. | Fig. 24. |
Nasik Cubes.—A Nasik cube is composed of n3 small equal cubes,
here called cubelets, in the centres of which the natural numbers
from 1 to n3 are so placed that every section of the cube by planes
Fig. 25—Nasik Cube.
perpendicular to an edge has the properties of a Nasik square; also
sections by planes perpendicular to a face, and passing through the
cubelet centres of any path of Nasical summation in that face.
Fig. 25 shows by dots the way in which these cubes are constructed.
A dot is here placed on three faces of a cubelet at the corner, showing
that this cubelet belongs to each of the faces AOB, BOC, COA, of
the cube. Dots are placed on the cubelets of some path of AOB
(here the knight’s path), beginning from O, also on the cubelets of
a knight’s path in BOC. Dots are now placed in the cubelets of
similar paths to that on BOC in the other six sections parallel to
BOC, starting from their dots in AOB. Forty-nine of the three
hundred and forty-three cubelets will now contain a dot; and
it will be observed that the dots in sections perpendicular to BO
have arranged themselves in similar
paths. In this manner, p1, q1, r1
being placed in the corner cubelet
O, these letters are severally placed
in the cubelets of three different
paths of AOB, and again along
any similar paths in the seven
sections perpendicular to AO, starting
from the letters’ position in
AOB. Next, p2q2r2, p3q3r3, . . .
p7q7r7 are placed in the other cubelets
of the edge AO, and dispersed
in the same manner as p1q1r1.
Every cubelet will then be found to
contain a different combination of
the p’s, q’s and r’s. If therefore
the p’s are made equal to 1, 2,
. . . 7, and the q’s and r’s to 0,
1, 2, . . . 6, in any order, and the
q’s multiplied by 7, and the r’s
by 72, then, as in the case of the squares, the 73 cubelets will
contain the numbers from 1 to 73, and the Nasical summations will
be Σ72r + Σ7q + p. If 2, 4, 5 be values of r, p, q, the number for
that cubelet is written 245 in the septenary scale, and if all the
cubelet numbers are kept thus, the paths along which summations
are found can be seen without adding, as the seven numbers
would contain 1, 2, 3, . . . 7 in the unit place, and 0, 1, 2, . . . 6 in
each of the other places. In all Nasik cubes, if such values are given
to the letters on the central cubelet that the number is the middle
one of the series 1 to n3, the sum of all the pairs of numbers opposite
to and equidistant from the middle number is the double of it.
Also, if around a Nasik cube the twenty-six surrounding equal cubes
be placed with their cells filled with the same numbers, and their
corresponding faces looking the same way,—and if the surrounding
space be conceived thus filled with similar cubes, and a straight line
of unlimited length be drawn through any two cubelet centres, one
in each of any two cubes,—the numbers along that line will be found
to recur in groups of seven, which (except in the three cases where
the same p, q or r recur in the group) together make the Nasical
summation of the cube. Further, if we take n similarly filled
Nasik cubes of n, n new letters, s1, s2, . . . sn, can be so placed, one in
each of the n4 cubelets of this group of n cubes, that each shall
contain a different combination of the p’s, q’s, r’s and s’s.
 |
| Fig. 26. |
 | |
| Fig. 27. | Fig. 28. |
This is done by placing s1 on each of the n2 cubelets of the first cube that contain p1, and on the n2 cubelets of the 2d, 3d, . . . and nth cube that contain p2, p3, . . . pn respectively. This process is repeated with s2, beginning with the cube at which we ended, and so on with the other s’s; the n4 cubelets, after multiplying the q’s, r’s, and s’s by n, n2, and n3 respectively, will now be filled with the numbers from 1 to n4, and the constant summation will be Σn3s + Σn2r + Σnq + Σp. This process may be carried on without limit; for, if the n cubes are placed in a row with their faces resting on each other, and the corresponding faces looking the same way, n such parallelepipeds might be put side by side, and the n5 cubelets of this solid square be Nasically filled by the introduction of a new letter t; while, by introducing another letter, the n6 cubelets of the compound cube of n3 Nasik
