horizontal intensity of the earth’s force. The distance between the poles may with sufficient accuracy for a rough determination be assumed to be equal to five-sixths of the length of the magnet.
Measurement of Magnetization and Induction.—The magnetic condition assumed by a piece of ferromagnetic metal in different circumstances is determinable by various modes of experiment which may be classed as magnetometric, ballistic, and traction methods. When either the magnetization I or the induction B corresponding to a given magnetizing force H is known, the other may be found by means of the formula B = 4πI + H.
Magnetometric Methods.—Intensity of magnetization is most directly measured by observing the action which a magnetized body, generally a long straight rod, exerts upon a small magnetic needle placed near it. The magnetic needle may be cemented horizontally across the back of a little plane or concave mirror, about 14 or 38 in. in diameter, which is suspended by a single fibre of unspun silk; this arrangement, when enclosed in a case with a glazed front to protect it from currents of air, constitutes a simple but efficient magnetometer. Deflections of the suspended needle are indicated by the movement of a narrow beam of light which the mirror reflects from a lamp and focusses upon a graduated cardboard scale placed at a distance of a few feet; the angular deflection of the beam of light is, of course, twice that of the needle. The suspended needle is, in the absence of disturbing causes, directed solely by the horizontal component of the earth’s field of magnetic force HE, and therefore sets itself approximately north and south. The magnetized body which is to be tested should be placed in such a position that the force HP due to its poles may, at the spot occupied by the suspended needle, act in a direction at right angles to that due to the earth—that is, east and west. The direction of the resultant field of force will then make, with that of HE, an angle θ, such that Hp / HE = tan θ, and the suspended needle will be deflected through the same angle. We have therefore
The angle θ is indicated by the position of the spot of light upon the scale, and the horizontal intensity of the earth’s field HE is known; thus we can at once determine the value of HP, from which the magnetization I of the body under test may be calculated.
In order to fulfil the requirement that the field which a magnetized rod produces at the magnetometer shall be at right angles to that of the earth, the rod may be conveniently placed in any one of three different positions with regard to the suspended needle.
 |
| Fig. 6. |
(1) The rod is set in a horizontal position level with the suspended needle, its axis being in a line which is perpendicular to the magnetic meridian, and which passes through the centre of suspension of the needle. This is called the “end-on” position, and is indicated in fig. 6. AB is the rod and C the middle point of its axis; NS is the magnetometer needle; AM bisects the undeflected needle NS at right angles. Let 2l = the length of the rod (or, more accurately, the distance between its poles), v = its volume, m and −m the strength of its poles, and let d = the distance CM. For most ordinary purposes the length of the needle may be assumed to be negligible in comparison with the distance between the needle and the rod. We then have approximately for the field at M due to the rod
| HP = | m | − | m | = m | 4dl | . |
| (d − l)2 | (d + l)2 | (d 2 − l 2)2 |
Therefore
| 2ml = M = | (d 2 − l 2)2 HP | = | (d 2 − l 2)2 HE tan θ | . |
| 2d | 2d |
And
| I = | M | = | (d 2 − l 2)2 HE | tan θ, |
| v | 2dv |
whence we can find the values of I which correspond to different angles of deflection.
(2) The rod may be placed horizontally east and west in such a position that the direction of the undeflected suspended needle bisects it at right angles. This is known as the “broadside-on” position, and is represented in fig. 7. Let the distance of each pole of the rod AB from the centre of the magnetometer needle = d. Then, since HP, the force at M due to m and −m, is the resultant of m/d 2 and −m/d 2, we have
| HP | = | 2l |
| m/d 2 | d |
or
| HP = | 2ml | , |
| d 3 |
the direction being parallel to AB.
And
| I = | d 3HP | = | d 3HE | tan θ. |
| v | v |
 | |
| Fig. 7. | Fig. 8. |
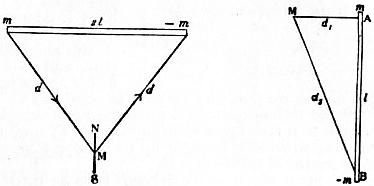
(3) In the third position the test rod is placed vertically with one of its poles at the level of the magnetometer needle, and in the line drawn perpendicularly to the undeflected needle from its centre of suspension. The arrangement is shown in fig. 8, where AB is the vertical rod and M indicates the position of the magnetometer needle, which is supposed to be perpendicular to the plane of the paper. Denoting the distance AM by d1, BM by d2, and AB by l, we have for the force at M due to the magnetism of the rod
| HP = | m | − horizontal component of | m |
| d12 | d22 |
| = m { | 1 | − | d1 | ). |
| d12 | d23 |
Therefore
| m = | HP | = | d12HE | tan θ, |
| (1 / d12) − (d1 / d23) | 1 − (d1 / d2)3 |
and
| I = | ld12 HE | tan θ. |
| v {1 − (d1 / d2)3 } |
This last method of arrangement is called by Ewing the “one-pole”
method, because the magnetometer deflection is mainly caused by
the upper pole of the rod (Magnetic Induction, p. 40). For experiments
with long thin rods or wires it has an advantage over the
other arrangements in that the position of the poles need not be
known with great accuracy, a small upward or downward displacement
having little effect upon the magnetometer deflection. On
the other hand, a vertically placed rod is subject to the inconvenience
that it is influenced by the earth’s magnetic field, which is not
the case when the rod is horizontal and at right angles to the magnetic
meridian. This extraneous influence may, however, be eliminated
by surrounding the rod with a coil of wire carrying a current
such as will produce in the interior a magnetic field equal and
opposite to the vertical component of the earth’s field.
If the cardboard scale upon which the beam of light is reflected by the magnetometer mirror is a flat one, the deflections as indicated by the movement of the spot of light are related to the actual deflections of the needle in the ratio of tan 2θ to θ. Since θ is always small, sufficiently accurate results may generally be obtained if we assume that tan 2θ = 2 tan θ. If the distance of the mirror from the scale is equal to n scale divisions, and if a deflection θ of the needle causes the reflected spot of light to move over s scale divisions, we shall have
We may therefore generally substitute s/2n for tan θ in the various expressions which have been given for I.
 |
| Fig. 9. |
Of the three methods which have been described, the first two are generally the most suitable for determining the moment or the magnetization of a permanent magnet, and the last for studying the changes which occur in the magnetization of a long rod or wire when subjected to various external magnetic forces, or, in other words, for determining the relation of I to H. A plan of the apparatus as arranged by Ewing for the latter purpose is shown diagrammatically in fig. 9. The cardboard scale SS is placed above a wooden screen, having in it a narrow vertical slit which permits a beam of light from the lamp L to reach the mirror of the magnetometer M, whence it is reflected upon the scale. A is the upper end of a glass tube, half a metre or so in length, which is clamped in a vertical position behind the magnetometer. The tube is wound over its whole length with two separate coils of insulated wire, the one being outside the other. The inner coil is supplied, through the intervening apparatus, with current from the battery of secondary cells B1; this produces the desired magnetic field inside the tube. The outer coil derives current, through an adjustable resistance R, from a
