Page:EB1911 - Volume 25.djvu/850

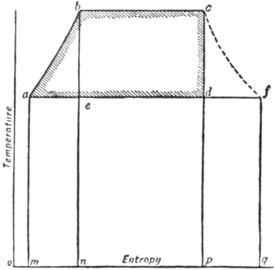
Values of the entropy of water and steam are given in the table. The entropy-temperature diagram for a Rankine cycle is illustrated in fig. 11, where 𝑎𝑏, a logarithmic curve, represents the process of heating the feed-water, and 𝑏𝑐 the passage from the state of water into that of steam. The diagram is drawn to scale for a case in which steam is formed at a pressure of 180 ℔ per sq. in., and condensed at a pressure of 1 ℔ per sq. in. After the formation of the steam, the next step in the ideal process is adiabatic expansion from the higher to the lower limit of temperature, which is represented by the vertical straight line 𝑐𝑑, an adiabatic process being also isentropic. Finally, the cycle is completed by 𝑑𝑎, which represents the condensation of the steam after its temperature has been reduced by adiabatic expansion to the lower limit of temperature. The area 𝑎𝑏𝑐𝑑 represents the work done, and its value per ℔ of steam is identical with W as reckoned above. The area 𝑚𝑎𝑏𝑐𝑝 is the whole heat taken in, and the area 𝑚𝑎𝑑𝑝 is the heat rejected.

Fig. 11

Let a curve 𝑐𝑓 be drawn to show the values of the entropy of steam for various temperatures of saturation: then if 𝑎𝑑 be produced to meet the curve in 𝑓, the ratio 𝑓𝑑/𝑓𝑎 represents the fraction of the steam which was condensed during adiabatic expansion. For the point 𝑓 represents the state of 1 ℔ of saturated steam, and in the condensation of 1 ℔ of saturated steam the heat given out would be the area under 𝑓𝑎, whereas the heat actually given out in the condensation from 𝑑 was the area under 𝑑𝑎. Thus the state at 𝑑 is that of a wet mixture in which 𝑑𝑎/𝑓𝑎 represents the fraction present as steam, and 𝑓𝑑/𝑓𝑎 the fraction present as water. It obviously follows that by drawing horizontal lines at intermediate temperatures the development of wetness in the expanding steam can be readily traced. Again, if the steam is not dry when expansion begins, its state may be represented by making the expansion line begin at a point in the line 𝑏𝑐, such that the segments into which the line is divided are proportional to the constituents of the wet mixture. In this way the ideal process may be exhibited for steam with any assumed degree of initial wetness. Further, the entropy-temperature diagram admits of ready application to the case of incomplete expansion. Suppose, for example, that after adiabatic expansion from 𝑐 to 𝑐′ (fig. 12) the steam is directly cooled to the lower-limit temperature by the application of cooling water instead of by continued expansion. This process is represented by the line 𝑐′𝑒𝑑, which is a curve of constant volume. Its form is determined by the consideration that at any point 𝑒 the proportion of steam still uncondensed, or 𝑙𝑒/𝑙𝑘, is such that the mixture fills the same volume as was filled at 𝑐′.

Fig. 12

43. Entropy-Temperature Diagrams extended to the Case of Superheated Steam.—In the diagrams which have been sketched, it has been assumed that the steam is supplied to the engine in a saturated state. To extend the same treatment to the case of superheated steam, we have to take account of the supplementary supply of heat which the steam receives after the point 𝑐 is reached, and before expansion begins. When superheating is resorted to, as is now often the case in practice, the superheat is given at constant pressure. If κ represent as before the mean specific heat of steam at constant pressure, the addition of entropy during the process of superheating from τ₁ to τ′ is κ(τ′ − τ₁). The value of κ may be treated as approximately constant, and the addition to the entropy may then be written as κ(log τ − log τ₁). This gives a line such as 𝑐𝑟 on the entropy diagram (fig. 13), and increases the value of W by the amount

$\int _{\tau _{1}}^{\tau '}{\frac {\kappa d\tau (\tau -\tau _{2})}{\tau }}$

which is represented on the diagram by the area 𝑑𝑐𝑟𝑠. During adiabatic expansion from 𝑟 the steam remains superheated until it reaches the state 𝑡, when it is just saturated, and further expansion results in the condition of wetness indicated by 𝑠. The extra work 𝑑𝑐𝑟𝑠 is done at the expense of the extra supply of heat 𝑝𝑐𝑟𝑢, and an inspection of the diagram suffices to show that the efficiency of the ideal cycle is only very slightly increased by even a large amount of superheating. In practice, however, superheating does much to promote efficiency, because it materially reduces the amount by which the actual performance of an engine falls short of the ideal performance by keeping the steam comparatively dry in its passage through the engine, and thereby reducing exchanges ot heat between the steam and the metal.

Fig. 13

44. Entropy of Wet Steam.—The entropy of wet steam is readily calculated by considering that the change of entropy in the conversion from water to steam will be 𝑞L/τ if the steam is wet, 𝑞 being the dryness Accordingly the entropy of wet steam at any temperature τ is σ(log_ετ − log_ετ₀)+𝑞L/τ. Further, since σ for water is practically equal to unity this expression may be written

φ＝log_ετ − log_ετ₀+𝑞L/τ.

We may apply this expression to trace the development of wetness in steam when it expands adiabatically. In adiabatic expansion φ＝constant. Using the suffix 1 to distinguish the initial state, we therefore have at any stage in the expansion

log_ετ − log_ετ₀＝log_ετ₁ − log_ετ₀ +𝑞₁L₁/τ₁,

from which the dryness at that stage is found, namely,

𝑞＝τ/L(𝑞₁L₁/τ₁ + log_ετ₁/τ₁).

The expression is not applicable to steam which is initially superheated. In either case the graphic method of tracing the change of condition during adiabatic expansion is available.

45. Actual Performance.—Trials of engines using saturated steam show that in the most favourable cases from 60 to 65% of the ideally possible amount of work is realized as “indicated” work One of the causes of loss is that the expansion is incomplete. In practice the steam is allowed to escape to the condenser, while its pressure is still considerably higher than the pressure at which condensation is to take place. When the pressure of steam in the cylinder has been so far reduced by expansion that it can only overcome the friction of the piston, there is no advantage in going on further; the indicated work due to any additional expansion would add nothing to the output of the engine, when allowance is made for the work spent on friction within the mechanism itself. Considerations of bulk often lead to an even earlier release of the expanding steam; and another consideration which points the same way is that when expansion is carried very far, the losses due to exchange of heat between the cylinder and the steam, referred to below, tend to increase. Again, since experience shows that the most efficient engines are those in which the process of expansion is divided into two, three or more stages by the use of compounded cylinders, a certain amount of loss is to be ascribed to the drops in pressure which are liable to occur through unresisted expansion in the transfer of steam from one vessel to another. But the chief cause of loss is to be found in the exchanges of heat which take place between the steam and the metal. In each cylinder there is a process of alternate condensation and re-evaporation—condensation during the period of admission, when the steam finds itself brought into contact with metal which has been chilled by evaporation during the preceding exhaust stroke, and then evaporation, when the pressure has fallen sufficiently, during the later stage of expansion, as well as during exhaust. The consequence is that the steam though supplied in a dry
Fig. 14 state, may contain some 20 or 30% of moisture when admission to the cylinder is complete, and the entropy diagram for the real process of expansion takes a form such as is indicated by the line 𝑐′𝑐″ in fig. 14. The heat supplied is still measured by the area under 𝑎𝑏𝑐. The condensation from 𝑐 to 𝑐′ occurs by contact with the walls of the cylinder; and though part of the heat thus abstracted is restored before release occurs at 𝑐″ , the general result is to make a large reduction in the area of the diagram.

46. Exchanges of Heat between the Steam and the Metal.—The exchanges of heat between steam and metal in the engine cylinder have been made the subject of an elaborate experimental examination