right angles as the figure has sides, less four; the second is linear,
viz. the algebraical sum of the x co-ordinates and that of the y
co-ordinates should each be = o. The astronomical test is this:
at any station of the traverse the azimuth of a referring mark may
be determined by astronomical observations; the inclination of
the line between the station and the referring mark to the meridian
of the origin is given by the traverse; the two should differ by the
convergency of the meridians of the station and the origin. In
practice the angles of the traverse arc usually adjusted to satisfy
their special geometrical and astronomical tests in the first instance,
and then the co-ordinates of the stations are calculated and adjusted
by corrections applied to the longest, that the angles may be least
disturbed, as no further corrections are given them.
The exact value of the convergence, when the distance and azimuth of the second astronomical station from the first are known, is that of B(π+A) of equation (5); Meridians, but, as the first term is sufficient for a traverse, we have
convergency = x tan λ cosec11″/λ,
substituting x, the co-ordinate of the second station perpendicular to the meridian of the origin, for c sin A.
The co-ordinates of the principal stations of a trigonometrical survey are usually the spherical co-ordinates of latitude and longitude; those of a traverse survey are always rectangular, plane {or a small area but spherical for a large one. It is often necessary, therefore, for purposes of comparison and check at stations common to surveys of both descriptions, to convert either rectangular co-ordinates into latitudes and longitudes, or vice versa,
in order that the errors of traverses may be dispersed by proportion over the co-ordinates of the traverse stations, if desired, or adjusted in the final mapping. The latter is generally all that is necessary, more particularly when the traverses are referred to successive trigonometrical stations as origins, as the operations arc being extended, in order to prevent any large accumulation of error. Similar conversions are also frequently necessary in map projections. The method of effecting them will now be indicated.

Fig. 5.
Let A and B be any two points, Aa the meridian of A, Bb the parallel of latitude of B; then Ab, Bb will be their differences in latitude and longitude; from B draw BP perpendicular to Aa; then AP, BP will be the rectangular spherical co-ordinates. of B relatively to A. Put BP = x, AP = y, the arc Pb=η, and the arc Bb, the difference of longitude, = ω; also let λa, X& and X, be the latitudes of A, B, and the point P, p p the radius of curvature of the meridian, and v, the normal ter- minating in the axis minor for the latitude X p; and Fig. 5. Jet Po be the radius of curvature for the latitude Jfaa+Xp). Then, when the rectangular co-ordinates are given, we have, taking A as the origin, the latitude of which is known,
X p = X„ + A;oscc r
2p p v p
tan X p cosec 1' (19).
Xt — X =*— cosec l"—rf, u=— sec(\b+iv) cosec 1" (20). po v p
And, when the latitude and longitude are given, we have [1]
'"=(f)S sin2 ^ sin, l
y =Po{Xi — X„ + r;)sin l" [
x= a>KpCOs(X&-t-$7;)sin '"J
When a hill peak or other prominent object has been observed from a number of stations whose co-ordinates are already fixed, the converging rays may be projected graphically, and from an examination of their several intersections the most probable position of the object may be obtained almost as accurately as by calculations by the method of least squares, which are very laborious and out of place for the deter- mination of a secondary point. The following is a description of the application of this method to points on a plane surface in the calculations of the ordnance survey. Let $1, St, . . . be stations whose rectangular co-ordinates, Xi, * 2 , . . . perpendicular, and y\, yt, . . . parallel, to the meridian of the origin are given; let Ci, ch, be the bearings — here the direction-inclinations with the meridian of the origin — of any point P, as observed at the several stations; and let p be an approximate position of P, with co-ordinates x T \ y p , as determined by graphical projection on a district map or by rough calculation. Construct a diagram of the rays converging around p, by taking a point to represent p and drawing two lines through it at right angles to each other to indicate the directions of north, south, east and west. Calculate accurately (yp − y1) tan a1 and compare with (x,—xi); the differ- ence will show how far the direction of the ray from si falls to the east or west of p. Or calculate (x p — x{) cot a1, and compare with (yp − y1) to find how far the direction falls to the north or south of p. Set off the distance on the corresponding axis of p, and through
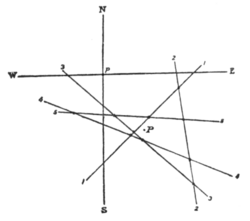
Fig. 6.
the point thus fixed draw the direction ai with a common protractor. All the other rays around p may be drawn in like manner; they will intersect each other in a number of points, the centre of which may be adopted as the most probable position of P. The co-ordinates of P will then be readily obtained from those of £=*=the distances on the meridian and perpendicular. In the annexed diagram (fig. 6) P is supposed to have been observed from five stations, giving as many intersecting rays, (1, 1), (2, 2), . . .; there are ten points of intersection, the mean position of which gives the true position of P, the assumed position being p. The advantages claimed for the method are that, the bearings being_ independent, an erroneous bearing may be redrawn without disturbing those that are correct; similarly new bearings may be introduced without disturbing previous work, and observations from a large number of stations may be readily utilized, whereas, when calculation is resorted to, observations in excess of the minimum number required are frequently rejected because of the labour of computing them.
Authorities. — Clarke, Geodesy (London); Waller, " India's Contribution to Geodesy," Trans. Roy. Soc, vol. clxxxvi. (1895); Thuillier, Manual of Surveying for India (Calcutta); Gore, Hand- book of Professional Instructions for the Topographical Branch Survey of India Department (Calcutta); D'A. Jackson, Aid to Survey Practice (London, 1899); Woodthorpe, Hints to Travellers (Plane-tabling section); Grant, "Diagram for Determining Paral- laxes," &c, Geog. Journ. (June 1896); Pierce, "Economic Use of the Plane-Table," vol. xcii. pt. ii., Pro. Inst. Civ. Eng.; Bridges- Lee, Photographic Surveying (1899); London Society of Engineers; Laussedat, Recherches sur les instruments les mithodes el le dessin topographique (Paris, 1898); H. M. Wilson, Topographic Surveying (New York, 1905); Professional Papers Royal Engineers (occasional paper series), vol. xiii. paper v. by Holdich; vol. xiv. paper ii. by Talbot; vol. xxvi. paper 1. by MacDonnell (R.E. Institute, Chatham). (T. H. H.*)
6. Nautical Surveying
The great majority of nautical surveys are carried out by H.M. surveying vessels under the orders of the hydrographer of the admiralty. Plans of harbours and anchorages are also received from H.M. ships in commission on foreign stations, but surveys of an extended nature can hardly be executed except by a ship specially fitted and carrying a trained staff of officers. The introduction of steam placed means at the disposal of nautical surveyors which largely modified the conditions under which they had to work in the earlier days of sailing vessels, and it has enabled the ship to be used in various ways previously impracticable. The heavy draught of ships in the present day, the growing increase of ocean and coasting traffic all over the world, coupled with the desire to save distance by rounding points of land and other dangers as closely as possible, demand surveys on larger scales and in greater detail than was formerly necessary; and to meet these modern requirements resurveys of many parts of the world are continually being called for. Nautical surveys vary much in character according to the nature of the work, its importance to navigation, and the time available. The elaborate methods and rigid accuracy of a triangulation for geodetic purposes on shore are unnecessary,
- ↑ In the Indian survey, tables are employed for these calculations which give the value of 1″ of arc in feet on the meridian, and on each parallel of latitude, at intervals of 5' apart; also a corresponding table of arc-versines {Pb) of spheroidal arcs of parallel (Bb) 1° in length, from which the arc-versines for shorter or longer arcs are obtained proportionally to the squares of the arcs; x is taken as the difference of longitude converted into linear measure.

