ED′ is one-half of the distance ED, and so on in proportion. The distance ED can be instantly inferred from the readings of the staff, if the latter be suitably graduated. If, for example, it be desired to know the distance ED in yards, and by construction the proportion EC/BC=50, then the intercept on the staff at 1 yard from E would be 1/50th of a yard, or ·72 inch, the intercept at 2 yards from E would be 2X·72 inches, and so on. If therefore the staff be graduated with divisions of ·72 inch, and the intercept be 45 of such divisions, it would be inferred that the distance of the staff from E was 45 yards. The constant proportion EC/BC can be checked by measuring 100 yards from E and observing whether the intercept is exactly 100 divisions or not.
If it is not, the wire diaphragm must be shifted in the tube until it is. In figs. 3, 4, 5 and) 6 the distances are deduced from the readings of a central wire in the optical axis of the telescope and of a wire above it, for the sake of simplicity. The usual arrangement is to fit the diaphragm with a central wire and with one or two wires above and below it at equal distances from the central wire. The vertical angle of depression or elevation is fixed by directing the central wire to a well-defined division on the staff, and the distance of the staff is inferred from the readings given by the corresponding wires above and below the central wire.
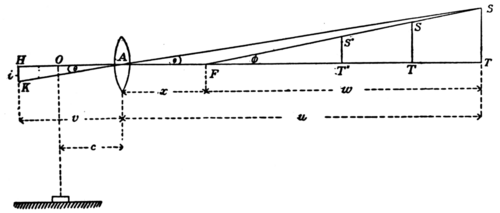
The elementary form of tachometer given above illustrates the general principle of the class of tachometers now under consideration, and as leading up to the practical form, in which the staff is viewed with a telescope mounted in the manner of a theodolite. The simplest form is Reichenbach's tachometer, which may be investigated as follows:—In fig. 4 let A be the object glass by which an image of the staff ST is formed at HK. The wire diaphragm is moved in the tube so as to coincide with the image,
and the image and wires are viewed with an eye-piece (not shown) in the usual way. Let O be the point where the vertical axis of the instrument cuts the axis of the telescope, the instrument being centred over a pe, from which the distance to the staff is required. The object glass fiif focal length = 𝑓) is at a distance 𝑐 from O. Let AT=𝑢 and AH=𝑣, and the angle SAT=HAK=θ. Then if 𝑖 be the height of the image HK, 𝑖=𝑣 tan θ. Since 1/𝑣+𝑖/𝑢=1/𝑓 we have 𝑣= -𝑢𝑓/(𝑢−Q, and hence i=uf tan θ/(𝑢−𝑓). Let F be some point on AT such that AF =𝑥 and FT =𝑢′. And let the angle SFT =φ. Then 𝑢 =𝑢′+𝑥 and tan θ=𝑢′ tan φ/(𝑢′+𝑥), and therefore
i= (𝑢′+𝑥)𝑓/𝑢′+𝑥−𝑓 {=u, +x fé. tan¢=$tan 4>; and, if x=f, i=f tan ¢.
If therefore the point F be taken at a distance 𝑓 from the object glass, every intercept of the staff for positions between T and F, such as S′T′, S″T″, &c., which are bounded by the V line FS, and for which consequently θ is the same, will have the same height of image at the diaphragm. Conversely, if K be a wire in the diaphragm it will cut the image of the staff for all positions of the staff between T and F in points H object glass, were it not that the rays, after passing through the object glass, are received by the anal lat tic lens and the image of the staff is formed at K on the wire diaphragm, which is slid in the tube till it coincides with the position of the image. The image at K is viewed by an eye-piece in the usual way. Let T be the point where the image of the staff is cut by the central wire of the diaphragm, and S the point where the image is cut by one of the outer wires of the diaphragm. If 0 and ¢ be the angles subtended by ST at the object glass and at the point O respectively, and if i be the height of the image at K, h the height of the virtual image at H, then by elementary geometry and from optical considerations, we obtain i= f 1/f'f". » . -tan4>
"'(fi-d-hfz)"16f1'(C+f1)ld"J'2>i
Let fz be made such that of, -(c-{-fl) (d-f2)=0, the equation of condition above mentioned. Then fg ={d(c-l-fl) -cf1}/(C-|-fl). And i= .tan ¢= - tan ¢.
that lie on the line FS. Now the intercept S"T", half-way, L between F and T, will be one-half of ST, and therefore if the reading on the staff indicated by the wire in question be one-half of ST, it may be inferred that the position of the staff is half-way between F and T, and similarly for other distances. If the distance of ST from O is required, as is usually the case, a quantity f+c must be added to every distance from F determined as above.
It is very seldom that the line of sight AT of the telescope is at right angles to the staff. In general it is more or less inclined to the staff, which is almost always held vertical, and the horizontal and vertical distances of the staff from the axis of rotation of the telescope are found thus:—In fig. 5 let ST be the observed intercept on the staff when the telescope is inclined at an angle 𝑎 to the horizontal. Draw TS′ at right angles to OT. The angle TS′S will be very nearly a right angle, and STS′ may be taken as equal to 𝑎. If there were 𝑛 graduations (each corresponding to 1 yard in distance) in ST, there would be 𝑛 cos 𝑎 graduations in

Fig. 5.
S′T, and therefore the distance of the staff from F, as inferred from the observed number of graduations in ST, must be multiplied by cos 𝑎. to give the true distance FT. Again FN =FT cos 𝑎, so that the distance inferred from the observed number of graduations in ST must be multiplied by cosza. to give the horizontal distance of F from T. To this must be added the distance OL=OF cos 𝑎(f+c) cos a to get the horizontal distance, OM, of O (the vertical axis of the instrument) from T. This value of OM must be multiplied by tan a to obtain the value of h, the vertical distance of T from O. Tables of the value of cos 𝑎, cos2 𝑎, and tan 𝑎 are necessary to facilitate these calculations.
In this tachometer the distances as inferred from the readings of the staff are the distances of the staff from F and not from O. This defect was remedied by Porro, who added a lens (called the anallattic lens) to the telescope. The arrangement of the telescope as manufactured by Messrs Troughton and Simms, is as follows:—In fig. 6 O is the point where the vertical axis of the instrument cuts the axis of the telescope. The object glass is fixed at a distance 𝑐 from O, and the anallattic lens at a distance 𝑑 from the object glass. The distances 𝑐 and 𝑑 are chosen to suit the constructive conveniences of the instrument. The diaphragm at K is movable so that it can be made to coincide with the image of the staff. The focal length 𝑓1 of the object glass is arbitrary, and the focal length 𝑓2 of the anallattic lens is determined from an equation of condition between 𝑐, 𝑑, 𝑓1, and 𝑓2. The image of the staff ST would be formed by the object glass at H, at a distance 𝑣1 from the
Therefore all the readings of the staff which would be given by the outer wire of the diaphragm will lie on the line OS (for all of