The differential of a function equals its derivative multiplied by the differential of the independent variable.
Let us illustrate what this means geometrically.
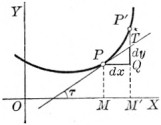
Let be the derivative of at P. Take , then
Therefore , or , is the increment (= QT) of the ordinate of the tangent corresponding to dx.[1]
This gives the following interpretation of the derivative as a fraction.
If an arbitrarily chosen increment of the independent variable x for a point P(x, y) on the curve y = f(x) be denoted by dx, then in the derivative
dy denotes the corresponding increment of the ordinate drawn to the tangent.
89. Infinitesimals. In the Differential Calculus we are usually concerned with the derivative, that is, with the ratio of the differentials dy and dx. In some applications it is also useful to consider dx as an infinitesimal (see §15), that is, as a variable whose values remain numerically small, and which, at some stage of the investigation, approaches the limit zero. Then by (B), §88, and (2), §20, dy is also an infinitesimal.
In problems where several infinitesimals enter we often make use of the following
Theorem. In problems involving the limit of the ratio of two infinitesimals, either infinitesimal may be replaced by an infinitesimal so related to it that the limit of their ratio is unity.
Proof. Let be infinitesimals so related that
| (C) | limit and limit . |
- ↑ The student should note especially that the differential (= dy) and the increment (= dy) of the function corresponding to the same value of dx () are not in general equal. For, in the figure, , but .














