Page:Elements of the Differential and Integral Calculus - Granville - Revised.djvu/166

Third Step. Differentiate with respect to the time.

Fourth Step. Make a list of the given and required quantities.

Fifth Step. Substitute the known quantities in the result found by differentiating (third step), and solve for the unknown.

EXAMPLES

1. A man is walking at the rate of 5 miles per hour towards the foot of a tower 60 ft. high. At what rate is he approaching the top when he is 80 ft. from the foot of the tower?

Example 2 illustration.

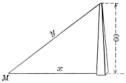
Solution. Apply the above rule.
First step. Draw the figure. Let x = distance of the man from the foot and y = his distance from the top of the tower at any instant.
Second step. Since we have a right triangle,
$\ y^{2}$	$=x^{2}+3600\$.
Third step. Differentiating, we get
$2y{\frac {dy}{dt}}$	$=2x{\frac {dx}{dt}}$, or,
(A) ${\frac {dy}{dt}}$	$={\frac {x}{y}}{\frac {dx}{dt}}$, meaning that at any instant whatever
(Rate of change of y)	= $\left({\frac {x}{y}}\right)$ (rate of change of x).

Fourth step.	$\ x$	$=80,\$	${\frac {dx}{dt}}$	$=5\$ miles an hour,
				= 5 × 5280 ft. an hour.
	$y$	$={\sqrt {x^{2}+3600}}$	${\frac {dy}{dt}}$	= ?
		= 100.
Fifth step.	Substituting back in (A),
	${\frac {dy}{dt}}$	= ${\frac {80}{100}}\times 5\times 5280$ ft. per hour
		= 4 miles per hour. Ans.

2. A point moves on the parabola $6y=x^{2}$ in such a way that when x = 6, the abscissa is increasing at the rate of 2 ft. per second. At what rates are the ordinate and length of arc increasing at the same instant?

Solution First step. Plot the parabola.
Second step.	$\ 6y$	$=x^{2}\$
Third step.	$6{\frac {dy}{dt}}$	$=2x{\frac {dx}{dt}}$, or,
(B)	${\frac {dy}{dt}}$	$={\frac {x}{3}}\cdot {\frac {dx}{dt}}$.
This means that at any point on the parabola
(Rate of change of ordinate)		= $\left({\frac {x}{3}}\right)$(rate of change of abcissa).