Page:Elements of the Differential and Integral Calculus - Granville - Revised.djvu/179

CURVATURE. RADIUS OF CURVATURE

99. Curvature. The shape of a curve depends very largely upon the rate at which the direction of the tangent changes as the point of contact describes the curve. This rate of change of direction is called curvature and is denoted by K. We now proceed to find its analytical expression, first for the simple case of the circle, and then for curves in general.

100. Curvature of a circle. Consider a circle of radius R. Let

$\tau$	= angle that the tangent at P makes with OX; and
$\tau +\Delta \tau$	= angle made by the tangent at a neighboring point P'.
Then we say
$\Delta \tau$	= total curvature of arc PP'.

Curvature of a circle.

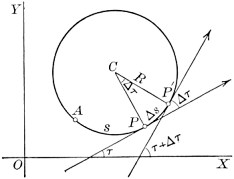
If the point P with its tangent be supposed to move along the curve to P', the total curvature (= $\Delta \tau$) would measure the total change in direction, or rotation, of the tangent; or, what is the same thing, the total change in direction of the arc itself. Denoting by s the length of the arc of the curve measured from some fixed point (as A) to P, and by $\Delta s$ the length of the arc P P', then the ratio

${\frac {\Delta \tau }{\Delta s}}$

measures the average change in direction per unit length of arc.^[1] Since, from the figure,

$\Delta s=R\cdot \Delta \tau ,$

or

${\frac {\Delta \tau }{\Delta s}}={\frac {1}{R}},$

1. Thus, if $\Delta \tau ={\frac {\pi }{6}}$ radians (= 30°), and $\Delta s$ = 3 centimeters, then ${\tfrac {\Delta \tau }{\Delta s}}={\tfrac {\pi }{18}}$ radians per centimeter = 10° per centimeter = average rate of change of direction.