Page:Elements of the Differential and Integral Calculus - Granville - Revised.djvu/206

Now consider the function of $x$ defined by

$\phi (x)=(x-\alpha ')+(y-\beta '){\frac {dy}{dx}},$

in which $y$ has been replaced by $f(x)$ from (A).

Then equations (B) show that

$\phi (x_{0})=0,\ \phi (x_{1})=0.$

But then, by Rolle's Theorem (§105), $\phi '(x)$ must vanish for some value of $x$ between $x_{0}$ and $x_{1}$ say $x'$. Therefore $\alpha '$ and $\beta '$ are determined by the two equations

$\phi (x_{0})=0,\ \phi '(x')=0.$

If now $P_{1}$ approaches $P_{0}$ as a limiting position, then $x'$ approaches $x_{0}$, giving

$\phi (x_{0})=0,\ \phi '(x_{0})=0;$

and $C'(\alpha ',\beta ')$ will approach as a limiting position the center of curvature $C(\alpha ,\beta )$ corresponding to $P_{0}$ on the curve. For if we drop the subscripts and write the last two equations in the form

$(x-\alpha ')+(y-\beta '){\frac {dy}{dx}}=0,$

$1+\left({\frac {dy}{dx}}\right)^{2}+(y-\beta '){\frac {d^{2}y}{dx^{2}}}=0,$

it is evident that solving for $\alpha '$ and $\beta '$ will give the same results as solving (B) and (C), § 116, for $\alpha$ and $\beta$. Hence

Theorem. The center of curvature C corresponding to a point P on a curve is the limiting position of the intersection of the normal to the curve at P with a neighboring normal.

Locus of centers of curvature.

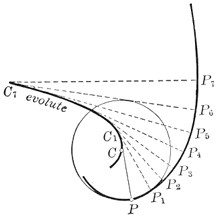
119. Evolutes. The locus of the centers of curvature of a given curve is called the evolute of that curve. Consider the circle of curvature corresponding to a point P on a curve. If P moves along the given curve, we may suppose the corresponding circle of curvature to roll along the curve with it, its radius varying so as to be always equal to the radius of curvature of the curve at the point P. The curve $CC_{7}$ described by the center of the circle is the evolute of $PP_{7}$ It is instructive to make an approximate construction of the evolute of a curve by estimating (from the shape of the curve) the lengths