Illustrative Example 3. Find the rectangular equation of the envelope of the
straight line , where the slope is the variable parameter.
Solution.
First Step. .
Solving, .
- Substitute in the given equation,
.
- and squaring, , a parabola, is the equation of the envelope. The family of straight lines formed by varying the slope is shown in the figure, each line being tangent to the envelope, for we know from Analytic Geometry that is the tangent to the parabola expressed in terms of its own slope .
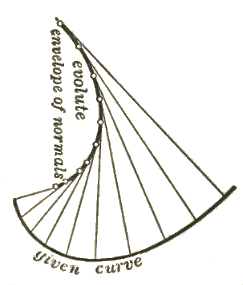
132. The evolute of a given curve considered as the envelope of its normals. Since the normals to a curve are all tangent to the evolute, §118, p. 181, it is evident that the evolute of a curve may also be defined as the envelope of its normals; that is, as the locus of the ultimate intersections of neighboring normals. It is also interesting to notice that if we find the parametric equations of the envelope by the method of the previous section, we get the coordinates and of the center of curvature; so that we have here a second method for finding the coordinates of the center of curvature. If we then eliminate the variable parameter, we have a relation between and which is the rectangular equation of the evolute (envelope of the normals).
- Illustrative Example 1. Find the evolute of the parabola considered as the envelope of its normals.
- Solution. The equation of the normal at any point is
- from (§2), p. 77. As we are considering the normals all along the curve, both and will vary. Eliminating by means of , we get the equation of the normal to be
(A) .