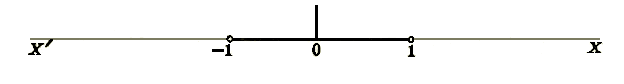This page needs to be proofread.
Substituting in (B), we get
which is an alternating series that converges.
Substituting in (B), we get
which is convergent by comparison with the p series ().
The series in the above example is said to have as the interval of convergence. This may be written , or indicated graphically as follows:
EXAMPLES
For what values of the variable are the following series convergent?
| Graphical representation of intervals of convergence[1] | |||
|---|---|---|---|
| 15. | Ans. | 
| |
| 16. | Ans. | 
| |
| 17. | Ans. | 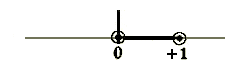
| |
| 18. | Ans. | 
| |
| 19. | Ans. All values of . | 
| |
| 20. | Ans. All values of . | 
| |
| 21. | Ans. All values of . | 
| |
| 22. | Ans. All values of . | 
|
- ↑ End points that are not included in the interval of convergence have circles drawn around them.






![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)