loose body, so circumstanced with reference to form and base, as to be overthrown by an earthquake shock (i. e. by a simple impulse), may be regarded as a compound pendulum. As the force of the inertia of motion is always , and for the same body proportionate to simply, so the body may be considered as if struck at its centre of gravity by another body (without loss of vis vivâ by impact, &c.) of a weight equal to its own, and moving with an horizontal velocity = . We exclude from investigation, bodies of wholly irregular figure, as such are not fitted for observation, and limit ourselves to such regular forms—prisms, cylinders, pyramids, &c.—as are found in connection with architectural structures or civil life, and are adapted for seismometry.
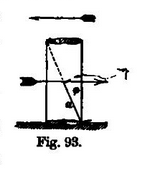
In order to upset the body, the horizontal velocity impressed by the shock (whatever be the duration of the latter) must be sufficient to make it turn upon one of the arris's or angles of its base, through an angle formed by the line, Fig. 93, joining the centre of gravity with that angle or arcis, and the vertical through it.
Let denote the distance (in feet) of this point or edge from the centre of gravity, then the statical work done in upsetting the body, whose weight is
This must equal the dynamical work acquired, which (as is well known), is equal to the work stored up in the centre of gyration, or—









