Page:MajoranaEmission1.djvu/3

above-mentioned hypothesis or mechanical theory and the relativistic one. It is indeed possible to see that some method, one moreover already in use, adopted for the verification of Doppler's principle may serve for the solution of the above-quoted problem.

In order to see this, let us consider a luminous source S which emits waves of length λ and of frequency n moving towards the observer fixed at O (fig. I). If we suppose

Fig. 1.

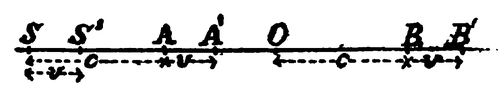
that the waves are transmitted through a stationary æther, the n waves emitted in a second by S will be distributed over the segment S'A = c — v. In the same time all the n waves distributed in the segment OB = c will have passed through O; we have therefore

${\frac {c-v}{n}}={\frac {c}{n}}$, or $n'=n{\frac {c}{c-v}}$.

If we put v/c = β and neglect terms of higher order than the first in β we have

n' = n(1 + β).

The new wave-length is obtained by the relations

c = nλ = n'λ':

λ' = λ(1 - β).

If now instead of the hypothesis of a stationary medium we adopt the ballistic or emissive hypothesis of which we have spoken above, we shall find that in one second the n waves emitted by S will be distributed over the segment S'A' = c. In the same time there will pass through O, n' waves which will be distributed over the segment OB' = c + v. We have, therefore,

${\frac {c}{n}}={\frac {c+v}{n'}}$, or n' = n(1 + β).

And since c = nλ and c + v = n'λ' we see that, in this case, λ' = λ.

As regards the frequency we arrive, therefore, at the same conclusions (with the exception of the terms in β²) whether we adopt the æthereal or the ballistic hypothesis; but for the wave-length we obtain different values from the two