If a body impinge upon another, and by its force change the motion of the other, that body also (because of the equality of the mutual pressure) will undergo an equal change, in its own motion, towards the contrary part. The changes made by these actions are equal, not in the velocities but in the motions of bodies; that is to say, if the bodies are not hindered by any other impediments. For, because the motions are equally changed, the changes of the velocities made towards contrary parts are reciprocally proportional to the bodies. This law takes place also in attractions, as will be proved in the next scholium.
COROLLARY I.
- A body by two forces conjoined will describe the diagonal of a parallelogram, in the same time that it would describe the sides, by those forces apart.
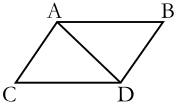
If a body in a given time, by the force M impressed apart in the place A, should with an uniform motion be carried from A to B; and by the force N impressed apart in the same place, should be carried from A to C; complete the parallelogram ABCD, and, by both forces acting together, it will in the same time be carried in the diagonal from A to D. For since the force N acts in the direction of the line AC, parallel to BD, this force (by the second law) will not at all alter the velocity generated by the other force M, by which the body is carried towards the line BD. The body therefore will arrive at the line BD in the same time, whether the force N be impressed or not; and therefore at the end of that time it will be found somewhere in the line BD. By the same argument, at the end of the same time it will be found somewhere in the line CD. Therefore it will be found in the point D, where both lines meet. But it will move in a right line from A to D, by Law I.
COROLLARY II.
- And hence is explained the composition of any one direct force AD, out of any two oblique forces AC and CD; and, on the contrary, the resolution of any one direct force AD into two oblique forces AC and CD: which composition and resolution are abundantly confirmed from mechanics.
As if the unequal radii OM and ON drawn from the centre O of any wheel, should sustain the weights A and P by the cords MA and NP; and the forces of those weights to move the wheel were required. Through the centre O draw the right line KOL, meeting the cords perpendicularly in K and L; and from the centre O, with OL the greater of the distances

