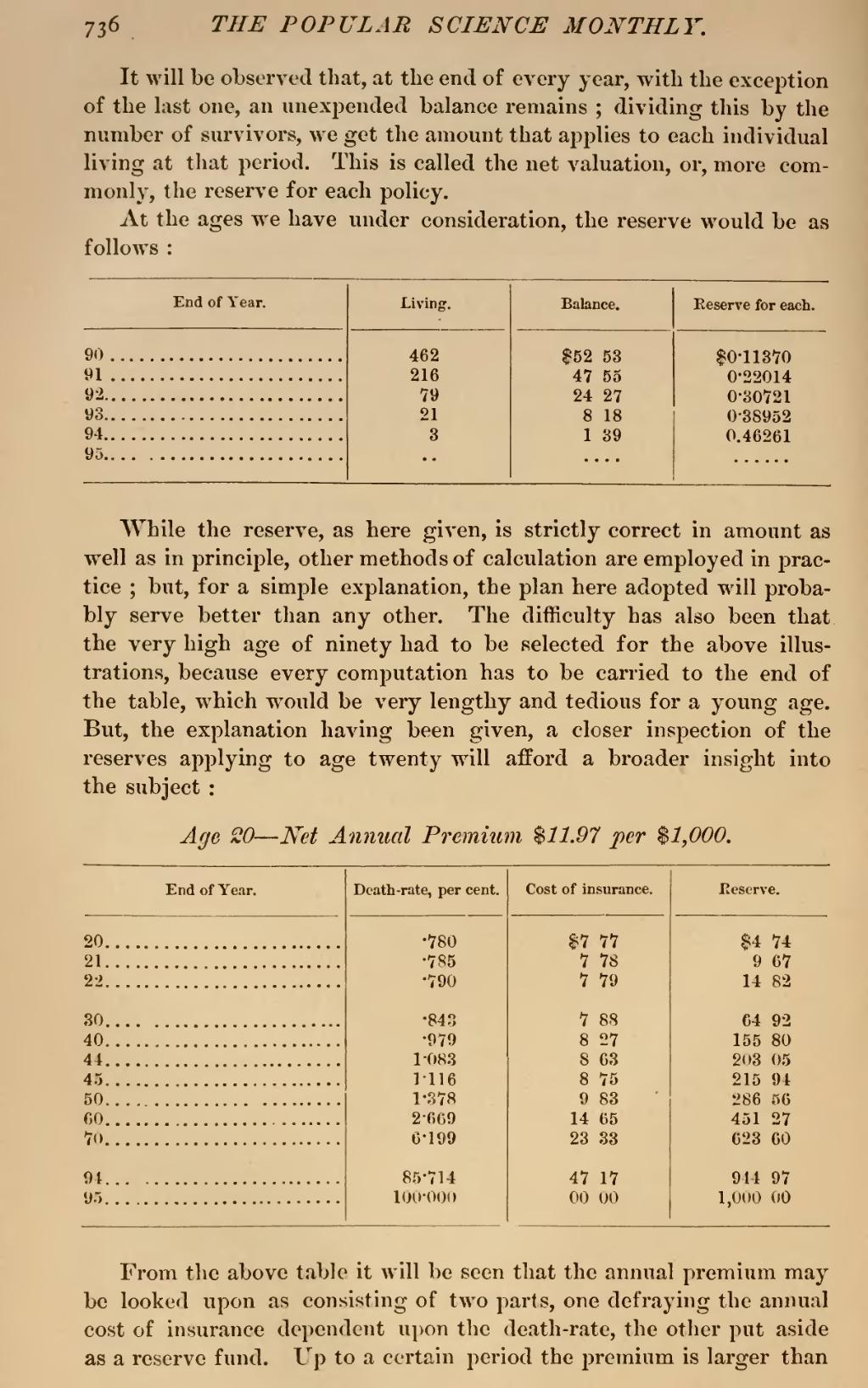
It will be observed that, at the end of every year, with the exception of the last one, an unexpended balance remains; dividing this by the number of survivors, we get the amount that applies to each individual living at that period. This is called the net valuation, or, more commonly, the reserve for each policy.
At the ages we have under consideration, the reserve would be as follows:
| End of Year. | Living. | Balance. | Reserve for each. |
| 90 | 462 | $52 53 | $0·11370 |
| 91 | 216 | 47 55 | 0·22014 |
| 92 | 79 | 24 27 | 0·30721 |
| 93 | 21 | 8 18 | 0·38952 |
| 94 | 3 | 1 39 | 0.46261 |
| 95 | . . | . . . . | . . . . . |
While the reserve, as here given, is strictly correct in amount as well as in principle, other methods of calculation are employed in practice; but, for a simple explanation, the plan here adopted will probably serve better than any other. The difficulty has also been that the very high age of ninety had to be selected for the above illustrations, because every computation has to be carried to the end of the table, which would be very lengthy and tedious for a young age. But, the explanation having been given, a closer inspection of the reserves applying to age twenty will afford a broader insight into the subject:
Age 20—Net Annual Premium $11.97 per $1,000.
| End of Year. | Death-rate, per cent. | Cost of insurance. | Reserve. |
| 20 | ·780 | $7 77 | $4 74 |
| 21 | ·785 | 7 78 | 9 67 |
| 22 | ·790 | 7 79 | 14 82 |
| 30 | ·843 | 7 88 | 64 92 |
| 40 | ·979 | 8 27 | 155 80 |
| 44 | 1·083 | 8 63 | 203 05 |
| 45 | 1·116 | 8 75 | 215 94 |
| 50 | 1·378 | 9 83 | 286 56 |
| 60 | 2·669 | 14 65 | 451 27 |
| 70 | 6·199 | 23 33 | 623 60 |
| 94 | 85·714 | 47 17 | 944 97 |
| 95 | 100·000 | 00 00 | 1,000 00 |
From the above table it will be seen that the annual premium may be looked upon as consisting of two parts, one defraying the annual cost of insurance dependent upon the death-rate, the other put aside as a reserve fund. Up to a certain period the premium is larger than