Project Longshot/Appendix

←

Spacecraft Design

Project Longshot

Appendix

→

1312384Project Longshot — Appendix

APPENDIX

Delta-V Calculations

Assumptions:

space station orbit altitude = 300 km
space station orbit inclination = 28.5 deg
obliquity = 23.5 deg
1 AU = 149.6 x 10⁶ km
Earth radius = 6378 km
f_earth = GM_e = 398,601.2 km²/sec²
f_sun = GM_e = 1.3271544 x 10¹¹ km²/sec²
f_Jupiter = GM_e = 1.268 x 10⁸ km²/sec²

(1) Velocity of probe about the earth:

V_p = (GMe/Rcircular).5 = (398,601.2/6678)^.5 = 7.7258 km/sec

(2) Amount of plane change:

i = 61x − (28.5x + 23.5x) = 9x

(3) Delta-V for 9x plane change:

Delta-V_pc = 2 x V_p x sin(i/2) = 1.2123 km/sec

(4) Earth escape velocity:

V_e−escape = (2GMe/R)^.5 = 10.9260 km/sec

(5) Delta-V to escape earth:

Delta-V_e−esc = V_e−esc - V_p = 3.2002 km/sec

(6) Velocity of probe around sun:

V_p−sun = (f_sun/1 AU).5 = 29.7849 km/sec

(7) Solar system escape velocity:

V_sun−escape = (2f_sun/1 AU)^.5 = 42.1221 km/sec

(8) Delta-V to escape the solar system:

Delta-V_sun−esc = V_sun−esc - V_p−sun = 12.4273 km/sec

(9) Total Delta-V required to escape solar system:

Delta-V_total = 16.8398 km/sec

Rough calculations for Delta-V's for orbit changes to take the probe out to Jupiter (to take on fuel) are made using Hohmann transfer equations as an approximation (actual orbits would be patched-conics). The first six calculations are the same for this analysis:

(1) Energy of Hohmann transfer orbit:

E_t = −f_sun/6.2 AU = −143.0894 km²/sec²

(2) Perigee velocity of transfer orbit:

V₁ = [2(f_sun/1 AU + E_t)]^.5 = 38.6171 km/sec

(3) Delta-V to enter transfer orbit:

Delta-V₁ = V₁ − V_p−sun = 8.8223 km/sec

(4) Apogee velocity of transfer orbit:

V₂ = [2(f_sun/5.2 AU + E_t)] = 7.4157 km/sec

(5) Velocity required to orbit Jupiter at an altitude of 500,000 km:

V₃ = (f_Jupiter/571370)^.5 = 14.8971 km/sec

(6) Delta-V to inject into orbit about Jupiter:

V₃ − V₂ = 7.4814 km/sec

(7) Jupiter escape velocity:

V_3−escape = (2f_Jupiter/571370)^.5 = 21.0676 km/sec

(8) Delta-V to escape Jupiter:

Delta-V_3−esc = V_J−esc − V_J = 6.1705 km/sec

(9) Velocity of probe about sun at Jupiter distance:

V_p−sun−J = (f_sun/5.2 AU)^.5 = 13.0601 km/sec

(10) Velocity to escape sun at Jupiter distance:

V_{sun−esc−J} = (2f_sun/5.2 AU)^.5 = 18.4697 km/sec

(11) Delta-V to escape sun at Jupiter distance:

V_{sun−esc−J} - V_p−sun−J = 5.4087 km/sec

(12) Total Delta-V for Jupiter analysis Delta-V

V_total = 32.2954 km/sec

This is nearly twice the Delta-V required for the first case. This fact, along with the difficulties involved in mining the atmosphere of Jupiter, getting the fuel to a million kilometer orbit around the planet, etc., has made it obvious that obtaining fuel from Jupiter is not feasible.

Acceleration and Velocity Profiles

1. Accelerations. The accelerations for the mission were found using the equation F=ma. Since it is a constant thrust, the acceleration will increase at a constant rate. The acceleration was found by dividing the thrust by the mass left at the time. This gives the acceleration chart on page.

2. Velocity. Since the acceleration changed at such a small rate, it was assumed that an average value for the acceleration could be used for computing the velocity. The acceleration at the beginning of a phase and at the end of a phase were averaged. This acceleration was then multiplied by the time interval for which it pertained. This delta V was then added to the previous velocity. The turning point for the mission was found with the computer program on the next page. Different turning points were tried until one was found that gave a final velocity of about 32.935 km/s.

DESII 07 Apr 88 17:23

100 REM *** THIS PROGRAM ASSUMES THAT THE ACCELERATIONS***
110 REM *** CAN BE AVERAGED SINCE THEIR VALUE IS SMALL***
120 REM ** AND THEY DO NOT CHANGE MUCH.***
130 REM
140 PRINT "ENTER THE TURNING POINT."
150 INPUT TP
160 LET A1A=(.00464+.00577)/2
170 LET V/A1A*33.35*3147E7
180 REM
190 REM *** VELOCITY AT RELEASE OF TANKS 1 AND 2 ****
200 REM
210 LET A2A=(.00619+.0084)/2
220 LET V=V+A2A*33.35*3.147E7
230 REM
240 REM **** VELOCITY AT RELEASE OF TANKS 3 AND 4 ****
250 REM
260 LET A3A=(.00931+ATP)/2
270 LET V=V+A3A*(TP-66.7)*3.147E7
280 REM
290 REM ****VELOCITY AT TURNING POINT ****
300 REM
310 LET A4A=(.021+ATP)/2
320 LET V=V-A4A*(100.05-TP)*3.147E7
330 REM
340 REM **** FINAL VELOCITY ****
350 REM
360 PRINT V/1000, ATP
370 PRINT "GO AGAIN?"
380 INPUT ZZ$
390 IF ZZ$="Y" THEN 150
400 END

Ready

Probe Wt.	No. SRB's Shuttle Size	Delta V	S/C TOTAL Wt.
mt		km/s	mt
1409.695	.1	.205	1469.3
1409.695	.2	.401	1528.905
1409.695	.3	.589	1588.51
1409.695	.4	.768	1648.115
1409.695	.5	.94	1707.72
1409.695	.6	1.104	1767.325
1409.695	.7	1.263	1826.93
1409.695	.8	1.415	1886.535
1409.695	.9	1.562	1946.14
1409.695	1	1.703	2005.745

Plane change of 9 degrees
Delta V required is 1.2123 km/s

Probe Wt.	No. SRB's Shuttle Size	Delta V	S/C TOTAL Wt.
mt		km/s	mt
694.435	1	2.914	1280.485
694.435	1.1	3.112	1350.09
694.435	1.2	3.298	1409.695
694.435	1.3	3.475	1469.3
694.435	1.4	3.643	1528.905
694.435	1.5	3.802	1588.51

Escaping Earth
Delta V required is 3.2002 km/s

Probe Wt.	No. SRB's Shuttle Size	Delta V	S/C TOTAL Wt.
mt		km/s	mt
396.41	.1	.689	456.015
396.41	.2	1.28	515.62
396.41	.3	1.795	575.225
396.41	.4	2.249	634.83
396.41	.5	2.653	694.435

Aiding in escaping solar system
Delta V required is at least 2.5 km/s

Laser-Pumped Light Sail

Assumptions:

1) 100% of laser is focused onto the sail continuously for one year.

2) the solar energy to pressure ratio holds true for the specific laser used.

At 1 A.U.:

1353 watts/square meter from the sun

and

4.6E-6 N/square meter from the sun

therefore,

2.94E8 watts/N.

Payload Mass = 30,000 kg

Delta V required = 13500 km/sec

Time interval = 31,472,262 sec (1 year)

Therefore,

Required acceleration = .429 m/sec squared

and

The force required = 1268.8 N

So that with a laser operating at 100% efficiency

Required power = 3.78E12 watts

EXTREME HIGH TEMPERATURE EXPANSION OF GAS

"Ideal" Rocket Nozzle: Perfect Gas

Steady Flow - no shock, friction or heat losses

One Dimensional Flow

Frozen Chemical Equilibrium

V_e (exit velocity) = L E

L = Limiting Gas Velocity

E = Pressure Expansion Ratio

E={\sqrt {1-{\frac {P_{e}}{P_{t}}}^{\frac {\gamma -1}{\gamma }}}}\quad \quad (P_{e}=0)

L={\sqrt {\frac {2\gamma {\overline {R}}T_{t}}{(gamma-1)M}}}

\gamma _{(monoatomic)}=1.67

{\overline {R}}=8.31441

M_{H_{1}}=1.00794

T_{t_{critical\,deuterium\,fusion}}=3.5x10^{8}\,\,\,K

L_{\mathrm {max} }=379{\frac {km}{sec}}

I_{sp}={\frac {V_{e}}{g}}=39000\,\mathrm {sec}

Fusion Reaction

\mathrm {He_{3}+H_{2}\rightharpoonup He_{4}+H_{1}}

at reaction temperature:

{\begin{alignedat}{2}\mathrm {He_{4}} &=\mathrm {\alpha _{4}^{2+}+2e^{-}} \\\mathrm {H_{1}} &=\mathrm {p_{1}^{+}+e^{-}} \\\end{alignedat}}

the resulting charged particles can be magnetically funneled and used to charge induction coils upon exiting.

Pellet Size vs. Frequency

an engineering analysis must be done on the proposed engine to determine pellet size and pulse frequency.

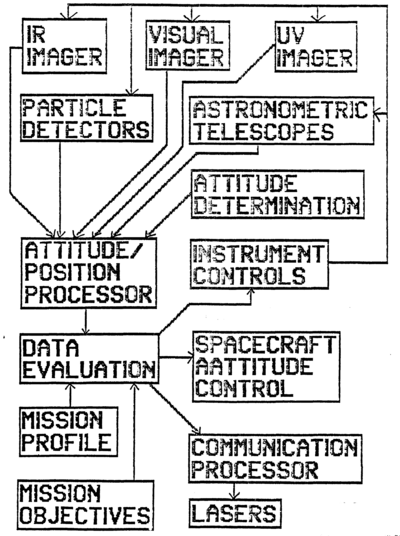
PROCESSING BLOCK DIAGRAM

alt=IR IMAGER VISUAL IMAGER UV IMAGER PARTICLE DETECTORS ASTRONOMETRIC TELESCOPES ATTITUDE DETERMINATION ATTITUDE / POSITION PROCESSOR INSTRUMENT CONTROLS DATA EVALUATION SPACECRAFT ATTITUDE CONTROL MISSION PROFILE COMMUNICATION PROCESSOR MISSION OBJECTIVES LASERS

Sizing of the Fuel Tanks

1. Tank Volume

The storage density for the fuel is .0708 tons per cubic meter. Therefore, the total volume needed is:

Vol	= (264.276 mt)*(1/.0708 mt/m^3)
	= 3732.71 m^3

The radius of the fuel tanks is set at 2.5 meters and the length is then computed.

length	= (Vol/6)/(pi*r^2)
	= (3732.71 m^3/6) / (pi*(2.5)^2)		= 31.68 meters

The total volume is divided by six, because six fuel tanks are used.

2. Tank Thickness

A. Interstellar cruise phase

Newton's equation, F=ma, is used to find the forces on the fuel tanks during flight. The maximum force will occur when the acceleration is a maximum. This is when the mass is a minimum for a constant thrust problem. In our case, the minimum mass is:

Mmin	= 2 fuel tanks + 6 straps + center section + engine + payload
	= 89.345 metric tons

Therefore,

Amax	= Thrust/m
	= 1.838e3 N / 89.345e3 kg
	= .021 m/s^2

The maximum force possible on the tanks could then be:

Fmax	= (mass of fuel in tanks) * a
	= 44.05e3 kg * .021 m/s^2
	= 924.97 N

A safety factor of 5 is now applied to find the design load.

Fdes	= 5 * F
	= 4.62 kN

Next, the tank area that the force is acting on is found.

Area	= pi * r^2
	= pi * 2.5^2
	= 19.635 m^27

So, the pressure will be:

p	=F/A
	= 4.62 kN / 19.635 m^2
	= 235.54 N/m^2

The thickness of the tanks is now determined.

t = (P * r) / (2 * yield stress)

If we assume that we will use A1 1100-0, the yield stress is 3.45e7 N/m^2. This gives a thickness of:

t	= (235.54 N/m^22.5 m)/(23.45e7 N/m^2)
	= 8.53e-6 m or .00853 mm

Therefore, the fuel tanks can be made from 2 mm A1 1100-0 sheets.

B. Orbital Maneuvers

Since the upper stages will require advanced upper stages, the forces on the spacecraft are not known. Through the use of staging, multiple burns per maneuver, and the use of a stronger aluminum alloy, the thickness of the fuel tanks can be kept at 2 mm.

WEIGHT TABLE

Item	Components	Weight Metric Tons
Engine
	Chamber	4.35
	Igniter	17.543
	Field Coil	10.245
	Total	32.138
Fuel	Total	264.276
Structure
	Fuel Tanks	55.038
	Straps	9.151
	Center Section	1.737
	Other Structure	4.074
	Total	70.00
Payload
	Reactor	10.00
	Instruments	3.00
	Lasers	2.00
	Misc. (shielding, etc...)	15.00
	Total	30.00

	Overall Total	396.414