Steam Heating and Ventilation/Chapter IV
Chapter IV.—Indirect Radiators.
The preceding chapter comprised mainly a discussion of the principles involved in the action of radiators in giving out their heat to the air and objects surrounding, but was confined almost entirely to direct radiation. Many of the deductions as to the relative value of different kinds of surface may be applied to indirect radiators as well, but a theoretical discussion of the latter requires some entirely different considerations from those presented in the last chapter on direct radiation. The indirect radiator is located below and outside of the room to be heated; it is enclosed by a casing, which has an air connection to the outside of the building, and a hot-air flue to the room to be heated. In this discussion it should be stated that the term indirect radiation is often applied to radiators or heating coils which are used in connection with a fan which creates a forced draft. In the author's opinion this is a mistake, as the element of forced draft involves still other considerations, and such radiators are merely heating coils for mechanical ventilation and should be discussed separately as such. The indirect radiator proper depends entirely upon the draft action of the heated column of air above it for its ventilating effect, and also for a means of communicating its heat to the room above.
Theory of indirect radiator.—The theory of the indirect radiator may be illustrated by the accompanying Figure 26, in which is the radiator set in a box, , and provided with a cold-air connection, , to the outside air (generally having a damper, ), and a hot-air duct, , to the room to be heated, with a register, , in the floor or wall of the room. Steam is supplied to the radiator by the pipe, , through the casing. The heat of the radiator causes a column of hot air to rise through , and the current is maintained by the excess of pressure of the column of cold air outside over that of the column of hot air in . The exact pressure which creates this current is found in the excess weight of a column of cold air of height over that of a column of the same height and of the temperature of the air in .
This may be calculated as follows, since the weight of a cubic foot of a gas of any temperature is inversely proportional to its absolute temperature, which is the temperature in degrees Fahrenheit + 460, or , where is the weight per cubic foot, the temperature in degrees Fahrenheit, and a constant, different for each gas and which, for air, equals approximately 40. If t be the temperature of the cold air and be that of the air in , then the pressure per square foot due to a column of cold air of height feet would be and the pressure due to a column of hot air of the same height would be . The difference of pressure which creates the flow of air then is
The head, , which creates the velocity of flow, is equal to the height of a column of air of temperature which would give the pressure , or
By the laws governing the flow of fluids the theoretical velocity with which the current of air would move through is where is, as above, the head producing the flow. This would be the velocity produced in by the difference in pressure were it not for the resistance to the flow caused by the friction of the air in passing through the radiator and ducts and past dampers, registers, etc. This resistance often reduces the velocity to less than half of the theoretical velocity. Mr. Alfred E. Wolff, however, recommends that 50 per cent. of the theoretical velocity be taken in the case of ventilating flues which depend on a heated column for their action.
The practical application of this theory is, however, one of considerable difficulty. In an indirect radiator in a given situation we do not know the temperature of the heated column, and, what is most important, we do not know the resistance of the air passages. What we do know is that we have a radiator of so many square feet surface located in a certain system of boxing, ducts, etc., and supplied with steam, or hot water, at a certain temperature. The temperature of the air outside being also known, or assumed for extreme conditions, the question is how much air will be delivered by this radiator to the room and also to what degree it will be heated.
The amount of heat given off to the air depends upon the velocity and upon the difference between the temperature of the steam in the radiator and the mean temperature of the air around it; and the velocity depends, again, upon the difference of temperature between the entering and out-going air as well as upon the air resistance as embodied in the arrangement of ducts, structure of radiator, etc. All of these make a complicated system of variables which it is impossible to apply in theoretical formulas and anticipate what the actual result will be. In practice, a given radiator in a given setting, and with given temperatures of steam and outside air, condition of wind being constant, will deliver a definite amount of air heated to a definite degree and the velocity and final temperature adjust themselves until there is an equality between the temperature head acquired and the velocity head plus the head necessary to overcome the resistance. But exactly how this combination will adjust itself it is wellnigh impossible to say beforehand, inasmuch as the air resistance is a quantity very difficult to predetermine, it being very greatly affected by a slight change in the arrangement. Mills' test of indirect radiators.—For these reasons, all rules thus far deduced for installing indirect radiators are entirely empirical. But very few tests have been made upon indirect radiators with a view to establishing the relation between any of the variables involved; but some valuable results might be obtained by a thorough series of experiments carefully and systematically carried out. Mr. J. H. Mills, in his work on Heat, published in 1883, presents the collected results of a number of tests on several indirect radiators of different types. These tests were made on various radiators at various times and by several different experimenters.
The writer has taken from the Mills table the results given for the two radiators upon which the greater number of tests were made and has endeavored by plotting some diagrams from them to determine something of the relationships between the existing variables. The results published by Mr. Mills on the Gold pin radiator and the Whittier radiator are presented in the
| Tests on Gold's Pin Indirect Radiator. | ||||||||||
| Temperatures. | Diff. Temp. | |||||||||
| Experimenter. | Date. | Sq. ft. of Radiation. | Steam. | Entering Air. | Exit Air. | Enter'g and Exit Air. | Steam and Enter'g Air. | Oz. Water Condensed per sq. ft. per hr. | Air. Cu. ft. per sq. ft. per hr. | B. T. U. per sq. ft. per hr. |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 160 | 160 | 215 | 5.44 | 111 | 340 |
| W. J. Baldwin | 1875 | 60 | 239 | 71 | 168 | 97 | 168 | 3.83 | 128 | 239 |
| W. Warner | 1880 | 70 | 222 | 42 | 145 | 103 | 180 | 4.60 | 145 | 288 |
| Dr. Gray | 1875 | 90 | 259 | 33 | 125 | 92 | 226 | 6.54 | 231 | 400 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 129 | 129 | 215 | 9.15 | 214 | 572 |
| J. R. Reed | 1875 | 58 | 222 | 52 | 127 | 75 | 170 | 7.92 | 343 | 495 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 129 | 129 | 215 | 12.65 | 319 | 791 |
| J. H. Mills | 1876 | 76 | 239 | 81 | 159 | 78 | 158 | 8.49 | 354 | 531 |
| W. J. Baldwin | 1885 | 60 | 227 | 82 | 150 | 68 | 145 | 8.16 | 390 | 510 |
| J. H. Mills | 1876 | 76 | 239 | 90 | 158 | 67 | 148 | 8.91 | 433 | 558 |
| W. J. Baldwin | 1885 | 60 | 227 | 70 | 137 | 67 | 158 | 8.93 | 433 | 558 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 121 | 121 | 215 | 15.92 | 428 | 995 |
| J. H. Mills | 1876 | 77 | 230 | 88 | 158 | 70 | 142 | 10.04 | 467 | 628 |
| J. H. Mills | 1876 | 76 | 259 | 90 | 166 | 76 | 169 | 15.16 | 649 | 948 |
| J. H. Mills | 1876 | 76 | 222 | 90 | 145 | 51 | 132 | 12.58 | 741 | 784 |
| J. H. Mills | 1876 | 77 | 227 | 94 | 145 | 51 | 133 | 13.43 | 855 | 839 |
| Tests on G. Wittier's Indirect Radiator | ||||||||||
| C. B. Richards | 1873-4 | .. | 215 | 0 | 135 | 135 | 215 | 4.40 | 106 | 275 |
| J. R. Reed | 1875 | 68 | 222 | 45 | 129 | 84 | 177 | 5.09 | 197 | 318 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 102 | 102 | 215 | 6.66 | 212 | 416 |
| J. R. Reed | 1875 | 68 | 222 | 52 | 110 | 58 | 170 | 5.50 | 308 | 344 |
| J. R.- Reed | 1875 | .. | 222 | 52 | 114 | 62 | 170 | 5.86 | 307 | 366 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 87 | 87 | 215 | 8.53 | 319 | 533 |
| C. B. Richards | 1873-4 | .. | 215 | 0 | 77 | 77 | 215 | 10.14 | 428 | 634 |
On the diagram of the tests of the Gold pin radiator are plotted the curves representing the relation for a difference of temperature of 215 degrees Fahr., and also approximately that for a difference of 150 or 160 degrees. On the diagram for the Whittier radiator are plotted only the curve for tests at a difference of temperature of 215 degrees. There are some points, which are marked by a cross on the diagram, that seem to be decidedly out of place; that is, for the difference of temperature the ratio between the British thermal units per square foot and the cubic feet of air per square foot is too low. Considering the fact, however, that the tests under discussion were made on radiators of different sizes, and several years apart, by different men, and under very different conditions of setting, the uniformity of the curves is very striking, and the few points which are evidently out of place are doubtless due either to some error of observation or in some marked difference in the way of taking measurements.
Inasmuch as in practice we are most concerned with extreme conditions, the curves for the difference of temperature of 215 degrees are of most value, as they may be taken to represent an initial air temperature of 0 degree and low-pressure steam at 215 degrees. It will be noticed that the 215-degree curve for the Gold pin radiator is quite different from that for the Whittier. As these curves show for a constant difference of temperature, the relation between the cubic feet of air per square foot of radiator, which is a measure of the velocity of air flow, and the heat given off per square foot, they take into consideration all variations in setting; and the similar curves for any two radiators indicate precisely the relative values of the two radiators. For example, the 215-degree curve of the Gold pin radiator shows a uniformly higher ratio between the British thermal units per square foot and the cubic feet of air per square foot than the similar curve of the Whittier. The former is, by just so much, therefore, the more effective radiator. Mr. Mills states of the Gold pin radiator, which was first introduced by Mr. Samuel Gold in 1862, that it "has proved the most efficient indirect-heating surface ever produced." It is still extensively used, although some modern makes are largely supplanting it. It is to be regretted tests have not been made on some of the more modern types in comparison with it.
If it is desired to consider this question mathematically, the equation of the 215-degree curve of the Gold pin radiator is approximately , whereas the equation of the similar curve of the Whittier radiator is , in which H represents the British thermal units per square foot and A the cubic feet of air per square foot. In other words, with the Gold pin radiator the heat is proportional to the 79/100 power of the number of cubic feet of air per square foot of radiation (nearly equal to the fourth root of the cube), while with the Whittier it is proportional to the 0.68 power (nearly the cube root of the square); and the nearer this exponent approaches unity the more effective will the radiator be, unless there is a large variation in the coefficient.
As yet there is not very much practical data on indirect radiators. It would be of special value if some tests were made of the more modern forms of indirects to establish corresponding diagrams for them. Such tests should be made preferably in cold weather and with a constant difference of temperature between the steam and entering air of about 215 or 220 degrees. The setting of the radiator and air ducts should approximate practical conditions and the velocity (as cubic feet of air per square foot of radiator) could be varied by changing the resistance to air flow by means of dampers. In this connection some experiments of much practical value could also be made on the air resistance by determining the velocity in cubic feet of air per square foot of radiator attained for different temperatures in the hot-air duct, D, in Figure 26.
Indirect radiators are seldom installed except for rooms on the first or second floors; and in the former case the duct, D, is very short, and in the latter it is usually from 12 to 16 feet long. It should be stated in this connection that indirects of large size should be spread out as much as possible so as to give a large area against the current of air. If they are made of several radiators, one above the other, as is sometimes the case, by the time the air reaches the upper ones it is of so high a temperature that they have but little effect in comparison with the lower section.
Direct-indirect radiators.—In regard to direct-indirect radiators, their action is much the same as that of the indirect; but they have the added effect of radiation, whereas with the indirect all heat is conveyed by convection. Furthermore, with the indirect type, the flues are much shorter and the air resistance much less than with the indirect setting. As a matter of fact, the principal air resistance with the former is due to the passage of the air through the radiator itself.
The author knows of no tests that have been made on direct-indirect radiators, but considers they would be of value if they should establish the relation between the heat given out and the air delivery per square foot of radiator for constant differences of temperature between the steam and entering air. As stated in a previous chapter, in the opinion of the author the use of the direct-indirect radiator, which has been, up to this time, and is now, very limited, will be materially increased in the immediate future, as in connection with exhaust fans they form an effective means of introducing adequate ventilation into buildings which are not very densely populated but in which there is a decided need of ventilation. This class of buildings includes especially our palatial modern office buildings and also a certain class of factories. The more extensive introduction of these radiators, as well as of the indirects, is greatly delayed by the lack of accurate information as to what the different makes on the market will do in the way of heating under various practical conditions of temperature and setting. There seems, therefore, to be a considerable field for investigation in this regard.
Circulation in radiators.—In the preceding chapter, and thus far in this one, we have discussed the action of radiators in doing the work they are intended for, and have pointed out the theoretical and practical considerations involved. Before discussing the bearing of these principles upon the design of a heating plant it is necessary to turn the attention to another consideration involved in the action of radiators, and one which is of much importance in the practical efficiency of a heating plant. This is the circulation of steam within the radiator.
Any one who has had even a slight experience with radiators well knows the troubles that arise on account of dripping air valves, water-hammer, and the pocketing of air, and other evils that are due to imperfect steam circulation. While evils of this kind are frequently attributable to imperfect circulation in the piping, yet there is a great difference in the operation of radiators in this respect.
As shown in a previous chapter, any heating system contains a considerable amount of air, and it is necessary to provide means for venting the piping and radiators so as to allow it to escape in the proper way. Ordinarily, when steam is shut off from a radiator it fills with air at atmospheric pressure, through the air valve; and when steam is turned on, this air must in some way be allowed to escape before all of the surface can have full heating effect. The rapidity with which the air will be displaced by the steam depends on where the air valve is placed and on the design of the radiator. In some radiators the air will flow out the air valve and be followed up by the steam rapidly and uniformly; while in others the air will pocket in places, and it may be hours before it all works out. The action of radiators in this regard is very peculiar, and it is frequently exceedingly difficult to predict beforehand whether or not a radiator will allow good circulation.
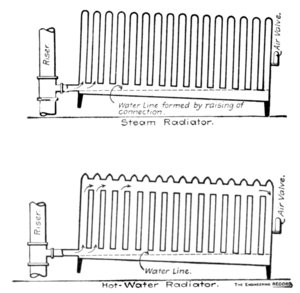
As a general thing the simplest radiators are the most effective. Air is heavier than steam of the same pressure, but in a heating system the air will always find its way to the dead end, or point where there is no circulation. If a straight, vertical pipe, closed at the top, be connected to a source of steam supply, any air in the system will accumulate at its top. If steam is turned on an ordinary two-column steam radiator which is full of air and has a tight air valve, after some moments the first few loops will become filled with steam and perfectly hot, the remaining loops being full of air and cold. If the radiator has a two-pipe connection the air may work out to some extent through the return; but if it has only a one-pipe connection it will remain in this condition as long as the air valve is kept closed. If, however, the radiator be of the hot-water type—that is, it has its loops connected by openings through the top as well as at the bottom—the steam will run along the top of the radiator, and as long as the air valve is closed it will remain hot across the top and the lower part of the loops will be cold, with the possible exception of the two end ones. If now the air valves be opened, the air will flow uniformly from the regular steam type, the steam filling one loop after another; but with the hot-water type, as soon as the air valve is opened the steam will flow first across the top, then across the bottom, and the air will gradually work out, first from the loops near the air valve. This will serve to illustrate to some extent the action of air in radiators.
Circulation in direct radiators.—As regards direct radiators, the ordinary two-column steam type gives the most perfect circulation. When steam is turned on it compresses the air to the pressure of the steam, and immediately fills a portion of the bottom and the nearest loops to the inlet. Each loop then acts independently and the air syphons out of each, one after another, until all are full of steam. In the hot-water type, as shown, the steam has a free circulation around the radiator as a whole, which interferes with the air circulation in each loop, so that these radiators will often remain air bound in the center for a considerable length of time. In the same way three and four-column radiators will become air bound in the middle columns, the air syphoning out of the two outside columns and establishing a circulation there, while the contents of the inner columns remain quiet. In this connection it should be stated that a strictly one-column radiator would not allow circulation at all, or but very slowly, but the so-called one-column radiators are practically two columns, as they are cast with a partition running up the loop with an opening at its top. Radiators of the flue pattern always have one or two similar partitions. Direct radiators which are low and wide are almost universally built with the loop opening in the top as well as the bottom, under the impression that otherwise the outside portions of the loops would easily become air bound. Some of the author's experiences, however, lead him to think that as far as this is concerned the circulation in this type also is better without the top connection. There is, however, one practical advantage which the top-connection radiators have over the steam type, that is more especially marked in long, low radiators. If, with a one-pipe connection, the supply end is somewhat raised, on account of bad steam fitting, the unwarranted expansion of a riser, or other cause, it may trap the end loops of the steam type so as to shut off the air valve entirely, whereas the top-connection type would have a circulation in any such case, as is illustrated in Figure 29. Such a condition, though the result either of poor design or bad workmanship, is still a frequent occurrence in practice.
Circulation in indirect radiators.—Indirect radiators, which are always made to lie horizontal, are usually made with loops equivalent to the two-column form, but of greatly exaggerated width and very low, and have the steam connection at one of the lower corners. There are, however, some special forms, and one has to use his judgment as to their qualities in respect to circulation.
It is important that radiators be built and set so that but little, if any, water will stand in them. The openings for pipe connections should be at the lowest point and the radiator should drain perfectly. The loops of some radiators are built so that there is quite a pocket under the opening. This should be avoided, as the water which stands in them, and is allowed to become cold, is a fertile cause of water-hammer as well as dripping air valves. When the steam is turned into the cold radiator it is apt to gather up this water, together with the freshly condensed water, and drive it into the back end, clogging up the passages and causing water-hammer and dripping air valves, to the great discomfort of those in proximity.
Air valves.—In regard to air valves there is but little to be said. They are a necessity to every radiator; without them any radiator would soon become dead by being filled with air. Automatic air valves have almost entirely superseded the old-time hand air valves. They are made with a composition disc, with a high coefficient of expansion, which is arranged to close the valve as soon as the hot steam comes in contact with it. They are also provided with a screw attachment by which the valve opening can be adjusted after the valves are in place. The disadvantage of the automatic air valve is that when steam is turned on, the entire radiator will become heated. For this reason the author prefers the plain hand air valve on radiators in his own rooms, as the amount of the radiator heated can be very accurately regulated by means of them, especially when they are connected on a one-pipe system. The automatic air valve, however, takes the circulation in the radiator entirely out of the hands of persons who are not acquainted with their principles, and in the case of indirects is a necessity.
Air valves are generally placed about 18 inches from the bottom of the last loop. Theoretically the best location would be near the bottom of this loop, but if there is danger of much water in the radiator they are safer near the top. The author has cured several cases of a dripping air valve by tapping it into the extreme top of the loop. When so placed the last loop will sometimes remain partially air bound on one side, but otherwise they are quite effective in this position. The trouble referred to, however, is much more often due to improper piping than to anything in the design of the radiator.
- ↑ Mr. Mills gives a diagram somewhat similar to these, but the author cannot find that the points given are taken directly from the tests which he produces.