A Dictionary of Music and Musicians/Resultant Tones

by James Lecky

RESULTANT TONES (Fr. Sons résultans; Ger. Combinationstöne) are produced when any two loud and sustained musical sounds are heard at the same time. There are two kinds of resultant tones, the Differential and the Summational. The 'Differential tone' is so called because its number of vibrations is equal to the difference between those of the generating sounds. The 'Summational tone' is so called because its number of vibrations is equal to the sum of those of the generating sounds. The following diagram shows the pitches of the differential tones of the principal consonant intervals when in perfect tune.

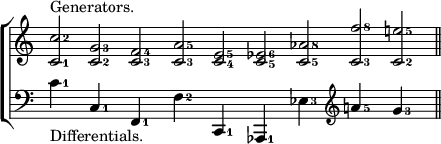
If the interval be wider than an octave, as in the last two examples, the differential is intermediate between the sounds which produce it. These tones can be easily heard on the ordinary harmonium, and also on the organ. They are not so distinct on the piano, because the sounds of this instrument are not sustained. By practice, however, the resultant tones can be distinguished on the piano also.

Dissonant as well as consonant intervals produce resultant tones. Taking the minor Seventh in its three possible forms the differentials are as follows:—

The 1st form of minor Seventh is obtained by tuning two Fifths upwards (C-G-D) and then a major Third downwards (D-(Music characters)B♭): its differential tone is (Music characters)A♭, an exact major Third below C. The 2nd form is got by two exact Fourths upwards (C-F-B♭): the differential is then (Music characters)A♭, which is flatter than the previous (Music characters)A♭ by the interval 35 : 36. The 3rd form is the so-called Harmonic Seventh on C, whose differential is G, an exact Fourth below C. The marks (Music characters), (Music characters), here used to distinguish notes which are confused in the ordinary notation, will be found explained under Temperament.

Hitherto we have spoken only of the differential tones which are produced by the fundamentals or prime partial tones of musical sounds. [See Partial Tones.] But a differential may also arise from the combination of any upper partial of one sound with any partial of the other sound; or from the combination of a differential with a partial, or with another differential. Thus the major Third C-E may have the following differential tones:—

All these tones are heard simultaneously; but for convenience the differentials of the 1st, 2nd, 3rd, and 4th orders are written with notes of different length. We see, then, that the number of possible resultant tones is very great; but only those which arise from the primes of musical sounds are sufficiently strong to be of practical importance.

In enabling the ear to distinguish between consonant and dissonant intervals, the differential tones are only less important than the upper partials. Thus if the chord G-E-C be accurately tuned as 3:5:8, the differential of G-C coincides with E, and that of E-C with G. But if the intervals be tempered the differentials are thrown out of tune, and give rise to beats. These beats are very loud and harsh on the ordinary harmonium, tuned in equal temperament. Again, in the close triad C-E-G the differentials of C-E and of E-G coincide and give no beats if the intervals be in perfect tune. On a tempered instrument the result is very different. If we take C to have 264 vibrations, the tempered E has about 332½, and the tempered G about 395½ vibrations. The differential of C-E is then 68, and that of E-G 63. These two tones beat 5½ times each second, and thus render the chord to some extent dissonant.

In the minor triad, even when in just intonation, several of the resultant tones do not fit in with the notes of the chord, although they may be too far apart to beat. In the major triad, on the contrary, the resultant tones form octaves with the notes of the chord. To this difference Helmholtz attributes the less perfect consonance of the minor triad, and its obscured though not inharmonious effect.

The origin of the differential tones has been the subject of much discussion. Thomas Young held that when beats became too rapid to be distinguished by the ear, they passed into the resultant tone. This view prevailed until the publication in 1856 of Helmholtz's investigations, in which many objections to Young's theory were brought forward. To explain what these objections are, it would be necessary to treat at some length of the nature of beats, and the reader is therefore referred to the Appendix, Article Beats, for this side of the question. The new mathematical theory given by Helmholtz is too abstruse to admit of popular exposition.

It was also part of Young's theory that the differential tone was produced in the ear alone, and not in the external air. But Helmholtz found that stretched membranes and resonators responded very clearly to differentials produced by the siren or the harmonium. This he considers to prove the existence of vibrations in the external air corresponding to the differential tones. But when the two generating tones were produced by separate instruments, the differential, though powerfully audible, hardly set the resonator in vibration at all. Hence Helmholtz concludes that the differential tone is for the most part generated in the ear itself. He further points out that certain features in the construction of the ear easily permit the action of the law which he has stated. The unsymmetrical form of the drum-skin of the ear, and the loose attachment of the ossicles are, he thinks, peculiarly favourable to the production of resultant tones.

As a consequence of his theory, Helmholtz deduced a different series of resultant tones, which he calls summational tones, because their number of vibrations is the sum of those of the generators. The existence of the summational tones which Helmholtz believes he has verified experimentally, has recently been called in question by Dr. Preyer. He points out that in some intervals, as for instance, 1:2, 1:3, 1:5, there will be a partial tone present of the same pitch as the presumed summational tone, and these cases therefore prove nothing. Again, if we take 2:3, the note 5 is not necessarily a summational tone, but may be the differential of 4 and 9 which are the 2nd partial of 2 and the 3rd of 3 respectively. Dr. Preyer was unable to find any trace of the summational tones when care had been taken to exclude the upper partials. But to do this he could only use sounds of tuning-forks gently bowed, which were far too weak to produce any resultant tones in the air. The question, however, is one of theoretic interest merely.

Not only the origin, but also the discovery of differential tones has been disputed. The earliest publication of the discovery was made by a German organist named Sorge in 1745. Then came Romieu, a French savant, in 1751. Lastly, the great Italian violinist Tartini made the phenomenon the basis of his Treatise on Harmony in 1754. But Tartini explicitly claims priority in these words:—'In the year 1714, when about twenty-two years of age, he discovered this phenomenon by chance on the violin at Ancona, where many witnesses who remember the fact are still living. He communicated it at once, without reserve, to professors of the violin. He made it the fundamental rule of perfect tuning for the pupils in his school at Padua, which was commenced in 1728 and which still exists; and thus the phenomenon became known throughout Europe.'^[1]

Tartini in some cases mistook the pitch of the differential tone; but there does not appear to be any reason for taking from him the credit of the discovery which has so long been associated with his name.

[ J. L. ]

1. De Principii dell' Armenia, Padova, 1767, p. 86.