A Dictionary of Music and Musicians/Temperament
TEMPERAMENT (Fr. Tempérament; Ger. Temperatur; comp. Ital. temperare, to tune) is the name given to various methods of Tuning, in which certain of the consonant intervals, chiefly the Fifth and Major Third, are intentionally made more or less false or imperfect; that is to say, either sharper or flatter than exact consonance would require. If, on the contrary, all the consonant intervals are made perfectly smooth and pure, so as to give no Beats (see Appendix) [App. p.798 "omit the words see Appendix"], the tuning is then called Just Intonation.
When a piece of music containing much change of key is executed in just intonation, we find that the number of notes employed in each Octave is considerable, and that the difference of pitch between them is, in many cases, comparatively minute. Yet, however great the number of notes may be, and however small the intervals which separate them, all these notes can be correctly produced by the voice; as they may be derived from a few elementary intervals, namely the Octave, Fifth, Major Third, and Harmonic Seventh.[1] Instruments like the violin and the trombone are also suitable for the employment of just intonation; because, in these cases, the player can modify the pitch of each note at pleasure, being guided by his sense of key-relation. But it is otherwise with instruments whose tones are fixed, such as the pianoforte, organ, and harmonium. Here the precise pitch of each note does not depend on the player, but is settled for him beforehand by the tuner. Hence, in these instruments, the number of notes per Octave is limited, and cannot furnish all the varieties of pitch required in just intonation. A few scales may, indeed, be tuned perfectly; but if so, certain notes which belong to other scales will be missing. Compromise then becomes a mechanical necessity; and it is found that by putting most of the consonant intervals, except the Octave, slightly out of tune, the number of notes required in modulation may be considerably reduced, without too much offence to the ear. This mode of tuning is called Temperament, and is now usually applied to all instruments with fixed tones. And although voices, violins, and trombones naturally have no need of temperament, they must all conform to the intonation of any tempered instrument which is played in concert with them.
We shall omit from the present article all reference to the arithmetical treatment of temperament, and simply deal with its physical and audible effects. We shall describe the means by which any student may obtain for himself a practical knowledge of the subject, and point out some of the conclusions to which such knowledge will probably lead him.[2] The first and most important thing is to learn by experience the effect of temperament on the quality of musical chords. To carry out this study properly it is necessary to have an instrument which is capable of producing all the combinations of notes used in harmony, of sustaining the sound as long as may be desired, and of distinguishing clearly between just and tempered intonation. These conditions are not fulfilled by the pianoforte; for, owing to the soft quality of its tones, and the quickness with which they die away, it does not make the effects of temperament acutely felt. The organ is more useful for the purpose, since its full and sustained tones, especially in the reed stops, enable the ear to perceive differences of tuning with greater facility. The harmonium is superior even to the organ for illustrating errors of intonation, being less troublesome to tune and less liable to alter in pitch from variation of temperature or lapse of time.
By playing a few chords on an ordinary harmonium and listening carefully to the effect, the student will perceive that in the usual mode of tuning, called Equal Temperament, only one consonant interval has a smooth and continuous sound, namely the Octave. All the others are interrupted by beats, that is to say, by regularly recurring throbs or pulsations, which mark the deviation from exact consonance. For example, the Fifth and Fourth, as at (x), are each made to give about one beat per second. This error is so slight as to be hardly worth notice, but in the Thirds and Sixths the case is very different. The Major Third, as at (y), gives nearly twelve beats per second: these are rather strong and distinct, and become still harsher if the interval is extended to a Tenth or a Seventeenth. The Major Sixth, as at (z), gives about ten beats per second, which are so violent, that this interval in its tempered form barely escapes being reckoned as a dissonance.

The Difference-Tones resulting from these tempered chords are also thrown very much out of tune, and, even when too far apart to beat, still produce a disagreeable effect, especially on the organ and the harmonium. [Resultant Tones.] The degree of harshness arising from this source varies with the distribution of the notes; the worst results being produced by chords of the following types—
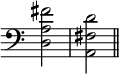
By playing these examples, the student will obtain some idea of the alteration which chords undergo in equal temperament. To understand it thoroughly, he should try the following simple experiment. 'Take an ordinary harmonium and tune two chords perfect on it. One is scarcely enough for comparison. To tune the triad of C major, first raise the G a very little, by scraping the end of the reed, till the Fifth, C—G, is dead in tune. Then flatten the Third E, by scraping the shank, till the triad C—E—G is dead in tune. Then flatten F till F—C is perfect, and A till F—A—C is perfect. The notes used are easily restored by tuning to their Octaves. The pure chords obtained by the above process offer a remarkable contrast to any other chords on the instrument.'[3] It is only by making oneself practically familiar with these facts, that the nature of temperament can be clearly understood, and its effects in the orchestra or in accompanied singing, properly appreciated.
Against its defects, equal temperament has one great advantage which specially adapts it to instruments with fixed tones, namely its extreme simplicity from a mechanical point of view. It is the only system of tuning which is complete with twelve notes to the Octave. This result is obtained in the following manner. If we start from any note on the keyboard (say G♭), and proceed along a series of twelve (tempered) Fifths upwards and seven Octaves downwards, thus—

we come to a note (F♯) identical with our original one (G♭). But this identity is only arrived at by each Fifth being tuned somewhat too flat for exact consonance. If, on the contrary, the Fifths were tuned perfect, the last note of the series (F♯) would be sharper than the first note (G♭) by a small interval called the 'Comma of Pythagoras,' which is about one-quarter of a Semitone. Hence in equal temperament, each Fifth ought to be made flat by one-twelfth of this Comma; but it is extremely difficult to accomplish this practically, and the error is always found to be greater in some Fifths than in others. If the theoretic conditions which the name 'equal temperament' implies, could be realised in the tuning of instruments, the Octave would be equally divided into twelve Semitones, six Tones, or three Major Thirds. Perfect accuracy, indeed, is impossible even with the best-trained ears, but the following rule, given by Mr. Ellis, is much less variable in its results than the ordinary process of guesswork. It is this:—'make all the Fifths which lie entirely within the Octave middle c′ to treble c″ beat once per second; and make those which have their upper notes above treble c″ beat three times in two seconds. Keeping the Fifth treble f′ and treble c″ to the last, it should beat once in between one and two seconds.'[4] In ordinary practice, however, much rougher approximations are found sufficient.
The present system of tuning, by equal temperament, was introduced into England at a comparatively recent date. In 1854 organs built and tuned by this method were sent out for the first time by Messrs. Gray & Davison, Walker, and Willis. 1854 is therefore the date of its definite adoption as the trade usage in England. There was no equally tempered organ of English make in the Great Exhibition of 1851; and before that time the present system appears to have been only used in a few isolated cases, as in the organ of S. Nicholas, Newcastle-upon-Tyne, which was retuned in 1842. For the pianoforte equal temperament came into use somewhat earlier than for the organ. It was introduced into the works of Messrs. Broadwood about 1846. In France the change had already taken place, for M. Aristide Cavaillé-Coll states that since 1835 he has consistently laboured to carry out the equal principle in the tuning of his organs.[5] What little is known of the history of temperament in Germany, seems to show that the new tuning was employed there at a still earlier date, but there are reasons for believing that equally tuned organs had not become general even as late as the time of Mozart (died 1791). Emanuel Bach seems to have been the first musician who advocated in a prominent manner the adoption of equal temperament, whence we may infer that it was unusual in his day.[6] His father is also said to have enployed this system on his own clavichord and harpsichord: but even his authority was not sufficient to recommend it to his contemporary Silbermann, the famous organ-builder (1683–1753). An earlier builder, Schnitger, is said to have used something approaching it in the organ built by him about 1688–93, in the S. Jacobi Church at Hamburg. Before that time the system appears to have had hardly more than a theoretic existence in Europe.[7]
The mode of tuning which prevailed before the introduction of equal temperament, is called the Meantone System.[8] It has hardly yet died out in England, for it may still be heard on a few organs in country churches. According to Don B. Yñiguez, organist of Seville Cathedral, the meantone system is generally maintained on Spanish organs, even at the present day.[7] Till about a century ago, this tuning, or a closely allied variety, was almost universally employed, both in England and on the Continent. It was invented by the Spanish musician Salinas, who was born at Burgos in 1513, lived for many years in Italy, and died at Salamanca in 1590.[9] On account of its historical interest, as well as its intrinsic merits, the meantone system requires a short explanation. It will be convenient to take equal temperament as the standard of comparison, and to measure the meantone intervals by the number of equal Semitones they contain. The relations of the two systems may therefore be described as follows.
If we start from say D on the keyboard, and proceed along a series of four equal temperament Fifths upwards and two Octaves downwards, thus—

we arrive at a note (F♯) which we employ as the Major Third of our original note (D). This tempered interval (D—F♯) is too sharp for exact consonance by nearly one-seventh of a Semitone; but if we make these Fifths flatter than they would be in equal temperament, then the interval D—F♯ will approach the perfect Major Third. We may thus obtain a number of systems of tuning according to the precise amount of flattening we choose to assign to the Fifth. Of this class the most important is the Meantone System, which is tuned according to the following rule. First, make the Major Third (say D—F♯) perfect; then make all the intermediate Fifths (D—A—E—B—F♯) equally flat by trial. After a little practice this can be done by mere estimation of the ear; but if very accurate results are desired, the following method may be used. A set of tuning forks should be made (say at French pitch) giving c′ = 260.2, g′ = 389.1, d′ = 290.9, a′ = 435 vibrations per second. The notes c′, g′, d′, a′, of the instrument should be tuned in unison with the forks, and all other notes can be obtained by perfect Major Thirds and perfect Octaves above or below these.
There is one difficulty connected with the use of the meantone system, namely that it requires more than twelve notes to the Octave, in order to enable the player to modulate into any given key. This arises from the nature of the system; for as twelve meantone Fifths fall short of seven Octaves, the same sound cannot serve both for G♭ and for F♯. Hence if we tune the following series of meantone Fifths
E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯
on the piano, or on any other instrument with twelve notes to the Octave, we shall have only six Major scales (B♭, F, C, G, D, A), and three Minor scales (G, D, A). When the remoter keys are required, the player has to strike G♯ instead of A♭, or E♭ instead of D♯, producing an intolerable effect. For in the meantone system the interval G♯—E♭ is sharper than the perfect Fifth by nearly one-third of a Semitone, and the four intervals B—E♭, F♯—B♭, C♯—F, G♯—C, are each sharper than the perfect Major Third by more than three-fifths of a Semitone. The extreme roughness of these chords caused them to be compared to the howling of wolves. [Wolf.]
To get rid of the 'wolves' many plans were tried. For instance, the G♯ was sometimes raised till it stood half-way between G and A; but the result was unsatisfactory, for the error thus avoided in one place had to be distributed elsewhere. This was called the method of Unequal Temperament, in which the notes played by the white keys were left in the meantone system, while the error was accumulated on those played by the black keys. The more usual scales were thus kept tolerably in tune, while the remote ones were all more or less false. Such a makeshift as this could not be expected to succeed, and the only purpose it served was to prepare the way for the adoption of equal temperament.
The meantone system is sometimes described as an 'unequal temperament,' but wrongly, since in it the so-called 'good keys' are all equally good; the 'bad keys' are simply those for which the necessary notes do not exist when the system is limited to twelve notes per Octave. The defect therefore lies not in the system itself, but in its application, and the only legitimate remedy is to increase the number of notes, and so provide a more extended series of Fifths. This was well understood from the first, for we find that as early as the 16th century many organs were constructed with extra notes.[10] Salinas tells us that he had himself played on one in the Dominican Monastery of Santa Maria Novella at Florence. Similar improvements were attempted in England. In the deed of sale of the organ built by Father Smith in 1682–3 for the Temple Church, London, special mention is made of the additional notes, which were played in the following manner:—two of the black keys were divided crosswise; the front halves, which were of the usual height, playing G♯ and E♭; the back ones, which rose above them, A♭ and D♯. About 1865, this organ was tuned for the first time in equal temperament, but the extra keys were not removed till 1878. The same method was followed in designing another organ of Father Smith's, which was built for Durham Cathedral in 1684–5, although the additional notes do not appear to have been actually supplied till 1691.[11] A different but equally ingenious plan of controlling the extra notes was used in the organ of the Foundling Hospital, London.[12] Here the keyboard was of the ordinary form, without any extra keys; but by means of a special mechanism four additional notes, D♭, A♭, D♯, A♯, could be substituted at pleasure for C♯, G♯, E♭, B♭ of the usual series. Close to the draw-stops on either side there was a handle or lever working in a horizontal cutting, and having three places of rest. When both handles were in the mid position, the series of notes was the same as on an ordinary instrument, namely
E♭-B♭-F-C-G-D-A-E-B-F♯-C♯-G♯;
but when the handles on both sides were moved in the outward direction, the E♭ and B♭ pipes were shut off, and the D♯ and A♯ were brought into operation. The use of this mechanism was afterwards misunderstood; the levers were nailed up for many years, and at last removed in 1848; but the tuning remained unaltered till 1855, when the organ itself was removed and a new one built in its place. The history of the old organ just described is of special interest, as bearing on Handel's position with reference to the question of temperament. Unfortunately all that we can now ascertain on the subject amounts to this:—that Handel presented an organ to the Hospital; that he performed on it at the opening ceremony on May 1, 1750;[13] and that it was still in existence in 1785.[14] We first hear of the extra notes in 1799,[15] but there is nothing to show that they did not belong to the original instrument given by Handel half a century before. Assuming this to have been the case, it would tend to show that the great composer was not in favour of abolishing the meantone system, but of remedying the defective form in which it was then employed. His example, and that of Father Smith, found few imitators, and those who did attempt to solve the problem seem often to have misunderstood its nature.[16] The difficulty however could not be shirked; for the development of modern music brought the remote keys more and more into common use; and as instruments continued to be made with only twelve notes per Octave, the only possible way to get rid of the 'wolves' was to adopt equal temperament.
The long contest between the different systems of tuning having practically come to an end, we are in a position to estimate what we have gained or lost by the change. The chief advantage of equal temperament is that it provides keyed instruments with unlimited facility of modulation, and places them, in this respect, more on a level with the voice, violin and trombone. It has thus assisted in the formation of a style of composition and execution suited to the pianoforte. It is the only system of intonation which, in concerted music, can be produced with the same degree of accuracy on every kind of instrument. Its deviations from exact consonance, though considerable, can be concealed by means of unsustained harmony, rapid movement, and soft quality of tone, so that many ears never perceive them. By constantly listening to the equally tempered scale, the ear may be brought not only to tolerate its intervals, but to prefer them to those of any other system, at least as far as melody is concerned. It has proved capable of being applied even to music of a high order, and its adoption may be considered an artistic success. From a commercial point of view, the change has been highly advantageous. It has enabled the maker of the pianoforte or the organ to obviate a serious imperfection without disturbing the traditional structure of the instrument; while, on the other hand, alterations both in the internal mechanism and in the form of keyboard would have been necessary if musicians had insisted that the 'wolves' should be got rid of without abolishing the old tuning. Trade usage will, therefore, be strongly on the side of equal temperament for a long time to come, and any attempt to recover the meantone system can only be made on a small scale, and for special purposes. Still, as many writers have pointed out, such a limited restoration would be useful. It would enable us to hear the music of the earlier composers as they heard it themselves. The ecclesiastical compositions of Bach, and all the works of Handel and his predecessors as far back as the 16th century, were written for the meantone system. By performing them in equal temperament we fail to realise the original intention. This would not be matter for regret if the old music were improved by our alteration; but such is certainly not the case. The tuning in which the old composers worked is far more harmonious than that which has replaced it. This much is generally admitted even by those who do not favour any attempt to restore the meantone system. They sometimes appeal to the authority of Sebastian Bach, and quote his approval of equal temperament as a reason why no other tuning should be used. But in reality very little is certainly known of Bach's relations to the subject. We are told that he was accustomed to tune his own clavichord and harpsichord equally, though the organ still remained in the meantone system. This statement is borne out by internal evidence. In Bach's organ works the remoter keys are scarcely ever employed, while no such restrictions are observable in his works for the clavichord. With his preference for a wide range of modulation he would naturally find the limits of the old-fashioned meantone organ irritating, and we can easily understand that he would have favoured any tuning which made all the keys available. He would doubtless have welcomed any practical method of extending the meantone system; but to provide this was a task beyond the inventive capacity of that age. His authority, then, may fairly be quoted to show that all the keys must be in tune to the same degree; but this condition can be realised by many other systems besides temperament when a sufficient number of notes is provided in each Octave. If the question were to be decided by an appeal to authority alone, we might quote the names of many musicians of last century who were acquainted with both kinds of temperament, and whose judgment was directly opposed to that of Bach. But this style of argument, always inconclusive, will appear peculiarly out of place when we consider what changes music has passed through since Bach's day. That the defects of equal temperament were not so noticeable then as now, may be attributed both to the different kind of instrument and the different style of composition which have since been developed. The clavichord which is said to have been an especial favourite with Bach, was characterised by a much softer quality of tone, and feebler intensity, than the modern pianoforte.[17] Again, composers of a century and a half ago relied for effect chiefly on vigorous counterpoint or skilful imitation between the various melodic parts, and not on the thick chords and sustained harmonies which have become so marked a feature in modern music. Owing to these changed conditions the evils of temperament are greatly intensified nowadays, and the necessity for some remedy has become imperative. There is but one direction in which an efficient remedy can be found, namely in the use of some more harmonious form of intonation than that which at present prevails. It is only by the help of an instrument on which the improved systems of tuning can be employed in an adequate manner, that the student will be able to estimate their value. Such an instrument we will now proceed to describe.
If we wish to employ any other system of tuning than equal temperament, we must increase the number of notes per Octave, since the ordinary twelve notes, unless tuned equally, are useless for anything beyond illustration or experiment. The methods used by Father Smith and by Handel cannot be followed nowadays. The ordinary keyboard is already so unsymmetrical, that the insertion of a few additional black or white keys would make it almost unplayable; and the changing of levers would be a troublesome interruption of the performance. The only way to bring the improved systems of temperament within the range of practical music, is to remodel and simplify the keyboard. This has been done in different ways by several inventors of late years. At a meeting of the Musical Association of London on May 1, 1875, an organ on which one of the stops was tuned according to the meantone system was exhibited by Mr. R. H. M. Bosanquet, of S. John's College, Oxford. The keyboard of this instrument—which is now in the South Kensington Museum—is arranged symmetrically, so that notes occupying the same relative position always make the same musical interval. There are twelve finger keys in the Octave, of which seven as usual are white and five black. The distance across from any key to its Octave, centre to centre, is six inches; each key is three-eighths of an inch broad, and is separated on either side from the next key by the space of one-eighth of an inch. As the Octave is the only interval in which all systems of intonation agree, keys an Octave apart are on the same level with each other. The rest of the keys are placed at various points higher or lower to correspond with the deviations of the pitch of their notes from equal temperament. Thus the G key is placed a quarter of an inch farther back, and one-twelfth of an inch higher than the C. The D key recedes and rises to the same extent relatively to the G, and so with the rest. After twelve Fifths we come to the B♯ key, and find it three inches behind and one inch above the from which we started. This oblique arrangement enables us to greatly increase the number of notes per Octave without any inconvenience to the player. At the same time the fingering is greatly simplified, for any given chord or scale always has the same form under the hand, at whatever actual pitch it may be played. Nor is it necessary to decide beforehand on the exact key-relationship of the passage, as it will be played in the same manner, whatever view may be taken of its analysis. The advantage of having thus to learn only one style of fingering for the Major scale, instead of twelve different styles, as on the ordinary keyboard, is self-evident. Chromatic notes are played according to the following rule:—put the finger up for a sharp and down for a flat. This results from the principle on which the keyboard is arranged, the higher keys corresponding to notes which are reached by an upward series of Fifths, and the lower keys to notes reached by a downward series. The following diagram shows the positions of the notes on the keyboard when applied to the meantone system:—
| • | • | • | • | • | e♯ | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | a♯ | • | • |
| • | • | • | d♯ | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | g♯ | • | • | • | • |
| • | c♯ | • | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | f♯ | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | • | b | • |
| • | • | • | • | e | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | a | • | • | • |
| • | • | d | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | g | • | • | • | • | • |
| c | • | • | • | • | • | • | • | • | • | • | • | c |
| • | • | • | • | • | f | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | b♭ | • | • |
| • | • | • | e♭ | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | a♭ | • | • | • | • |
| • | d♭ | • | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | g♭ | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | • | c♭ | • |
| • | • | • | • | f♭ | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | b♭♭ | • | • | • |
| • | • | e♭♭ | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | a♭♭ | • | • | • | • | • |
| d♭♭ | • | • | • | • | • | • | • | • | • | • | • | d♭♭ |
As all proposed improvements, either in music or anything else, are sure to meet with opposition, we will here consider some of the objections which may be made to the use of an instrument such as we have just described. It is natural that the new form of keyboard should be received with some hesitation, and that its style of fingering should be thought difficult; but in fact the old keyboard is far from being a model of simplicity, and many attempts have been made to reform it, independently of any aim at improving the tuning. [See Key, vol. ii. pp. 54, 55.] On the new keyboard the fingering is of the simplest possible character, and permits the attainment of any required rate of speed. All desirable combinations lie within easy grasp related notes being nearly on the same level. To prove that ordinary music can be easily adapted to the meantone organ, Mr. Bosanquet performed on it three of Bach's preludes at the meeting of the Musical Association already referred to. There would be no difficulty in constructing this form of keyboard with several manuals, nor in applying the same symmetrical arrangement to a pedal.
The advantage gained by employing an improved system of tuning depends so much on the quality of tone of the instrument, that it is very doubtful whether it would be worth while to adopt the meantone system for the pianoforte. It is only on the modern 'concert-grand' that the defects of equal temperament are felt to any great extent, and it might therefore be well to construct these instruments with a complete meantone scale. Still, the result would hardly be so satisfactory as on the organ, whether used in solo performance or in leading the voices of a choir.
The last objection which has to be considered is that enharmonic changes are supposed by some to be impossible in any system of tuning which provides distinct sounds for G♭ and F♯. This view is incorrect, as we shall recognise if we enquire what enharmonic changes really are. For the most part they are merely nominal, being used to avoid the strange appearance of remote keys. Thus in the 'Pro Peccatis' of Rossini's 'Stabat Mater,' there is apparently an enharmonic modulation from the key of A♮ to that of D♭.

But in reality it is a chromatic modulation from A♮ to C♯, with no enharmonic element whatsoever. The passage would be played on a meantone instrument as follows:—

It would be unnecessary in general to translate passages of this kind into correct notation before performing them, as in most cases the key-relations would be tolerably clear, in whatever way they were written. Should there be any chance of error in taking the accidentals literally, a large acute or grave mark might be drawn across the staff, to indicate that the notes are to be played twelve Fifths higher or lower than they are written. In the present instance, the acute mark could be used.
Sometimes the enharmonic change is real, and not merely a device of notation. Take the following extract from 'The people shall hear' in the 'Israel in Egypt':—

Here B♭ must be played in the second bar and A♯ in the third, a modulation which is rendered easy by the general construction of the passage. 'Enharmonic changes (Helmholtz remarks) are least observed when they are made immediately before or after strongly dissonant chords, or those of the Diminished Seventh. Such enharmonic changes of pitch are already sometimes clearly and intentionally made by violinists, and where they are suitable even produce a very good effect.'[18]
The necessity of avoiding 'wolves' in the meantone system sometimes restricts the choice of notes. Thus in a passage in the 'Lachrymosa' of Mozart's Requiem:—

the discord A♭—F—B♭—E♭ must be played exactly as it is written, owing to the B♭ and E♭ being prepared. Even if G♯ stood in the text, A♭ would be substituted in performance, as the 'wolf' G♯—E♭ is inadmissible. All such difficulties can be solved in a similar way. On the other side, we have to reckon the great variety of chords and resolutions which are available in the meantone system, but have no existence in equal temperament. Many chromatic chords may have two or more forms, such as the following:—

each of which may be used according to the key-relation of the context, or the effect required in the melodic parts. Again, the Augmented Sixth is much flatter in the meantone system than in equal temperament, slightly flatter even than the interval called the Harmonic Seventh. When the strange impression which it causes at first has worn off, its effect is peculiarly smooth and agreeable, especially in full chords. It is also available as Dominant Seventh, and may be written with the acute mark (G—/F), to distinguish it from the ordinary Minor Seventh got by two Fifths downwards (G—C—F).
It is important to recognise the fact that the forms of chords can only be settled by actual trial on an instrument, and that the judgment of the ear, after full experience of the different modes of tuning, cannot be set aside in favour of deductions from any abstract theory. Practice must first decide what chord or progression sounds best; and this being done, it may be worth while to ask whether theory can give any reasons for the ear's decision. In many cases our curiosity will be unsatisfied, but our preference for one effect rather than another will remain unchanged. Neither can theory solve those questions which sometimes arise as to the correct mode of writing certain chords. All questions of notation can only be decided by playing the disputed passage in some system of tuning which supplies a separate sound for each symbol. The reason why G♭ and F♯ were not written in the same chord was a purely practical one; these two signs originally meant different sounds, which formed combinations too rough for use. Our notation having been formed long before equal temperament came into use, it is not surprising that the symbols, do not correspond with the sounds. But they correspond exactly with the meantone scales, and it is on this system of tuning that all our rules of notation are founded. 'It is only necessary to remember that we have here the original system, which belongs from the very beginning of modern music onward to our musical notation, to see that by employing it we have the true interpretation of our notation; we have the actual sounds that our notation conveyed to Handel, to all before Bach, and many after him, only cured of the wolf, which was the consequence of their imperfect methods.'[19]
To carry out any system of temperament consistently in the orchestra is practically an impossible task. Tempered intervals can only be produced with certainty on a small number of the instruments, chiefly the wood-wind. The brass instruments have an intonation of their own, which differs widely from either of the temperaments we have described. Thus the French horn, whose notes are the harmonics arising from the subdivision of a tube, gives a Major Third much flatter than equal temperament, and a Fifth much sharper than the meantone system. [See Node; and Partial Tones.] There is necessarily a great deal of false harmony whenever the brass is prominently heard in tempered music. Again, the tuning of the string-quartet is accomplished by just Fifths (C—G—D—A—E), but as these instruments have free intonation, they can execute tempered intervals when supported by the pianoforte or organ. In the absence of such an accompaniment, both violinists and singers seem unable to produce equally tempered scales or chords. This is precisely what might have been expected on theoretic grounds, as the consonant relations of the different notes being partially lost through temperament, the altered intervals would naturally be difficult to seize and render. Fortunately, we have positive facts to prove the truth of this deduction. The subject has been recently investigated by two French savans, MM. Cornu and Mercadier.[20] Their experiments were made with three professional players, M. Léonard the Belgian violinist, M. Seligmann, violoncellist, and M. Ferrand, violinist of the Opéra Comique, besides amateur players and singers. The results showed that a wide distinction must be drawn between the intervals employed in unaccompanied melody, and those employed in harmony. In solo performances, continual variety of intonation was observed; the same pitch was seldom repeated, and even the Octave and the Fifth were sometimes sharpened or flattened. So far as any regularity could be traced, the intervals aimed at appeared to be those known as Pythagorean, of which the only consonant ones are the Octave, Fifth, and Fourth. The Pythagorean Major Third is obtained by four just Fifths up, and is consequently so sharp as to amount to a dissonance. In melody, a scale tuned in this manner is found to be not unpleasant, but it is impossible in harmony. This fact also was verified by Cornu and Mercadier, who report that, in two-part harmony, the players with whom they experimented invariably produced the intervals of just intonation. The Thirds and Sixths gave no beats, and the Minor Seventh on the Dominant was always taken in its smoothest form, namely the Harmonic Seventh. 'I have myself observed,' says Helmholtz, 'that singers accustomed to a pianoforte accompaniment, when they sang a simple melody to my justly intoned harmonium, sang natural Thirds and Sixths, not tempered, nor yet Pythagorean. I accompanied the commencement of the melody, and then paused while the singer gave the Third or Sixth of the key. After he had given it, I touched on the instrument the natural, or the Pythagorean, or the tempered interval. The first was always in unison with the singer, the others gave shrill beats.'2[21]
Since, then, players on bowed instruments as well as singers have a strong natural tendency towards just intervals in harmony, it is not clear why their instruction should be based on equal temperament, as has been the practice in recent times. This method is criticised by Helmholtz in the following words:—'The modern school of violin-playing, since the time of Spohr, aims especially at producing equally tempered intonation.… The sole exception which they allow is for double-stop passages, in which the notes have to be somewhat differently stopped from what they are when played alone. But this exception is decisive. In double-stop passages the individual player feels himself responsible for the harmoniousness of the interval, and it lies completely within his power to make it good or bad.… But it is clear that if individual players feel themselves obliged to distinguish the different values of the notes in the different consonances, there is no reason why the bad Thirds of the Pythagorean series of Fifths should be retained in quartet-playing. Chords of several parts, executed by a quartet, often sound very ill, even when each one of the performers is an excellent solo player; and, on the other hand, when quartets are played by finely cultivated artists, it is impossible to detect any false consonances. To my mind the only assignable reason for these results, is that practised violinists with a delicate sense of harmony, know how to stop the tones they want to hear, and hence do not submit to the rules of an imperfect school.'
Helmholtz found, by experiments with Herr Joachim, that this distinguished violinist in playing the unaccompanied scale, took the just and not the tempered intervals. He further observes that, 'if the best players, who are thoroughly acquainted with what they are playing, are able to overcome the defects of their school and of the tempered system, it would certainly wonderfully smooth the path of performers of the second order, in their attempts to attain a perfect ensemble, if they had been accustomed from the first to play scales by natural intervals.'
The same considerations apply to vocal music. 'In singing, the pitch can be made most easily and perfectly to follow the wishes of a fine musical ear. Hence all music began with singing, and singing will always remain the true and natural school of all music.… But where are our singers to learn just intonation, and make their ears sensitive for perfect chords? They are from the first taught to sing to the equally tempered pianoforte.… Correct intonation in singing is so far above all others the first condition of beauty, that a song when sung in correct intonation even by a weak and unpractised voice always sounds agreeable, whereas the richest and most practised voice offends the hearer when it sings false or sharpens.… The instruction of our present singers by means of tempered instruments is unsatisfactory, but those who possess good musical talents are ultimately able by their own practice to strike out the right path for themselves, and overcome the error of their original instruction.… Sustained tones are preferable as an accompaniment, because the singer himself can immediately hear the beats between the instrument and his voice, when he alters the pitch slightly.… When we require a delicate use of the muscles of any part of the human body, as, in this case, of the larynx, there must be some sure means of ascertaining whether success has been attained. Now the presence or absence of beats gives such a means of detecting success or failure when a voice is accompanied by sustained chords in just intonation. But tempered chords which produce beats of their own, are necessarily quite unsuited for such a purpose.'[22]
For performance in just intonation the three quartets of voices, strings, and trombones have a pre-eminent value; but as it requires great practice and skill to control the endless variations of pitch they supply, we are obliged to have some fixed and reliable standard by which they can at first be guided. We must be certain of obtaining with ease and accuracy any note we desire, and of sustaining it for any length of time. Hence we come back once more to keyed instruments, which do not present this difficulty of execution and uncertainty of intonation. The only question is how to construct such instruments with an adequate number of notes, if all the intervals are to be in perfect tune. Theoretically it is necessary that every note on the keyboard should be furnished with its Fifth, Major Third, and Harmonic Seventh, upwards and downwards. There should be Fifths to the Fifths, Thirds to the Thirds, and Sevenths to the Sevenths, almost to an unlimited extent. Practically these conditions cannot be fully carried out, and all instruments hitherto constructed in just intonation have been provided with material for the simpler modulations only. One of the best-known historical examples is General Perronet Thompson's organ, now in the collection of instruments in the South Kensington Museum. In each Octave this organ has forty sounds, which may be divided into five series, the sounds of each series proceeding by perfect Fifths, and being related to those of the next series by perfect Major Thirds. The interval of the Harmonic Seventh is not given. With a regular and consistent form of keyboard it would have been more successful than it was, but the idea of arranging the keys symmetrically had not then been developed. The first application of this idea was made by an American, Mr. H. W. Poole, of South Danvers, Massachusetts. His invention is described and illustrated in 'Silliman's Journal' for July, 1867. The principle of it is that keys standing in a similar position with regard to each other shall always produce the same musical interval, provided it occurs in the same relation of tonality. But if this relation of tonality alters, the same interval will take a different form on the keyboard. There are five series of notes, each proceeding by perfect Fifths:—(1) the keynotes; (2) the Major Thirds to the keynotes; (3) the Thirds to the Thirds; (4) the Harmonic Sevenths to the keynotes; (5) the Sevenths to the Thirds. The Major Thirds below the keynotes, which are so often required in modern music, as for instance in the theme of Beethoven's Andante in F, are not given. So that the range of modulation, though extensive, is insufficient for general purposes.[23]
Owing to the limited number of notes which keyed instruments can furnish, the attempt to provide perfect intervals in all keys is regarded by Helmholtz as impracticable. He therefore proposes a system of temperament which approaches just intonation so closely as to be indistinguishable from it in ordinary performance. This system is founded on the following facts:—We saw that in equal temperament the Fifth is too flat for exact consonance, and the Major Third much too sharp. Also that the interval got by four Fifths up (D—A—E—B—F♯) is identified with the Major Third (D—F♯).[24] Now if we raise the Fifths, and tune them perfectly, the interval D—F♯ becomes unbearable, being sharper than the equal temperament Third. But in a downward series of just Fifths the pitch becomes at each step lower than in equal temperament, and when we reach G♭, which is eight Fifths below D, we find that it is very nearly identical with the just Major Third of D, thus—

The best way of applying this fact is to tune a series of eight notes by just Fifths—say D♭, A♭, E♭, B♭, F, C, G, D; then a similar series forming just Major Thirds with these; whence it will result that the last note of the latter series (F♯) will form an almost exact Fifth with the first note of the former series (D♭).[25]
In applying the ordinary musical notation to systems of temperament of this class, a difficulty arises; for the Major Third being got by eight Fifths downward, would strictly have to be written D—G♭. As this is both inconvenient and contrary to musical usage, the Major Third may still be written D—F♯, but to distinguish this F♯ from the note got by four Fifths up, the following convention may be used. The symbols G♭ and F♯ are taken to mean exactly the same thing, namely the note which is eight Fifths below D. We assume G♭—D♭—A♭—E♭—B♭—F—C—G—D—A—E—B as a normal or standard series of Fifths. The Fifth of B is written indifferently /Gb or /F♯, the acute mark (/) serving to show that the note we mean belongs to the upward, and not to the downward series. The Fifth of /F♯ is written /C♯, and so on till we arrive at /B, the Fifth of which is written //F♯. In like manner, proceeding along a downward series, the Fifth below F♯ (or G♭) is written \B, and so on till we arrive at \F♯, the Fifth below which is written \\B. The notes B, E, A, D have their Thirds in the same series as themselves, thus D—F♯, \D—\F♯. Other notes have their Thirds in the series next below, thus C—\E, \C—\\E. These marks may be collected at the signature, like sharps and flats. The keys of A and E will be unmarked; the key of C will have three grave notes, \A, \E, \B. When it is necessary to counteract the grave or acute mark and restore the normal note, a small circle (o) may be prefixed, analogous to the ordinary natural.
To apply this mode of tuning to the organ would be expensive without any great advantages in return. Ordinary organ-tone, except in the reed and mixture stops, is too smooth to distinguish sharply between consonance and dissonance, and the pipes are so liable to the influence of heat and cold that attempts to regulate tile pitch minutely are seldom successful. Still less would it be worth while to tune the pianoforte justly. It is chiefly to the orchestra that we must look for the development of just intonation; but among keyboard instruments the most suitable for the purpose is the harmonium, which is specially useful as a means of studying the effects obtainable from untempered chords.
| • | • | • | • | • | /f | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | /a♭ | • | • |
| • | • | • | /e♭ | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | /a♭ | • | • | • | • |
| • | /d♭ | • | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | /g♭ | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | • | b | • |
| • | • | • | • | e | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | a | • | • | • |
| • | • | d | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | g | • | • | • | • | • |
| c | • | • | • | • | • | • | • | • | • | • | • | c |
| • | • | • | • | • | f | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | b♭ | • | • |
| • | • | • | e♭ | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | a♭ | • | • | • | • |
| • | d♭ | • | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | g♭ | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | • | • | \b | • |
| • | • | • | • | \e | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | • | • | \a | • | • | • |
| • | • | \d | • | • | • | • | • | • | • | • | • | • |
| • | • | • | • | • | • | • | \g | • | • | • | • | • |
| \c | • | • | • | • | • | • | • | • | • | • | • | \c |
There is in the South Kensington Museum a harmonium, the tuning of which may be considered identical with the system just explained. The form of keyboard is that which has already been described in connexion with the meantone temperament; and it is equally applicable to the system of perfect Fifths. Being an experimental instrument it was constructed with eighty-four keys in each Octave, but for ordinary purposes it is found that about half that number would be sufficient. The fingering of the Major scale resembles that of A♭ Major on the ordinary keyboard, and is always the same, from whatever note we start as Tonic. Moreover the form which any given chord takes does not depend on theories of tonality, but is everywhere symmetrical. The diagram in the preceding column shows the positions of the notes on the keyboard when applied to the system of perfect Fifths.
It is unnecessary to consider here the objections which might be made to the use of this tuning, as they would, no doubt, be similar to those we have already noticed in dealing with the meantone temperament. But it may be pointed out that the supposed difficulty of enharmonic change no more exists here than elsewhere. We may even modulate through a series of eight Fifths down, and return by a Major Third down, without altering the pitch. The following passage from a madrigal, 'O voi che sospirate,' by Luca Marenzio (died 1590) illustrates this:
A musical score should appear at this position in the text. See Help:Sheet music for formatting instructions |
In the 4th bar G♯ and C♯ are written for A♭ and D♭; and in the 5th bar F♯, \B and D for G♭, \C♭, E♭♭, but the confused notation would not affect the mode of performance either with voices or the justly tuned harmonium.
The practical use of this instrument has brought to light certain difficulties in applying just intonation to ordinary music. The chief difficulty comes from the two forms of Supertonic which are always found in a perfectly tuned Major Scale. Thus, starting from C, and tuning two Fifths upwards (C—G—D) we get what might be considered the normal Supertonic (D); but by tuning a Fourth and a Major Sixth upwards (C—F—\D) we arrive at a flatter note, which might be called the grave Supertonic (\D). The first form will necessarily be employed in chords which contain the Dominant (G), the second form in chords which contain the Subdominant (F) or the Superdominant (\A). Otherwise, false Fifths or Fourths (G—\D; D—\A) would be heard. The result is that certain chords and progressions are unsuitable for music which is to be performed in perfect tuning. Let us take the following example and arrange it in its four possible forms:—
A musical score should appear at this position in the text. See Help:Sheet music for formatting instructions |
All of these are equally inadmissible; No. 1 being excluded by the false Thirds (F—A; A—C); No. 2 by the false Fourth (\A—D); No. 3 by the false Fifth (G—\D); No. 4 by the sudden fall of the pitch of the tonic. If this kind of progression is employed, all the advantages of just intonation are lost, for the choice only lies between mistuned intervals and an abrupt depression or elevation of the general pitch.
The idea of writing music specially to suit different kinds of temperament is a somewhat unfamiliar one, although, as already remarked, Bach employed a narrower range of modulation in his works for the meantone organ than in those for the equally tempered clavichord. The case has some analogy to that of the different instruments of the orchestra, each of which demands a special mode of treatment, in accordance with its capabilities. The same style of writing will evidently not suit alike the violin, the trombone, and the harp. In the same way, just intonation differs in many important features both from the equal and from the meantone temperament; and before any one of these systems can be used with good effect in music, a practical knowledge of its peculiarities is indispensable. Such knowledge can only be gained with the help of a keyed instrument, and by approaching the subject in this manner, the student will soon discover for himself what modulations are available and suitable in perfect tuning. He will see that these restrictions are in no sense an invention of the theorist, but are a necessary consequence of the natural relations of sounds.
If just intonation does not permit the use of certain progressions which belong to other systems, it surpasses them all in the immense variety of material which it places within the composer's reach. In many cases it supplies two or more notes of different pitch where the ordinary temperament has but one. These alternative forms are specially useful in discords, enabling us to produce any required degree of roughness, or to avoid disagreeable changes of pitch. For instance, the Minor Seventh may be taken either as C—/B♭ (ten Fifths up), or as C—B♭ (two Fifths down), or as C—\B♭ (fourth Fifths down). When added to the triad C—\E—G, the acute Seventh, /B♭, is the roughest, and would be used if the Minor Third G—/B♭ should occur in the previous chord. The intermediate form, B♭, would be used when suspended to a chord containing F. The grave Seventh, \B♭, is the smoothest, being an approximation to the Harmonic Seventh. Many other discords, such as the triad of the Augmented Fifth and its inversions, may also be taken in several forms. But this variety of material is not the only merit of perfect tuning. One of the chief sources of musical effect is the contrast between the roughness of discords and the smoothness of concords. In equal temperament this contrast is greatly weakened, because nearly all the intervals which pass for consonant are in reality more or less dissonant. The loss which must result from this in the performance of the simpler styles of music on our tempered instruments, will be readily understood. On the other hand, in just intonation the distinction of consonance and dissonance is heard in its full force. The different inversions and distributions of the same chord, the change from Major to Minor Modes, the various diatonic, chromatic, and enharmonic progressions and resolutions have a peculiar richness and expressiveness when heard with untempered harmonies.
There is yet another advantage to be gained by studying the different kinds of tuning. We have seen that even in those parts of the world where equal temperament has been established as the trade usage, other systems are also employed. Many countries possess a popular or natural music, which exists independently of the conventional or fashionable style, and does not borrow its system of intonation from our tempered instruments. Among Oriental nations whose culture has come down from a remote antiquity, characteristic styles of music are found, which are unintelligible to the ordinary European, only acquainted with equal temperament. Hence transcriptions of Oriental music, given in books of travel, are justly received with extreme scepticism, unless the observer appears to be well acquainted with the principles of intonation and specifies the exact pitch of every note he transcribes. As illustrations of these remarks we may cite two well-known works on the history of the art, Kiesewetter's 'Musik der Araber,' and Villoteau's 'Musique en Égypte.' Both of these authors had access to valuable sources of information respecting the technical system of an ancient and interesting school of music. Both failed to turn their opportunities to any advantage. From the confused and contradictory statements of Kiesewetter only one fact can be gleaned, namely, that in the construction of the lute, the Persians and the Arabs of the Middle Age employed the approximately perfect Major Third, which is got by eight downward Fifths. From the work of Villoteau still less can be learnt, for he does not describe the native method of tuning, and he gives no clue to the elaborate musical notation in which he attempted to record a large number of Egyptian melodies. Yet it would have been easy to denote the oriental scales and melodies, so as to enable us to reproduce them with strict accuracy, had these authors possessed a practical knowledge of untempered intervals.
It may be useful, in concluding this article, to refer to some current misapprehensions on the subject of temperament. It is sometimes said that the improvement of intonation is a mere question of arithmetic, and that only a mathematician would object to equal tuning. To find fault with a series of sounds because they would be expressed by certain figures, is not the kind of fallacy one expects from a mathematician. In point of fact, equal temperament is itself the outcome of a mathematical discovery, and furnishes about the easiest known method of calculating intervals. Besides, the tenor of this article will show that the only defects of temperament worth considering are the injuries it causes to the quality of musical chords. Next, it is said that the differences between the three main systems of tuning are too slight to deserve attention, and that while we hear tempered intervals with the outward ear, our mind understands what are the true intervals which they represent. But if we put these theories to a practical test, they are at once seen to be unfounded. It has been proved by experiment that long and habitual use of equal temperament does react on the sense of hearing, and that musicians who have spent many years at the keyboard have a dislike to just chords and still more to just scales. The Major Sixth is specially objected to, as differing widely from equal temperament. This feeling is so entirely the result of habit and training, that those who are not much accustomed to listen to keyed instruments do not share these objections, and even equally tempered ears come at last to relish just intervals. We may infer, then, that the contrast between the various kinds of intonation is considerable, and that the merits of each would be easily appreciated by ordinary ears. And although the student may, at first, be unable to perceive the errors of equal temperament or be only vaguely conscious of them, yet by following out the methods detailed above, he will soon be able to realise them distinctly. It need not be inferred that equal temperament is unfit for musical purposes, or that it ought to be abolished. To introduce something new is hardly the same as to destroy something old. An improved system of tuning would only be employed as an occasional relief from the monotony of equal temperament, by no means as a universal substitute. The two could not, of course, be heard together; but each might be used in a different place or at a different time. Lastly, it is said that to divide the scale into smaller intervals than a Semitone is useless. Even if this were true, it would be irrelevant. The main object of improved tuning is to diminish the error of the tempered consonances: the subdivision of the Semitone is an indirect result of this, but is not proposed as an end in itself. Whether the minuter intervals would ever be useful in melody is a question which experience alone can decide. It rests with the composer to apply the material of mean and just intonation, with which he is now provided. The possibility of obtaining perfect tuning with keyed instruments is one result of the recent great advance in musical science, the influence of which seems likely to be felt in no branch of the art more than in Temperament.[ J. L. ]
- ↑ Some theorists exclude the Harmonic Seventh from the list of elementary intervals, but it is often heard in unaccompanied vocal harmony. See below, p. 77a.
- ↑ Those who wish to study the subject more in detail may consult:—(1) Bosanquet, 'Elementary Treatise on Musical Intervals and Temperament' (Macmillan); (2) Helmholtz, 'Sensations of Tone,' chapters xiv. to xvii.; and Ellis's Appendix xix. sections A to G, tables i. to vi.: (3) Perronet Thompson, 'On the Principles and Practice of Just Intonation': (4) Woolhouse, 'Essay on Musical Intervals.'
- ↑ Bosanquet, 'Temperament,' p. 6
- ↑ Ibid. p. 5.
- ↑ Ellis, in Nature for Aug. 8, 1878, p. 383.
- ↑ C. P. E. Bach, 'Versuch über die wahre Art das Clavier zu spielen, Einleitung, sect. 14; published 1753.
- ↑ 7.0 7.1 Ellis, 'History of Musical Pitch,' in Journal of Society of Arts, March 5 and April 2, 1880, and Jan. 7, 1881. From these valuable papers many of the facts given in the text have been derived.
- ↑ Otherwise Mesotonic; so called because in this tuning the Tone is a mean between the Major and the Minor Tones of Just Intonation; or half a Major Third. See p. 79b.
- ↑ The invention of this temperament has also been attributed to Zarlino and to Guido d'Arezzo.
- ↑ The extra notes were sometimes called 'Quartertones,' not a very suitable name, since a Quartertone is not a sound, but an interval, and the Semitone is not divided equally in the meantone system.
- ↑ See vol. ii. p. 593, note.
- ↑ The history of this instrument has been carefully investigated by Mr. Alexander J. Ellis. F.R.S. The facts given in the text were derived by him from a MS. note-book made by Mr. Leffler (died 1819), organist of S. Katherine's (then by the Tower), and father of the singer William Leffler. [See vol. ii. p. 112.]
- ↑ Brownlow, 'History and Objects of the Foundling Hospital,' p. 78.
- ↑ Burney, 'Sketch of the life of Handel,' p. 28, prefixed to 'Account of the Commemoration.'
- ↑ See remarks by an anonymous writer in 'The European Magazine,' for Feb. 1799, who, however, states (1) that the organ with extra notes was not given by Handel, and (2) that it was built under the direction of Dr. Robert Smith, Master of Trinity College, Cambridge. The contradiction between this writer and Burney might be removed by supposing that a new instrument was built between 1785 and 1799; but of this we have no record. If the extra notes were designed by Dr. Smith, It must have been before 1768, as he died in that year, aged 79. In 1762 he had published a 'Postscript' to his treatise on 'Harmonics,' recommending an arrangement of stops by which a meantone series of nineteen notes to the Octave (Db to F##) could be played with the ordinary keyboard. He had this plan carried out in a harpsichord constructed by Kirkman.
- ↑ See account of Renatus Harris's Invention, Hopkins, 'The Organ, in Rimbault's 'History of the Organ,' pp. 121, 122.
- ↑ Bosanquet. 'Temperament,' pp. 28, 29.
- ↑ 'Sensations of Tone,' p. 513.
- ↑ Bosauquet, 'Temperament,' p. 39.
- ↑ See Ellis's Appendix to the 'Sensations of Tone,' p. 787.
- ↑ 'Sensations of Tone,' p. 640.
- ↑ 'Sensations of Tone,' pp. 505–510.
- ↑ The keyboard invented by Mr. Colin Brown of Glasgow, is similar in principle to Mr. Poole's, except that it does not give the two series of Harmonic Sevenths. See Bosanquet, 'Temperament.'
- ↑ In general when a series of Fifths is compared with a Major Third, the number of Octaves (by which we must ascend or descend in order to bring the notes into the same part of the scale) is not expressed, but can be easily supplied by the reader.
- ↑ The error, which is called a 'Skhisma,' is about the fifty-first part of a Semitone. This system, therefore, differs so slightly from just intonation, that we shall henceforward treat them as practically identical.
