(25 ) and (26 ) may be written
(27 )
d
s
=
[
1
+
(
d
y
d
x
)
2
]
1
2
d
x
{\displaystyle ds=\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}dx}
(28 )
d
s
=
[
(
d
x
d
y
)
2
+
1
]
1
2
d
y
{\displaystyle ds=\left[\left({\frac {dx}{dy}}\right)^{2}+1\right]^{\frac {1}{2}}dy}
Substituting the value of ds from (27 ) in (26 ) ,
(29 )
cos
τ
=
1
[
1
+
(
d
y
d
x
)
2
]
1
2
,
sin
τ
=
d
y
d
x
[
1
+
(
d
y
d
x
)
2
]
1
2
{\displaystyle \cos \tau ={\frac {1}{\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}}},\ \sin \tau ={\frac {\frac {dy}{dx}}{\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}}}}
(24 ) -(26 ) differentials dx, dy, ds is to note that they are correctly represented by a right triangle whose hypotenuse is ds , whose sides are dx and dy , and whose angle at the base is
τ
{\displaystyle \tau }
d
s
=
(
d
x
)
2
+
(
d
y
)
2
,
{\displaystyle ds={\sqrt {(dx)^{2}+(dy)^{2}}},}
and, dividing by dx or dy , gives (24 ) or (25 ) respectively. Also, from the figure,
cos
τ
=
d
x
d
s
,
sin
τ
=
d
y
d
s
;
{\displaystyle \cos \tau ={\frac {dx}{ds}},\ \sin \tau ={\frac {dy}{ds}};}
the same relations given by (26 ) .
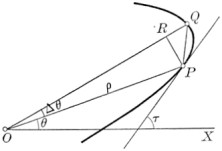
91. Derivative of the arc in polar coördinates. §67
PRQ
(
chord
P
Q
Y
)
2
{\displaystyle ({\mbox{chord}}PQY)^{2}}
=
(
P
R
)
2
+
(
R
Q
)
2
{\displaystyle =(PR)^{2}+(RQ)^{2}}
=
(
ρ
sin
Δ
θ
)
2
+
(
ρ
+
Δ
ρ
−
ρ
cos
Δ
θ
)
2
{\displaystyle =(\rho \sin \Delta \theta )^{2}+(\rho +\Delta \rho -\rho \cos \Delta \theta )^{2}}
Dividing throughout by
(
Δ
θ
)
2
{\displaystyle (\Delta \theta )^{2}}
(
chord
P
Q
Δ
θ
)
2
=
ρ
2
(
sin
Δ
θ
Δ
θ
)
2
+
(
Δ
ρ
Δ
θ
+
ρ
⋅
1
−
cos
Δ
θ
Δ
θ
)
2
.
{\displaystyle \left({\frac {{\mbox{chord}}PQ}{\Delta \theta }}\right)^{2}=\rho ^{2}\left({\frac {\sin \Delta \theta }{\Delta \theta }}\right)^{2}+\left({\frac {\Delta \rho }{\Delta \theta }}+\rho \cdot {\frac {1-\cos \Delta \theta }{\Delta \theta }}\right)^{2}.}
![{\displaystyle ds=\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0be4d42393d62651fa28be2ebf16abbe3a7131f9)
![{\displaystyle ds=\left[\left({\frac {dx}{dy}}\right)^{2}+1\right]^{\frac {1}{2}}dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dd58b7d28b3cb4e49c802e7826e0702e0c3af92)
![{\displaystyle \cos \tau ={\frac {1}{\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}}},\ \sin \tau ={\frac {\frac {dy}{dx}}{\left[1+\left({\frac {dy}{dx}}\right)^{2}\right]^{\frac {1}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46ad62826e6b1181f896c6853666a9145512c9a5)
An easy way to remember the relations (24)-(26) differentials dx, dy, ds is to note that they are correctly represented by a right triangle whose hypotenuse is ds, whose sides are dx and dy, and whose angle at the base is . Then
From the right triangle PRQ
